
- •Содержание курса
- •Тема 1. Комбинаторика
- •§ 1. Перестановки, сочетания и размещения
- •§ 2. Перестановки, сочетания и размещения с повторениями
- •Тема 2. Теория вероятностей
- •§ 3. Случайные события. Понятия вероятности
- •§ 4. Теоремы сложения и умножения. Условная вероятность
- •§ 5. Формула полной вероятности
- •§ 6. Формула Байеса
- •§ 7. Формула Бернулли
- •Задачи на повторение
- •Тема 3. Случайные величины
- •§ 8. Дискретные и непрерывные величины.
- •§ 9. Функция распределения и плотность распределения вероятности
- •§ 10, 11. Математическое ожидание и дисперсия
- •§ 12. Мода и медиана
- •§ 13. Законы распределения:
- •Тема 4. Математическая статистика
- •§ 16. Статистическое распределение. Полигон и гистограмма
- •§ 17. Числовые характеристики выборки.
- •§ 18. Точечные и интервальные оценки
- •§ 19. Выравнивание частот
- •§ 20. Проверка гипотез о значениях числовых параметров:
- •§ 21. Критерий Пирсона
- •§ 22. Линейная корреляция
- •§ 23. Уравнение линии регрессии Литература
Содержание курса
Тема 1. Комбинаторика
§ 1. Перестановки, сочетания и размещения.
§ 2. Перестановки, сочетания и размещения с повторениями.
Тема 2. Теория вероятностей
§ 3. Случайные события. Понятия вероятности.
§ 4. Теоремы сложения и умножения. Условная вероятность.
§ 5. Формула полной вероятности.
§ 6. Формула Байеса.
§ 7. Формула Бернулли.
Тема 3. Случайные величины
§ 8. Дискретные и непрерывные величины.
§ 9. Функция распределения и плотность распределения вероятности.
§ 10. Математическое ожидание и его свойства.
§ 11. Дисперсия и её свойства.
§ 12. Мода и медиана.
§ 13. Законы распределения. Дискретные распределения: геометрическое, биномиальное, Пуассона. Непрерывные распределения: равномерное, нормальное, показательное.
§ 14. Средние величины: средняя арифметическая, средняя гармоническая, средняя квадратичная, средняя кубическая.
Тема 4. Математическая статистика
§ 15. Генеральная совокупность и выборка. Репрезентативность выборки.
§ 16. Статистическое распределение. Полигон и гистограмма.
§ 17. Числовые характеристики выборки (выборочные средние, выборочная дисперсия, выборочная исправленная дисперсия). Эмпирическая функция распределения. Точечные оценки.
§ 18. Интервальные оценки.
§ 19. Выравнивание частот.
§ 20. Статистические гипотезы (основная и альтернативная гипотезы, простая и сложная гипотезы). Статистический критерий, критическая область допустимых значений критерия, уровень значимости, ошибки первого и второго рода.
§ 21. Проверка гипотез о значениях числовых параметров. F-критерий Фишера (для сравнения дисперсий) и t-критерий Стьюдента (для сравнения средних величин).
§ 22. Критерий Пирсона.
Тема 5. Элементы корреляционного и регрессионного анализа
§ 23. Функциональная зависимость и корреляция, коэффициент линейной корреляции, способы его вычисления и свойства.
§ 24. Корреляционное отношение, коэффициенты детерминации, оценка формы связи, коэффициент корреляции Фехнера, коэффициент корреляции Спирмена, коэффициент ассоциации..
§ 25. Понятие регрессии, уравнение линии регрессии, определение параметров линейной регрессии методом наименьших квадратов.
Тема 1. Комбинаторика
§ 1. Перестановки, сочетания и размещения
|
1. Сколькими способами 7 человек могут встать в очередь в кассу?
2. В финальной части первенства Европы по футболу участвуют 16 команд. Сколькими способами можно распределить золотую, серебряную и бронзовую медали?
3. Сколько шестизначных чисел кратных пяти можно составить из цифр 1,2,3,4,5,6 при условии, что в числе цифры не повторяются?
4. Хоккейная команда состоит из 2 вратарей, 7 защитников и 10 нападающих. Сколькими способами тренер может образовать шест ёрку из 1 вратаря, 2 защитников и 3 нападающих?
5. Сколько существует различных телефонных номеров из 7 цифр?
6. В 7-м классе изучают 14 предметов. Сколькими способами можно расставить расписание на субботу, если в этот день 5 разных уроков?
7. Из группы, состоящей из 7 мужчин и 4 женщин, надо выбрать 6 человек так, чтобы среди них было не менее 2 женщин?
8. Сколько различных перестановок можно образовать из букв слова «задача»?
9. Кубок по футболу разыгрывают 6 команд 1-й лиги и 10 команд 2-й лиги. Сколькими способами можно разбить все команды на две группы по 8 команд так, чтобы в каждой группе было по 3 команды 1-й лиги?
10. Сколько трёхзначных чисел можно составить из цифр 1,2,3,4,5?
11. Сколько трёхзначных чисел можно составить из цифр 1,2,3,4,5, если каждую цифру можно использовать не более одного раза?

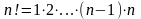
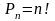 перестановка
n
элементов
перестановка
n
элементов
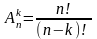 размещение
из n
элементов по k
(порядок важен!)
размещение
из n
элементов по k
(порядок важен!)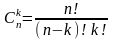 сочетание
из n
элементов по k
(порядок неважен!)
сочетание
из n
элементов по k
(порядок неважен!)