354

6. Модели исследования операций

Модели исследования операций решают специальные задачи на уровне предприятий и фирм.

Сетевые модели находят использование, когда необходимо упорядочить большой комплекс взаимосвязанных работ, определить график последовательности работ с указанием времени начала каждой работы. Как правило, такие модели востребованы в сфере строительства.

Модели системы массового обслуживания формируют информационную базу для выработки рекомендаций по рациональной организации обслуживания, например, оценить количество кассиров в течение дня, чтобы длина очереди была минимальной. Такого плана модели находят использование в сфере услуг [23].

Модели управления запасами используются для решения задач снабжения и позволяют определять оптимальные объемы поставок каждого вида материалов и временные сроки поставок. Потребность в такого рода моделях возникает в связи с необходимостью, с одной стороны бесперебойного снабжения материалами, с другой, - с тем, что необоснованное увеличение объема поставок требует не только дополнительных мер по хранению материалов, но и связана с проблемой замораживания капитала в виде запасов.

Модели теории игр используются в том случае, когда при определенных условиях экономической конъюнктуры из нескольких альтернатив решения должна быть выбрана та альтернатива, которая лучше всего способствует осуществлению цели. Основная сложность использования данного класса моделей состоит в ее информационном обеспечении: практически вся входная информация модели оценивается экспертно, поэтому достоверность модельных расчетов, полученных на данной информации, является достаточно условной.

Отметим, что все модели данного класса легко реализуемы с использованием таблицы Excel путем введения соответствующих моделям формул. Исключение составляют сетевые модели, практическая реализация которых требует специального пакета прикладных программ.

6.1. Модели сетевого планирования и управления

Метод сетевого планирования по сравнению с другими методами исследования операций относительно молод. Впервые он был использован в пятидесятых годах в США для составления план-графика строительных работ. Метод был основан на построении сетевых графиков и получил название метод критического пути, англоязычный вариант – Critical Path Method – CPM. В то же время в военно-морских силах США был создан метод анализа и оценки программ – PERT от Program evaluation and Review Technique. Впоследствии оба метода были объединены под общим названием PERT-CPM, русскоязычный вариант – метод сетевого планирования и управления (СПУ) [15]. К настоящему времени технология сетевого планирования и управления уже достаточно хорошо отлажена и отлично зарекомендовала себя в таких областях деятельности, как разработка и подготовка к производству новых видов изделий, строительство и реконструкция, проведение научно-исследовательских и опытно-конструкторских работ, разработка новых программных продуктов.

6.1.1. Основные принципы построения сетевой модели

Сетевые методы – это совокупность математических методов, в основе которых лежит графическое представление комплекса работ в виде сетевого графика (сети).

Таким образом, основным элементом систем СПУ является сетевая модель, которая моделирует процесс выполнения комплекса работ для достижения определенной цели (в дальнейшем комплекс работ для достижения определенной цели будем называть проектом). Графическое изображение сетевой модели называется сетевым графиком.

3

1

4

2

Рис. 6.1.1.

Сетевой график с математической точки зрения представляет собой ориентированный граф без петель и контуров. Обозначим его G = ( ), где Е – непустое конечное множество вершин, а – конечное множество ориентированных дуг, соединяющих некоторые пары вершин.

Дугам на сетевом графике соответствуют работы, а вершинам – события.

(в мировой практике встречается и другое представление: работы – вершины; события – дуги).

Работа – это любые действия, трудовые процессы, сопровождающиеся затратами времени или (и) ресурсов и приводящие к определенным результатам.

Все работы можно разделить на действительные работы, ожидания, фиктивные (зависимости). Под действительными работами следует понимать любой трудовой процесс, требующий ресурсов и имеющий некоторую продолжительность (на графике изображаются сплошными стрелками). Ожидание – это некоторый процесс, не требующий ресурсов, но имеющий некоторую продолжительность (на графике – штрих-пунктирными стрелками). Фиктивные работы (зависимости) не требуют ресурсов и имеют нулевую продолжительность, они используются для обозначения логических зависимостей между действительными работами (на графике изображаются пунктирными стрелками).

Событие – обозначает факт окончания работ, в него входящих или начала работ из него выходящих, оно не имеет продолжительности и не потребляет ресурсов. На графике изображается кружочками, квадратами или прямоугольниками. На любом сетевом графике можно выделить исходное, промежуточное и завершающее события.

Исходное событие указывает на факт начала выполнения всего комплекса работ, описываемого сетевой моделью. Оно не имеет предшествующих работ. Промежуточное событие представляет собой результат одной или нескольких работ, который обеспечивает возможность начать одну или несколько последующих работ. Завершающее событие указывает на факт достижения цели, т.е. окончания всего комплекса работ. Оно не имеет следующих за ним работ. Если оно одно, то сетевой график одноцелевой.

Событие выражает логическую связь между работами, заключающуюся в том, что работы, входящие в данное событие, непосредственно предшествуют работам, выходящим из него; ни одна, выходящая из данного события работа, не может начинаться до окончания всех работ, входящих в это событие.

Любая работа сетевой модели соединяет два события: начальное событие работы и конечное событие работы. Для однозначного обозначения работ используют идентификаторы (i, j), где i – номер начального события работы, j – номер конечного события работы. Обычно на сетевых графиках события упорядочены, то есть i < j.

Основой успешного построения сетевой модели является хорошее знание проекта и технологии выполнения работ. При этом используется ряд определенных правил и приемов.

Принципы построения сетевых графиков.

1. Как правило, последовательность работ изображается слева направо.

2. Если работы А и В выполняются последовательно:

2

3

А

В

Рис.6.1.2.

3. Если для выполнения работ А и В необходим результат работы С:

А

С

В

Рис.6.1.3

4. Е

   А

   сли для выполнения работы С требуется результат работ А и В

С

В

Рис. 6.1.4

5. Если работа С следует за двумя параллельно идущими работами А и В, а работа D только за работой В, то:

C

A

4

7

9

D

B

5

6

8

Рис. 6.1.5

6. Одноцелевые графики имеют одно начальное событие и одно конечное.

7. На сетевых графиках не должно быть тупиков, т.е. событий, из которых не выходит ни одна работа, кроме завершающего.

8. Не должно быть событий, которым на предшествует ни одна работа (кроме исходного).

9. Не должно быть замкнутых циклов (контуров), т.е. путей, соединяющих некоторые события с ними же самими.

Рис. 6.1.6

10. Два события не могут быть соединены более чем одной работой (петля). В этом случае рекомендуется ввести дополнительное событие и фиктивную работу.

2

Рис. 6.1.7

11. В сетевых моделях следует соблюдать определенную последовательность в нумерации событий от исходного к завершающему. События должны быть упорядочены по рангам, так как графики, у которых нумерация осуществлена по правилу i<j, очень удобны для анализа и проведения расчетов.

Для упорядочения вершин можно воспользоваться графическим способом (методом вычеркивания дуг).

1. Исходную вершину (в которую не входит ни одна дуга) отнесем к рангу 0 и присвоим ей номер 1.

2. Вычеркнем все дуги, выходящие из вершины 1. И отнесем события, оказавшиеся без входящих дуг, к первому рангу. Этим событиям присвоим в произвольном порядке номера 2, 3…k₁.

3. Вычеркнув все дуги, выходящие из вершин предыдущего ранга, отнесем вершины, оказавшиеся без входящих дуг, к следующему рангу и последовательно пронумеруем их. Этот шаг повторяем до тех пор, пока все вершины не будут пронумерованы. При этом получается, что события одного и того же ранга между собой не соединены работами, а события старших рангов имеют больший номер. Порядок нумерации событий одного и того же ранга может быть произвольным.

В случае необходимости упорядочения сетей большой размерности удобно пользоваться аналитическим методом – алгоритмом Форда.

Прежде чем представлять комплекс работ сетевым графиком, необходимо составить перечень работ, подлежащих выполнению, оценить продолжительность каждой работы (она может быть детерминированной либо определяться на основе вероятностных оценок) и установить последовательность выполнения работ. Такой перечень удобно представить в виде структурно - временной таблицы.

Рассмотрим пример.

Пример 6.1.1. Университет рассматривает предложение о строительстве нового корпуса. Работы, которые следует выполнить перед началом строительства, представлены в табл.

Таблица

Исходные данные примера 6.1.1

Работа	Содержание работы	Предшествующие работы	Продолжительность работ, нед.
А1 А2 А3 А4 А5 А6 А7 А8	Определить место строительства Разработать первоначальный проект Получить разрешение на строительство Выбрать архитектурную мастерскую Разработать смету затрат на строительство Закончить разработку проекта Получить финансовое обеспечение Нанять подрядчика	– А1 А1 А3 А3 А2,А4, А5 А2, А5 А6, А7	6 8 12 4 12 10 12 8

Требуется построить сетевой график проекта.

Решение.

4

А₇

А₂

А₈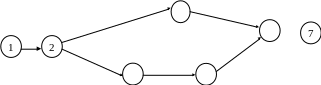

6

А₅

А₆

А₁

А₃

А₄

3

5

Рис. Сетевой график примера 6.1.1.

Работа А₁ не имеет предшествующих, поэтому изображается дугой, выходящей из события 1. Масштаб при этом не соблюдается. Работе А₂ предшествует работа А₁, поэтому дуга А₂ изображается на сетевом графике вслед за дугой А₁. А₃ изображается аналогично А₂. Далее надо изобразить работы А₄ и А₅, выполняющиеся после работы А₃. Чтобы изобразить работы А₆ и А₇, приходится ввести фиктивную работу, так как работе А₆ предшествуют три работы А₂, А₄ и А₅, а работе А₇ только работы А₂ и А₅. И наконец, дуга А₈, моделирующая выполнение заключительной работы А₈. Правильность нумерации событий можно проверить, воспользовавшись вышеизложенным алгоритмом.