Цена продажи изменяется в соответствии с кривой спроса
На конкурентном рынке увеличение объёма реализации сопровождается снижением цены продажи. Эта экономическая модель отличается от экономической модели при ограниченном спросе тем, что насыщения спроса удаётся преодолеть за счёт снижения цены. Максимальная цена продажи будет функцией от объёма реализации.
,
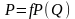(2.2.30)
Доход от реализации определяется как произведение цены на объём реализации
,
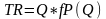(2.2.31)
Точка безубыточности определяется по формуле
,
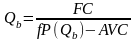(2.2.32)
Определение объём производства для достижения заданного объёма прибыли достигается по формуле
,
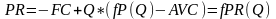(2.2.33)
Для определения максимальной и минимальной прибыли необходимо найти первую производную прибыли от Q и приравнять её к нулю.
,
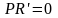(2.2.34)
Как можно заметить, данная модель не статична, все формулы зависят от функции цены от объёма реализации, определив которую можно установить все другие формулы модели. Поэтому перед использованием данной модели необходимо в обязательном порядке определить функцию цены от объёма реализации.
О
дним
из способов поиска этой функции является
корреляционно-регрессионный анализ.
Функция может иметь бесконечное
количество различных форм, однако,
исходя из теоретических соображений
(классическому виду кривой спроса) форма
зависимости должна быть обратной,
близкой к гиперболическому виду.
Рассмотрим пример.
Допустим, мы в ходе предварительного анализа определили, что:
,
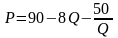(2.2.35)
Следовательно:
,
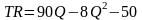(2.2.36)
,
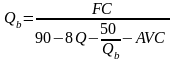(2.2.37)
,
(2.2.38)
Величина прибыли будет определяться по формуле:
,
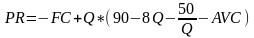(2.2.40)
,
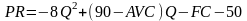(2.2.41)
Экстремумы данной функции прибыли определяются приравниванием первой производной к нулю.
,
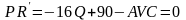(2.2.42)
,
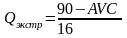(2.2.43)
Подставив полученное Q в формулу 2.2.41, мы получим величину максимальной прибыли от проекта:
,
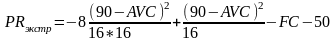(2.2.45)
,
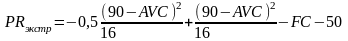(2.2.46)
,
(2.2.47)
,
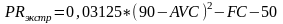(2.2.48)
Анализ чувствительности для бухгалтерской модели:
Изменение FC :
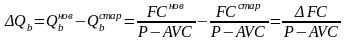
- Изменение AVC:
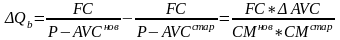
Изменение цены
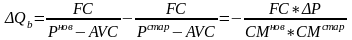
Практическая часть
Практическая часть лабораторной работы строится на персональном творческом выполнении задания – анализ безубыточности деятельности.
Исходные данные представляют собой 3 массива взаимоувязанных данных:
- количество произведенных и проданных изделий;
- себестоимость произведенных изделий;
- выручка от продажи однотипной продукции.
Проделанная работа должна помочь студенту определить следующие параметры по заданным массивам:
1) оценить взаимосвязи между количеством продукции и а) себестоимостью; б) выручкой; в) средней ценой продажи.
На данном этапе рассчитываются показатели корреляции и критерии Стьюдента для оценки их значимости.
Для проведения работы в Excel можно воспользоваться функцией =КОРРЕЛ(массив1;массив2) или (Сервис – Анализ данных – Регрессия)
Обязательно правильно построить графики зависимости.
2) определить параметры линейных уравнений взаимосвязи между количеством продукции и а) себестоимостью; б) выручкой.
Обязательно оцените близость полученного уравнения эмпирическим данным и укажите насколько существенна ошибка уравнения регрессии.
При решении задания исходите из бухгалтерской модели безубыточности со всеми допущениями.
Можно воспользоваться системой уравнений:
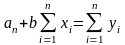
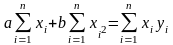
или его решением
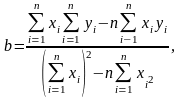
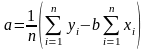
кроме того для определения параметра b можно воспользоваться функцией Excel =ЛИНЕЙН(массив1;массив2;ИСТИНА;ИСТИНА)
По итогам проведенного анализа выделите постоянную и переменную часть расходов, точку безубыточности, уравнение прибыли и все возможные параметры или элементы маржинального анализа.
Определите, как повлияет на величину точки безубыточности: а) рост постоянных расходов на 1%; б) рост переменных расходов на 1%; в) снижение цены на 1%.
Если Вы чувствуете в себе силы и готовы существенно усложнить исследование, дополните результаты следующим этапом (задание на «отлично»)
3) Предположим, что выручка и себестоимость изменяются не линейно, а параболически, т.е. цена не постоянна и снижается по мере насыщения рынка при этом общая величина расходов растет не прямолинейно и увеличивается по мере истощения рынка ресурсов.
Определите параметры параболических уравнений взаимосвязи между количеством продукции и а) себестоимостью; б) выручкой; в) валовой прибылью (разница между выручкой и себестоимостью).
Обязательно оцените близость полученного уравнения эмпирическим данным и укажите насколько существенна ошибка уравнения регрессии. Постройте необходимые графики.
При расчетах воспользуйтесь следующей системой уравнений:
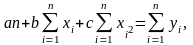
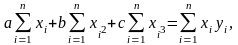
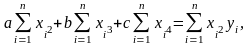
Определите объемы выпуска, при которых выручка и прибыль будут максимальными, а также точку (точки) безубыточности.
Для определения данных параметров воспользуйтесь формулами из курса базовой математики, а именно:
- вершина параболы (точка, в которой функция достигает своего экстремума – минимума или максимума) – т.н. точка А с параметрами
где дискриминант
- точки, в которых функция равна 0 – решения квадратного уравнения
Необходимо помнить:
если D>0, таких решений будет 2;
если D=0, решение будет одно х= -b/2a
если D<0, решений не будет вовсе.
Результат оформить в виде аналитической записки.
Поскольку корреляционный и регрессионный анализ выполнялся на различных дисциплинах неоднократно, то шаблон решения, его последовательность или графическое выполнение должны быть разработаны на занятии студентами самостоятельно. При выполнении работы следует учесть такие рекомендации:
Максимально автоматизируйте и оптимизируйте процесс. В данном случае Вы не обучаетесь, а отражаете качество накопленных ранее знаний и полученных умений
Сведите потребность в последующей работе аналитика с моделью к минимуму, т.е. при изменении данных основные параметры, графики и уравнения должны пересчитываться автоматически.
Правильно и качественно оформите результаты работы: даже человеку далекому от анализа должны быть понятны основные выводы, сделанные аналитиком.
Если необходимо, по ходу расчета делайте краткие пояснения, чтобы в итоге было проще разобраться в полученных данных.
Представьте разнообразную информацию об объекте исследования, даже если данное исследование в задании не значится.