5.3 Численное дифференцирование на основе интерполяционной формулы Ньютона.

Запишем для функции , заданной своими значениями в равноотстоящих узлах первый интерполяционный многочлен Ньютона

(5.15)

Продифференцировав, получим:

(5.16)

Подобным путем можно получить и производные функции более высоких порядков. Однако каждый раз, вычисляя значение производной функции в фиксированной точке , в качестве следует брать ближайшее слева узловое значение аргумента.

i	xi	yi	у	2у	3у	4y	5y
0	1,5	1,844535
			0,245461
1	1,6	2,089996		0,023915
			0,269376		-0,000450
2	1,7	2,359372		0,023465		0,000077
			0,292841		-0,000373		-0,000022
3	1,8	2,652213		0,023092		0,000055
			0,315933		-0,000318
4	1,9	2,968146		0,022774
			0,338707
5	2,0	3,306853

Таблица 5.2

Особенно просто формула (5.16) выглядит для одного из узлов. Так как в этом случае каждый узел можно считать начальным, при имеем:

(5.17)

Пример 5.4 Пусть . Выполним интерполирова­ние на отрезке [1,5;2,0] с шагом 0,1.

Составим таблицу конечных разностей (табл. 5.2). Вычислим по формуле (5.17)

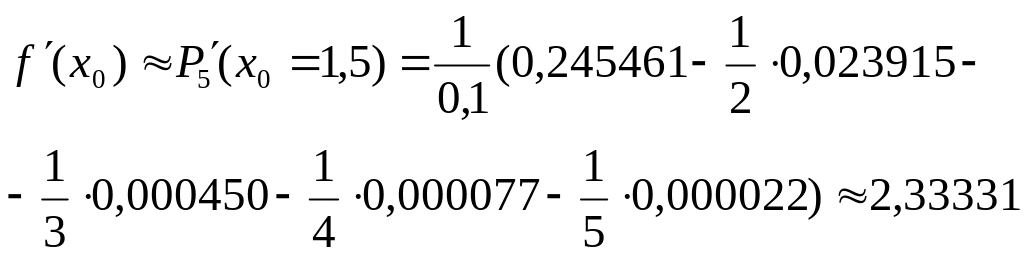
Для сравнения продифференцируем функцию, лежащую в ос­нове табл. 5.2, аналитически и найдем ее значение в той же точ­ке: при , т.е. имеет место высокая степень совпадения “точного” значения с найденным путем дифференцирования интерполяционного многочлена.

В то же время задача численного дифференцирования в такой постановке некорректна, из чего следует, что в общем случае нет оснований ожидать таких хороших результатов.

Для вывода формулы погрешности дифференцирования вос­пользуемся, применительно к первому интерполяционному многочлену Ньютона, формулой (5.11) и запишем:

где — некоторое промежуточное значение между узлами и заданной точкой .

Предполагая, что дифференцируема раз, получим для оценки погрешности дифференцирования (по аналогии с формулой (5.12)):

(5.18)

Для случая оценки погрешности в узле таблицы (когда и ) будем иметь удобный вид формулы (5.18):

(5.19)

Здесь учтено, что при ,

Пример 5.5 Оценим погрешность численного дифференцирова­ния, связанную с примером 5.4 Применяя формулу (5.19), при имеем: Таким об­разом, что вполне согласуется с реальной погрешностью, оцененной выше.

Таким образом, для корректного использования численного дифференцирования с помощью классических интерполяционных многочленов (Лагранжа и Ньютона) следует точку, в которой ищется производная, сделать узлом интерполяции.

Однако здесь явно присутствует логическое противоречие: если функция задана аналитически (пусть даже и достаточно слож­ным образом), аналитическое дифференцирование обычно вы­полнить существенно проще, чем описанную выше численную процедуру.

Если же функция исходно задана таблично, то становится про­блематичной оценка погрешности численного дифференцирова­ния по формуле (5.18), поскольку эта формула включает значе­ние производной старшего порядка, найти которое при отсут­ствии аналитической формулы, строго говоря, невозможно. Прак­тический выход из этого обстоятельства таков: следует воспользо­ваться аналогией между производными и конечно-разностными отношениями: и принять в качестве оценки погрешности, альтернативной (5.19), оценку:

(5.20)

Применительно к примеру 5.4 эта оценка дает: что всего вдвое превышает более корректную оценку, сделанную в примере 5.5.

Особо отметим простейшую аппроксимацию производных, основанную на линейной интерполяции. Применительно к любому внутреннему узлу таблицы имеют место две очевидные аппрокси­мации — правосторонняя

(5.21)

и левосторонняя

(5.22)

Для крайнего левого узла возможна лишь аппроксимация (5.21), крайнего правого — (5.22). Комбинируя их, получим для случая равноотстоящих узлов (наиболее часто встречающегося в приложениях) симметричную центрально-разностную аппроксимацию

(5.23)

Действуя аналогично, можно построить аппроксимации старших производных. Например, для второй производной симметричная центрально-разностная аппроксимация получится в сле­дующем приближении: Теперь, если мы хотим ограничиться наименьшим возможным числом узлов в аппроксимационной формуле, следует для использовать левостороннюю аппроксимацию, а для — правостороннюю

(5.24)

Это трехузельная аппроксимация второй производной. Разумеется, она неприменима для крайних узлов, и для построения соответствующих формул надо брать иную аппроксимацию первой производной, например

(5.25)

и аналогично

(5.26)

Подобные формулы используются как для простейшего вычисле­ния значений производных в узлах заданной сетки, так и для других целей (в частности, в некоторых численных методах решения диф­ференциальных уравнений, рассматриваемых в следующей лабораторной работе).