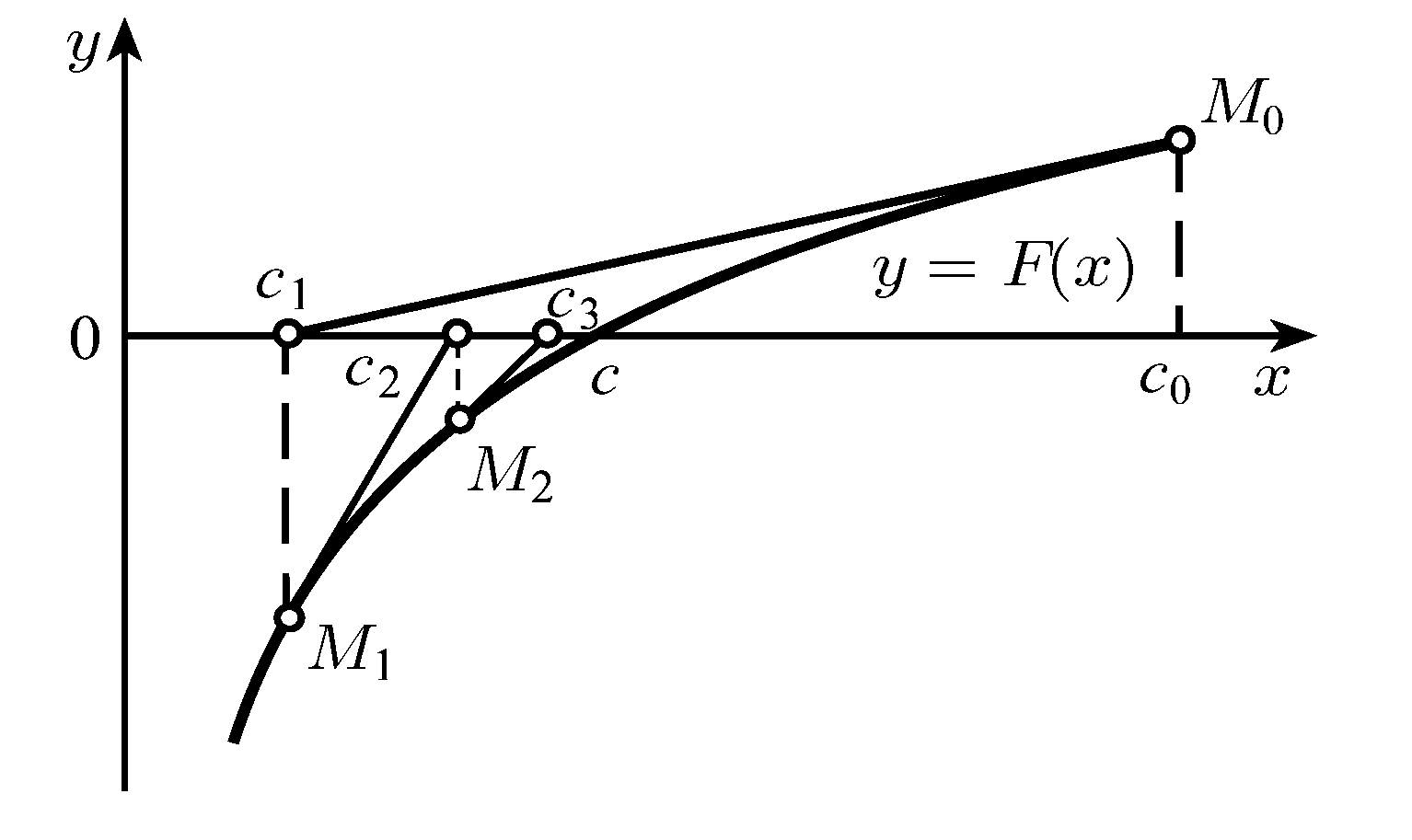
4. Метод Ньютона (метод касательных).

Его отличие от предыдущего метода состоит в том, что на к-й итерации вместо хорды проводится касательная к кривой у=F(x) при х=c_k-1 и ищется точка пересечения касательной с осью абсцисс. При этом не обязательно задавать отрезок [а, b], содержащий корень уравнения (2.1), а достаточно лишь найти некоторое начальное приближение корня х=с₀ (рис. 2.7). Уравнение касательной, проведенной к кривой у=F(x)в точке М₀ с координатами с₀ и F(c₀), имеет вид :

.

Отсюда найдем следующее приближение корня с₁ как абсциссу точки пересечения касательной с осью х (у=0):

Аналогично могут быть найдены и следующие приближения как точки пересечения с осью абсцисс касательных, проведенных в точках M₁, M₂ и т. д. Формула для к-го приближения имеет вид:

, к=1,2 и т.д. (2.7)

При этом необходимо, чтобы не равнялась нулю. Для окончания итерационного процесса могут быть использованы условия (2.5) или (2.6). Из (2.7) следует, что на каждой итерации объем вычислений в методе Ньютона больший, чем в рассмотренных ранее методах, поскольку приходится находить значение не только функции F(x), но и ее производной. Однако скорость сходимости здесь значительно выше, чем в других методах. Остановимся на некоторых вопросах, связанных со сходимостью метода Ньютона и его использованием. Имеет место следующая теорема.

Теорема. Пусть х=с — корень уравнения (2.1), т. е. F(c)=0, a F'(c) 0 и F"(x) непрерывна. Тогда существует окрестность D корня с (с D) такая, что если начальное приближение с_о принадлежит этой окрестности, то для метода Ньютона последовательность значений {c_k} сходится к с при к . При этом для погрешности корня имеет место соотношение:

Рисунок 2.7. Иллюстрация метода Ньютона.

Фактически это означает, что на каждой итерации погрешность возводится в квадрат, т. е. число верных знаков корня удваивается. Если ~1, то легко показать, что при | | 0,5 пяти-шести итераций достаточно для получения минимально возможной погрешности при вычислениях с двойной точностью. Действительно, погрешность теоретически станет в этом случае величиной порядка 2^-64, что намного меньше, чем максимальная погрешность округления при вычислениях с двойной точностью, равная 2^-53. Заметим, что для получения столь малой погрешности в методе половинного деления потребовалось бы более 50 итераций.

Пример 2.3. Для иллюстрации рассмотрим уравнение х²-0.25=0 и найдем методом Ньютона один из его корней, например х=с=0.5. Для данного уравнения F"(c)/2F'(c)=1. Выберем с₀=1, тогда =-0.5. Проводя вычисления с двойной точностью, получим следующие значения погрешностей:

.

Таким образом, после шести итераций погрешность в рамках арифметики с двойной точностью исчезла.

Трудность в применении метода Ньютона состоит в выборе начального приближения, которое должно находиться в окрестности D. При неудачном выборе начального приближения итерации могут расходиться.

Пример 2.4. Для уравнения arctgх=0 (корень х=с=0) при начальном приближении с_о=1.5 первые шесть итераций приводят к погрешностям

.

Очевидно, что итерации здесь расходятся. Для предотвращения расходимости иногда целесообразно использовать смешанный алгоритм. Он состоит в том, что сначала применяется всегда сходящийся метод (например, метод половинного деления), а после некоторого числа итераций — быстро сходящийся метод Ньютона.

Табличный процессор Ехсеl для решения уравнений располагает специальным средством Подбор параметра в меню Сервис. Его алгоритм скрыт от пользователя, но если важен именно результат, а не путь к нему, то обращение к стандартному средству оправданно. На рис. 2.8 показаны диалоговые окна Ехсеl при решении уравнения х²-sinх=0: левая часть уравнения записана в ячейке А1, начальное значение - в ячейке В1, результат - в ячейке В1.

Рисунок 2.8.Реализация средства Подбор параметра в Excel.