V підсумки уроку

1. Поясніть в якому випадку функцію F(х) називають первісною для функції f(x) на заданому проміжку. Наведіть приклади.

2. Метод «Ключові слова»

Зміст методу полягає у визначені «ключових» слів уроку, тобто основних термінів, які позначають знання які були отримані протягом уроку. Учні виділяють «ключові» слова уроку і пояснюють свою позицію.

Vі домашнє завдання

1. Конспект

2. Доведіть, що функція F(х) є первісною для функції f(x), якщо

1) , ,

2) , ,

3. Завдання на повторення. Знайдіть похідну функції:

1)

2)

Розв`язання домашнього завдання

2. Розв’язання.

1) За означенням первісної повинна виконуватися рівність:

. Це означає, що F(х) є первісною для функції f(x).

2) За означенням первісної повинна виконуватися рівність:

. Це означає, що F(х) є первісною для функції f(x).

3. Розв’язання.

1)

2)

Основна властивість первісної. Таблиця первісних

Мета: домогтися засвоєння основної властивості первісної, таблиці первісних, сформувати вміння знаходити первісні для функцій, користуючись таблицею первісних; розвивати спостережливість, уміння проводити логічні міркування; розвивати в учнів усну і письмову культуру мовлення, вчити користуватися словесною, символічною і графічною мовами математики; виховувати охайність при виконанні креслень і записів

Тип уроку: засвоєння знань, формування вмінь

Хід уроку

І ОРГАНІЗАЦІЙНИЙ МОМЕНТ

ІІ АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

Засвоєння матеріалу, що було вивчено на попередньому уроці, перевіряємо за допомогою гри «Вірю – не вірю»

1. Чи правильно, що якщо функція F(х) є первісною для функції f(x), то виконується рівність:

2. Чи правильно, що функція F(х) є первісною для функції f(x), якщо:

1. ,

2. ,

3. ,

4. ,

5. ,

6. ,

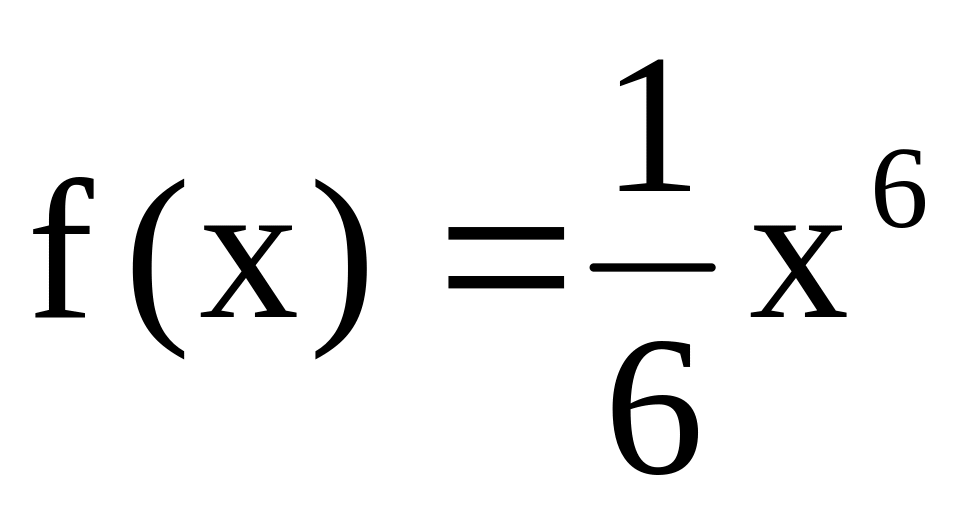
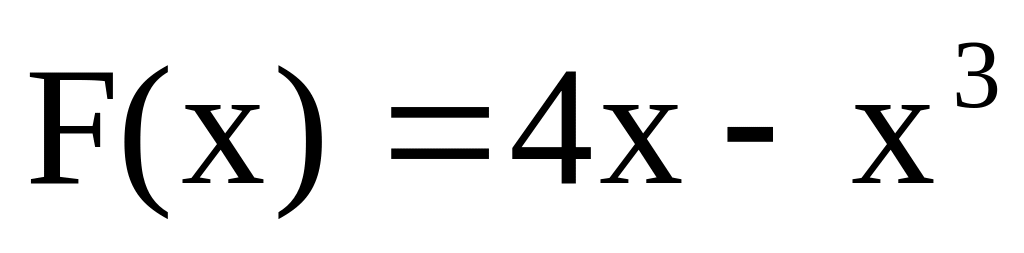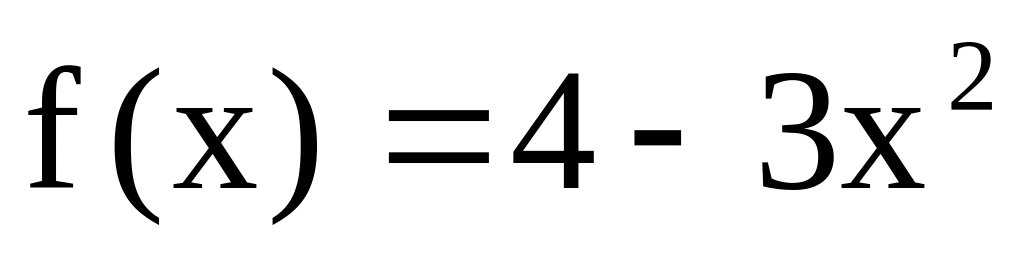
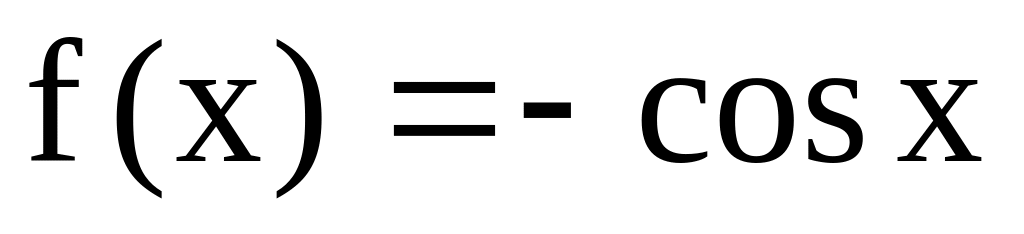
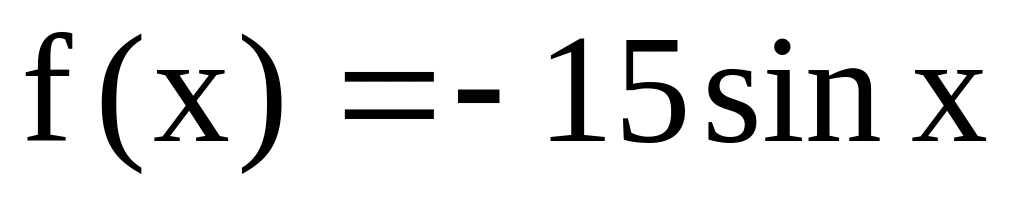
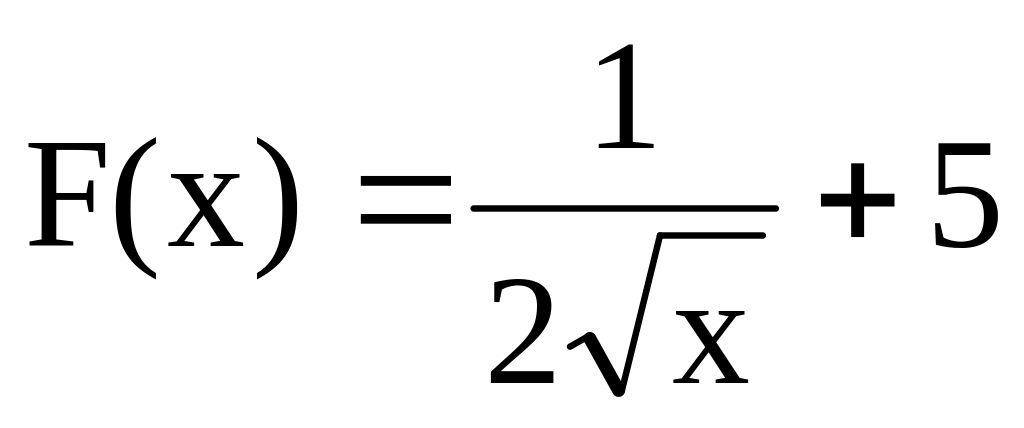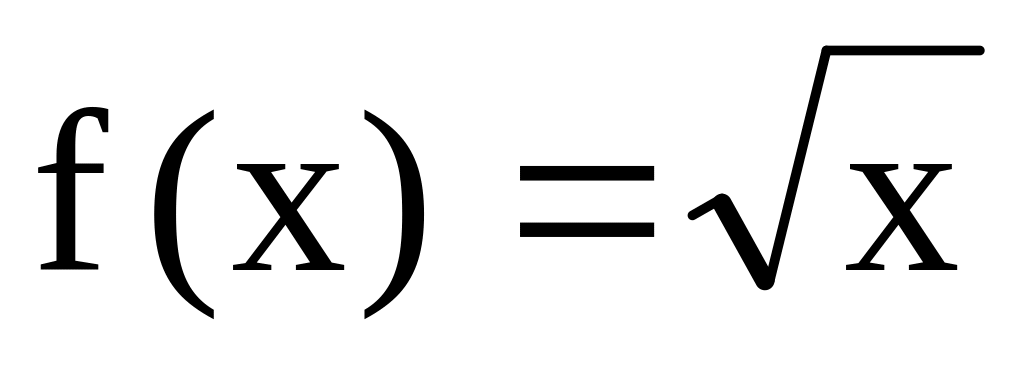
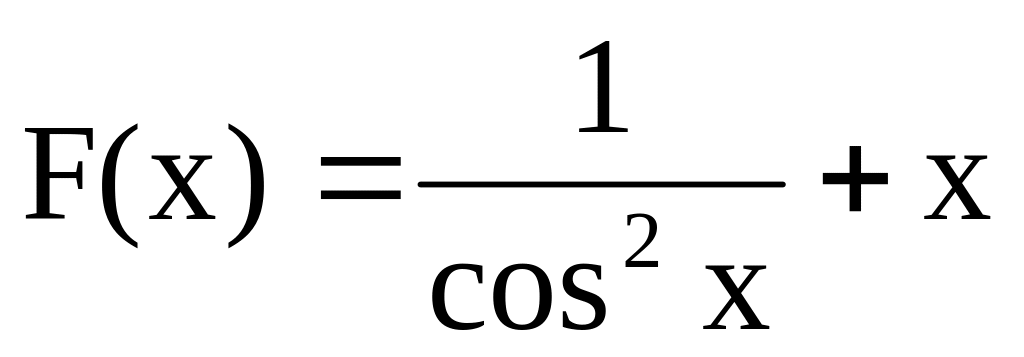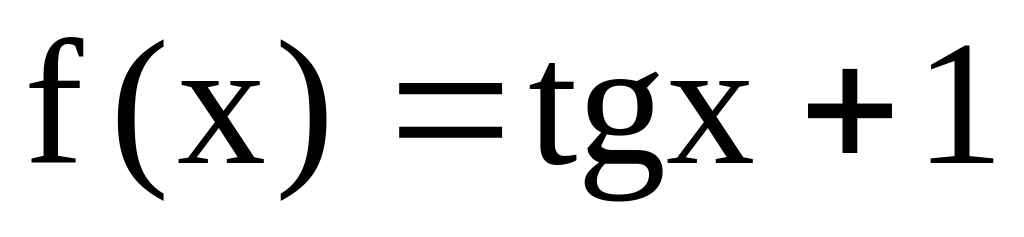
Відповідь: так; ні; так; ні; так; ні; ні.

ІІІ СПРИЙМАННЯ І УСВІДОМЛЕННЯ НОВОЇ ТЕМИ

Розглянемо функцію . Доведемо, що функції , , є первісними функції f(x).

Взагалі, будь-яка функція , де С – постійна, є первісною функції . Це випливає з того, що похідна постійної дорівнює нулю.

Цей приклад свідчить, що для заданої функції первісна визначається неоднозначно.

Якщо функція F(х) є первісною для функції f(x) на поданому проміжку, а С – довільна стала, то функція F(х)+С також є первісною для функції f(x), при цьому будь-яка первісна для функції f(x) на поданому проміжку може бути записана у вигляді F(х)+С, де С – довільна стала.

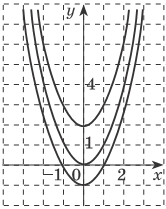
Основній властивості первісної можна надати геометричного змісту: графіки будь-яких двох первісних для функції f(x) одержуються один із одного паралельним перенесенням вздовж осі ОY

Нехай функція f(x) має на деякому проміжку первісну. Сукупність всіх первісних для функції f(x) на проміжку називають невизначеним інтегралом цієї функції і позначають . Функцію f(x) називають підінтегральною функцією.

З основної властивості первісних випливає, що , де F(х) – яка-небудь первісна для функції f(x) на даному проміжку, С – довільна стала (її називають сталою інтегрування). Наприклад, функція є первісною для функції на проміжку (-∞;+∞), тому можна записати, що .

Для функцій, похідні яких відомі, складена таблиця первісних (таблиця невизначених інтегралів)

ІV ПЕРВИНЕ ЗАКРІПЛЕННЯ І КОРЕКЦІЯ

1. Обчисліть: 1) одну з первісних для функції на множині всіх дійсних чисел; 2) усі первісні для функції ; 3)

Розв’язання:

1. Однією з первісних для функції на множині дійсних чисел є 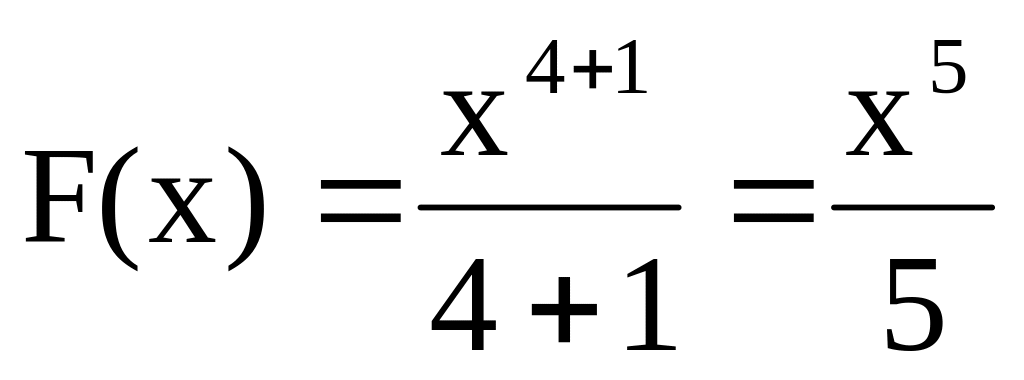, оскільки

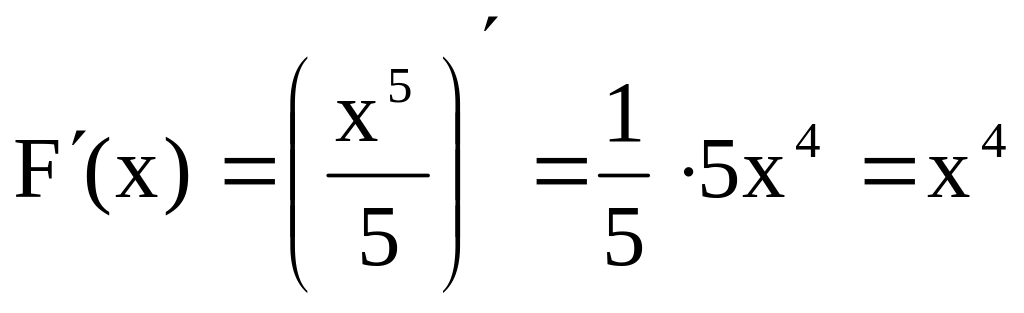
2. За основною властивістю первісних усі первісні для функції можна записати у вигляді 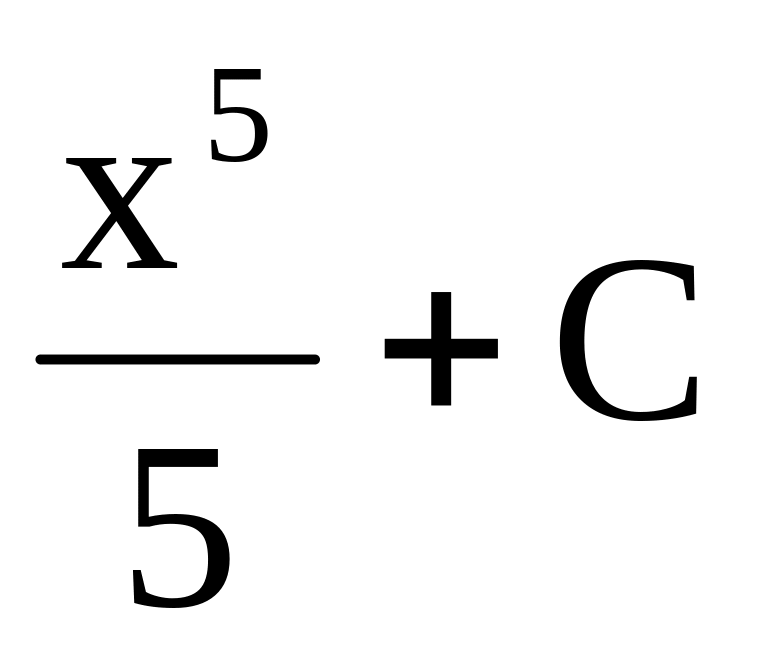, де С – довільна стала

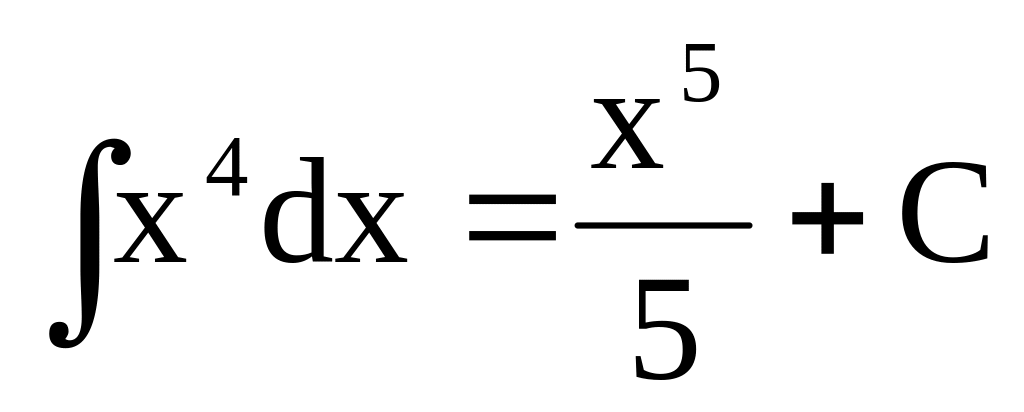3. , де С – довільна стала

2. Знайдіть загальний вигляд первісних для функцій (первісна знаходиться на проміжку, що входить до області визначення функції), запишіть за допомогою невизначеного інтегралу.

1)

Розв’язання:

, оскільки

2)

3)

4)

5)

Розв’язання:

, оскільки

6)

7)

8)

9)

10)

11)

12)

13)

14)

Розв’язання:

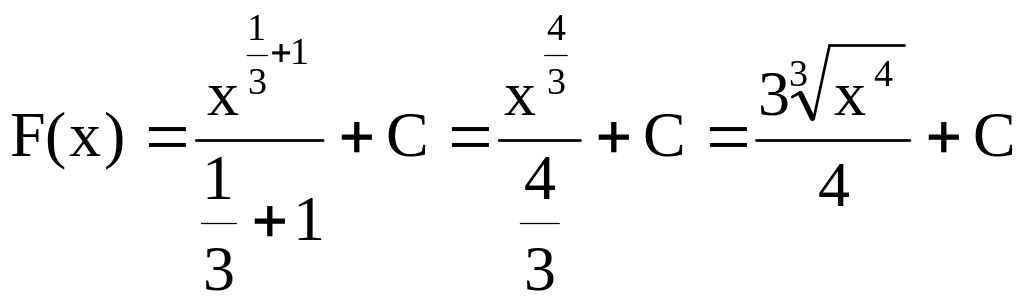, оскільки

15)

Розв’язання:

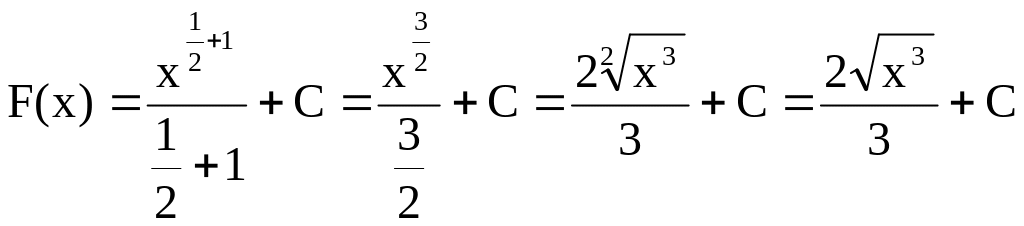, оскільки