Лабораторна робота №1 статистична обробка результатів вимірювань

Мета роботи: опанувати методику статистичної обробки результатів експериментальних досліджень.

2.1 Загальні відомості

До випадкового розсіювання результатів вимірювання призводять різні неконтрольовані фактори врахування дії яких буває неможливим. Зменшення їх впливу здійснюють за допомогою багаторазових вимірювань з застосуванням відповідного статистичного опрацювання яке пов'язане з використанням характеристик випадкових величин.

Випадковою називають величину, яка непередбачувано змінюється і її подальші значення на основі попередніх досліджень можна прогнозувати лише з певною ймовірністю.

Можна виділити дві ідеалізовані задачі, у яких спостерігається випадкова величина. Перша задача стосується регулярних, зокрема майже сталих, вимірюваних величин, спотворених випадковими у часі впливами. Її послідовні значення змінюються у часі хаотично відносно певного значення.

Інша задача стосується величин, які самі по собі мають випадкові значення, наприклад, вага (маса). Тоді існують випадкові значення у просторі набору значень. Під час графічного подання таких випадкових величин аргументом є номер елемента у серії вимірювань.

Незважаючи на хаотичність часових змін випадкових величин, протягом довшого інтервалу часу можна спостерігати певні закономірності їхніх змін. Зокрема, послідовні значення випадкової величини можуть групуватися навколо певного значення, яке може бути сталим чи мати тенденцію до регулярної зміни, а інтервал розкиду значень випадкової величини може також мати тенденцію до певної стабілізації. Аналогічно і випадкові величини також характеризуються певними стабільними параметрами, зокрема, певним стабільним середнім значенням з певним, стабільним розкидом навколо середнього значення. Для дослідження властивостей випадкової величини широко використовують її незалежні послідовні результати спостережень, які записують у вигляді послідовного ряду:

х_х, х₂,...х_п. (2.1)

Отриманий ряд прийнято називати вибіркою х_(n) членами якого є отримані результати х_і, а кількість результатів п називають розміром вибірки. Очевидно, що експериментатор завжди має справу зі скінченою за розміром вибіркою, тобто з кількістю спостережень При цьому для тієї самої випадкової величини можна отримати довільну кількість різних вибірок як однакового так і різного розміру.

Експериментальну вибірку характеризують параметрами, які насамперед вказують на центр групування (положення) елементів вибірки (результатів спостережень) на числовій осі, а також на ступінь їхнього розпорошення (розсіювання) навколо цього центру. Зокрема, часто положення вибірки на числовій осі характеризують середніми значеннями: середнім арифметичним, середнім геометричним, середнім гармонічним значеннями вибірки, а також іншими параметрами, такими як центром розмаху, медіаною, модою тощо. Розпорошення вибірки характеризують так званим розмахом (чи його половиною), вибірковою дисперсією, коефіцієнтом асиметрії значень вибірки тощо. У математичній статистиці такого типу параметри називають точковими, оскільки вони виражаються одним числом, вказують на певну точку (місце) в експериментальному розподілі та належать до широкої гами вибіркових характеристик.

Середнє (арифметичне) значення вибірки:

(2.2)

є однією із характеристик центру, навколо якої групуються можливі значення випадкової величини.

Очевидно, що середнє значення є також випадковою величиною, оскільки, взявши іншу вибірку навіть такого самого розміру, яка буде відрізнятися від попередньої хоча би в одному члені, отримаємо дещо інше середнє значення. Середні значення фізичних величин відрізняються між собою значно менше ніж значення цих величин у вибірках.

При необмеженому збільшенню обсягу вибірки "випадковість" (розкид) середнього значення зменшується, тобто воно стає щораз стабільнішим і у своїй границі переходить у так зване математичне сподівання випадкової величини т_х:

. (2.3)

Математичне сподівання є невипадковою, теоретичною характеристикою випадкової величини, а на практиці стикаються лише із його наближенням (оцінкою) – середнім значенням.

Залежність (2.3) записують у вигляді

, (2.4)

де М – символ знаходження математичного сподівання, що означає математичне сподівання середнього значення є математичним сподіванням самої випадкової величини.

Генеральна сукупність. За необмеженого зростання обсягу вибірки вона переходить у генеральну сукупність – тобто вибірку, яка охоплює всі можливі значення. Кожну практичну вибірку меншого обсягу ніж генеральна сукупність розглядають як вибірку із генеральної сукупності. Отже математичне сподівання – це середнє значення генеральної сукупності, а середнє значення практичних вибірок можуть відрізнятись між собою і тим більше, чим менший їх обсяг.

Вибіркова дисперсія. Мірою розкиду, розсіювання (чи випадковості або нестабільності), експериментальної вибірки відносно середнього значення, є випадкова дисперсія – (випадкова варіація), яку визначають як середнє значення квадратів відхилень елементів вибірки від їхнього середнього значення:

. (2.5)

У разі необмеженого зростання кількості спостережень (загалом при тобто переході до генеральної сукупності, вибіркова дисперсія переходить у свою теоретичну характеристику - дисперсію випадкової величини:

. (2.6)

Отже, вибіркова дисперсія є конкретним наближенням (оцінкою) дисперсії випадкової величини.

Аналогічно до виразу (2.4), залежність (2.6) записують у вигляді

, (2.7)

що означає, що математичне сподівання вибіркової дисперсії є дисперсією самої випадкової величини.

Як було зазначено вище, вибіркова дисперсія (як і сама дисперсія) має розмірність квадрата випадкової величини. Квадратний корінь з вибіркової дисперсії називається вибірковим стандартним відхиленням результатів спостережень:

, (2.8)

яке є випадковою величиною, тобто для різних вибірок однакового чи різного обсягу (розміру) має дещо різні значення, які зі збільшенням обсягу вибірки стабілізуються.

За необмеженого зростання кількості спостережень (тобто з наближенням до генеральної сукупності) вибіркове стандартне відхилення переходить у свою теоретичну характеристику - стандартне відхилення:

. (2.9)

Стандартне відхилення має розмірність випадкової величини.

Очевидно, що як і для кожної окремої вибірки мірою розкиду середніх значень є вибіркова дисперсія середнього значення. Для її експериментального оцінювання необхідно мати не одну, а достатньо велику кількість k вибірок з обсягом п результатів спостережень.

Отримавши k вибірок, послідовно знаходять: вибіркові середні значення кожної вибірки за формулою (2.2). Потім розраховують вибіркове середнє значення із середніх значень вибірок, а далі використовуючи ці значення за виразом, подібним до (2.5), знаходять вибіркову дисперсію середніх значень вибірок:

. (2.10)

Вибіркове стандартне відхилення середніх значень вибірок знаходять за виразом, подібним до виразу (2.8):

. (2.11)

Якщо кількість вибірок k заданого обсягу п теоретично збільшувати так, що утвориться генеральна сукупність вибірок розміром п, то загальне вибіркове середнє значення середніх значень окремих вибірок прямує до математичного сподівання (теоретичного значення), а вибіркова дисперсія середніх значень (2.10) вибірок обсягом п прямує до дисперсії середніх значень, яка у п разів менша за дисперсію самої вибірки:

. (2.12)

Аналогічно стандартне відхилення (міра нестабільності чи розсіювання) середнього значення вибірок обсягом п у разів менше за стандартне відхилення самої вибірки:

. (2.13)

Вибіркові оцінки дисперсії та стандартного відхилення середнього значення вибірки обсягом п із незалежними результатами спостережень можна знайти за виразами

, . (2.14)

Як видно з цих формул можливе розсіювання ("випадковість") середніх значень вибірки відносно розсіювання ("випадковості") окремих результатів спостережень (членів вибірки) зменшується пропорційно до квадратного кореня із обсягу вибірки. Тобто, якщо хочемо зменшити розсіювання можливих середніх значень у п=10 разів, обсяг вибірки потрібно збільшити у п=10²=100. Для зменшення розкиду можливих середніх значень ще у 10 разів (загалом у 100 разів) кількість спостережень повинна становити n=100²=10000 результатів. Отже, стабільність середніх значень вибірки із збільшенням її обсягу спочатку швидко покращується, але надалі це покращання вже не таке відчутне.

Медіана - це також характеристика центру групування значень випадкової величини, яку знаходять як значення серединного елементу впорядкованої вибірки. Впорядкована вибірка – це вибірка, просортована за зростанням чи спаданням, яку ще називають варіаційним рядом:

xс₁ < хс₂ < хс₃ < ... < хс_п. (2.15)

Якщо кількість спостережень непарна, то за медіану приймають центральний елемент (з середнім номером) впорядкованої вибірки:

, (2.16)

якщо ж кількість спостережень парна, то медіана – середнє значення з двох центральних елементів впорядкованої вибірки:

. (2.17)

Серед багатьох інших статистичних характеристик випадкової вибірки медіана є однією з найстійкіших до впливу аномальних результатів. Крім того, медіану простіше знайти ніж середнє значення.

Розмах вибірки - це різниця між найбільшим та найменшим значеннями впорядкованої вибірки:

V = хс_п- хс₁. (2.18)

Розмах вибірки є також мірою розсіювання значень вибірки, яку дуже легко (порівняно із вибірковими дисперсією чи стандартним відхиленням) обчислити, однак у багатьох випадках розмах є дуже чутливим до аномальних результатів, тобто нестабільним. Для опису випадкової величини часто використовують піврозмах вибірки як половину розмаху:

. (2.19)

Центр (середина) розмаху вибірки – це ще одна міра центру групування можливих значень вибірки, яку знаходять як середнє значення із найбільшого та найменшого значень впорядкованої вибірки:

. (2.20)

Хоча середина розмаху, як середнє значення та медіана, характеризує центр групування можливих значень вибірки, але як сам розмах, так і його середина є дуже чутливими до можливих аномальних результатів (викидів, промахів).

На рис. 2.1 показано медіану, розмах, піврозмах та центр розмаху вибірки, які характеризують групу студентів.

Рисунок 2.1 ‑ Медіана, розмах, піврозмах та центр розмаху росту групи студентів

Приклад 2.1. Обстежили групу з 25-ти студентів і отримали такі значення їхнього росту h_і з точністю до половини сантиметра:

179,5 170,0 174.5 171,5 179,5 173,5 163,0 175,5 181,0 169,5 175,5 167,5 173,5 172,5 177,5 170,0 170,5 175,5 173,0 173,0 172,5 176,0 166,5 175,0 171,0.

Показники росту студентів цієї групи утворюють випадкову вибірку розміром п = 25.

Для наведеної вибірки росту студентів знайти її медіану та характеристики розмаху.

Розв'язання. Спочатку просортуємо вибірку росту студентів у групі (вишикуємо їх за ростом):

163,0 166,5 167,5 169,5 170,0 170,0 170,5 171,0 171,5 172,5 172,5 173,0 173,0 173,5 173,5 174,5 175,0 175,5 175,5 175,5 176,0 177,5 179,5 179,5 181,0;

Медіана вибірки росту студентів у групі. Оскільки чисельність студентів у групі (вибірці) становить п = 25, (кількість студентів непарна -25) то медіана росту студентів даної групи дорівнює росту студента із серединним 13 номером у строю, вишикуваним за зростанням см. Показник росту студентів у наведеному вище впорядкованому списку, за яким визначено медіану, показано жирним шрифтом.

Розмах. Розмах знаходять як різницю росту найвищого та найнижчого студентів (у впорядкованому списку показники росту цих студентів підкреслено). Тому VI = hс₂₅–hс₁, = 181,0 – 163,0 = 18,0 см;

Піврозмах. Він дорівнює половині розмаху, тобто

R = V/2 = 18/2 = 9,0 см;

Центри розмахів. Центр розмаху знаходять як середнє значення росту найвищого та найнижчого студентів.

Тому х_с=(hс₂₅ +hс₁)/2=172,0 см.

Зазначимо, що внаслідок стійкості медіани вибірки, її, поряд із середнім значенням, можна застосовувати як серединну оцінку вибірки.

Числові характеристики (середнє значення, вибіркові дисперсія та стандартне відхилення, тощо – їх ще називають точковими) не повністю характеризують випадкову величину, зокрема з погляду частості появи тих чи інших значень величини. Однією з найповніших характеристик випадкової величини є густина (щільність) розподілу її значень р(х). Власне вона характеризує частість появи тих чи інших значень цієї величини.

Залежно від того, яких значень може набувати випадкова величина, густина розподілу може бути дискретною з квантованими значеннями випадкової величини або неперервною функцією.

Оскільки результати вимірювань завжди подаються скінченною кількістю цифр, то всі експериментально знайдені розподіли величин є дискретними. Неперервну густину розподілу величини можна трактувати як теоретичну модель, чи граничний перехід дискретного розподілу у неперервний за зменшення кроку квантування до нуля, що також, строго кажучи, є теоретичною конструкцією.

Отже, загалом за скінченного обсягу експериментальної вибірки та ненульового кроку її квантування розподіл (який в цьому випадку теж є експериментальним) випадкової величини є дискретним. Відношення кількості п_р випадань результату х_ср із просортованої послідовності до загальної кількості спостережень п називають відносною частотою результату:

, (2.21)

а сукупність відносних частот (2.21) – статистичним розподілом вибірки. Його називають емпіричним (експериментальним), оскільки частоти появи окремих результатів знайдені за експериментальними (емпіричними) даними. Для побудови емпіричного розподілу використовують впорядковану послідовність результатів спостережень – варіаційний ряд (2.15).

Відносна частота результату є оцінкою ймовірності р_р появи такого значення величини, яка є граничним значенням відносної частоти, якщо кількість спостережень прямує до нескінченності:

. (2.22)

У кожному конкретному випадку різні величини можуть мати різний розподіл. Для зручності аналізу використовують теоретичні моделі розподілів, яких також є величезне розмаїття. Зручність використання теоретичних моделей розподілу полягає у тому, що для них заздалегідь відомі вирази для розрахунку їх числових характеристик (наприклад, математичного сподівання, дисперсії, стандартного відхилення тощо) і, крім того, ці вирази, як правило, залежать від невеликої кількості параметрів розподілу - переважно 2—3-х. Тому, знаючи ці параметри, підстановкою їх у відповідні вирази відразу (оминаючи підсумовування чи інтегрування та інші математичні операції) можна визначити значення потрібних характеристик.

На практиці використовують вироджений (причинний) розподіл, рівномірний розподіл, нормальний розподіл і ін.

При порівняно невеликому обсягу вибірок на основі статистичного розподілу досить важко встановити вигляд розподілу випадкової величини. Для цього потрібно мати вибірку в кілька сотень (а часто навіть і тисяч) результатів спостережень. А це, в свою чергу, вимагає значних експериментальних затрат.

Певним вирішенням такої проблеми є усереднення отриманого статистичного розподілу у формі гістограми та полігона, які є певними аналогами густини розподілу випадкової величини. Операція усереднення полягає у тому, що гістограму і полігон будують не для кожного можливого результату спостереження, як це роблять для статистичного розподілу, а для груп результатів, які потрапляють у деякий інтервал певної ширини h.

Гістограмою називають ступеневу фігуру, утворену з прямокутників сталої ширини Н, висоти яких дорівнюють частотам потрапляння результатів у відповідні інтервали, а полігоном, називають ламану, відрізки якої сполучають точки, що відповідають серединам верхніх основ прямокутників гістограми (рис. 2.2, а і б відповідно).

а)	б)
Рисунок 2.2 ‑ Гістограма (а) та полігон (б)

Для побудови гістограми спочатку знаходять розмах вибірки за формулою (2.18).

Потім його ділять на r інтервалів шириною

(2.23)

У чисельнику (2.23) введено доданок, що дорівнює одиниці молодшого розряду (ОМР), з урахуванням того, що у інтервалі х_сп — х_с1 завжди міститься на одне числове значення більше ніж кількість квантів. Наприклад, для двох квантів (ОМР) є три результати: х₁ , х₂=х₁+ОМР, x₃ = x₁+20МР тощо.

Якщо кількість результатів спостережень невелика (кілька десятків), можна використати залежність

. (2.24)

Для значніших за обсягом вибірок (сотні, тисячі і більше) існують інші залежності. Як правило рекомендована кількість інтервалів досить невелика і знаходиться в межах від ~7 до ~22.

Для знайденої ширини границі сусідніх інтервалів становлять

. (2.25)

Причому ліва границя входить до цього інтервалу, а права - до наступного, тобто до j-го інтервалу потрапляють результати спостережень, які задовольняють умову

. (2.26)

Підрахувавши кількість результатів n_j які потрапили до кожного j-го інтервалу, можна визначити емпіричну частоту потрапляння у цей інтервал за виразом

. (2.27)

Отримані за (2.27) значення відповідають висотам відповідних прямокутників гістограми (рис. 2.2).

Приклад 2.2

Таблиця 2.1 Задані вибірки

1с	1,210	1,228	1,230	1,231	1,231	1,232	1,233	1,238
1,240	1,241	1,242	1,242	1,242	1,243	1,243	1,244	1,245
1,248	1,248	1,249	1,249	1,249	1,249	1,250	1,250	1,250
1,253	1,255	1,255	1,255	1,255	1,257	1,257	1,258	1,260
1,261	1,261	1,263	1,264	1,264	1,265	1,267	1,270	1,274
1,274	1,276	1,276	1,282	1,289	1,293
2с:	1,209	1,217	1,220	1,228	1,229	1,230	1,230	1,231
1,232	1,234	1,234	1,235	1,236	1,237	1,237	1,239	1,240
1,240	1,242	1,243	1,243	1,246	1,247	1,248	1,248	1,248
1,249	1,250	1,250	1,250	1,252	1,252	1,252	1,253	1,253
1,254	1,256	1,257	1,257	1,258	1,258	1,258	1,258	1,259
1,262	1,263	1,272	1,273	1,277	1,285.
3с:	1,202	1,209	1,219	1,226	1,227	1,228	1,231	1,231
1,232	1,235	1,235	1,235	1,237	1,239	1,240	1,241	1,242
1,242	1,242	1,242	1,243	1,243	1,243	1,244	1,245	1,249
1,250	1,251	1,251	1,252	1,254	1,255	1,256	1,256	1,258
1,260	1,264	1,264	1,268	1,269	1,272	1,272	1,274	1,275
1,275	1,277	1,277	1,278	1,279	1,285.
4с:	1,217	1,222	1,222	1,228	1,229	1,230	1,230	1,234
1,234	1,236	1,237	1,238	1,240	1,240	1,240	1,240	1,241
1,241	1,244	1,244	1,246	1,246	1,249	1,250	1,251	1,252
1,256	1,256	1,257	1,257	1,257	1,258	1,259	1,259	1,261
1,261	1,262	1,262	1,264	1,265	1,266	1,266	1,266	1,269
1,271	1,278	1,279	1,281	1,282	1,287.
5с:	1,207	1,210	1,216	1,224	1,231	1,233	1,234	1,235
1,237	1,237	1,241	1,245	1,245	1,245	1,249	1,249	1,249
1,250	1,250	1,250	1,251	1,251	1,251	1,252	1,252	1,253
1,254	1,255	1,255	1,255	1,256	1,256	1,256	1,257	1,258
1,258	1,259	1,260	1,260	1,260	1,262	1,263	1,266	1,267
1,268	1,268	1,271	1,273	1,274	1,297.

Для заданої вибірки 1_с побудувати гістограму.

Розв'язання. Оскільки обсяг вибірки невеликий, п=50, кількість інтервалів знайдемо за (2.24) . Зауважимо, що кількість інтервалів за формулою Старджеса

, (2.28)

становить r= 1+3,3lg50= 6,6 = 7, тобто отримуємо таке саме значення.

Оскільки розмах вибірки V = 1,293-1,210 = 0,083 мВ, то ширина інтервалів групування результатів (2.23):

h =(0,083 + 0,001)/7 = 0,012 мВ.

Для заданих результатів ці границі інтервалів групування становлять:

1,210; 1,222; 1,234; 1,246; 1,258; 1,270; 1,282; 1,294.

Порівнюючи просортовані результати для першої вибірки (1_с) із отриманими границями інтервалів, знаходимо такі кількості потраплянь результатів до відповідних інтервалів:

: 1; 6; 10; 16; 9; 5; 3.

Відповідні емпіричні частоти розраховані за формулою (2.27) становлять : 0,02; 0,12; 0,20; 0,32; 0,18; 0,10; 0,06.

На рис. 2.3, а показано гістограму, яку побудовано на основі одержаних значень.

Очевидно, що сума емпіричних частот повинна становити 1. Загалом на осі абсцис гістограми необхідно відкладати відповідні значення границь інтервалів поділу значень результатів спостережень. Однак для спрощення на рис.3.3, а показано лише номери цих інтервалів, а абсолютні значення їхніх границь можна знайти за (2.25).

Також існує інша методика побудови гістограми, у якій висота прямокутників дорівнює не емпіричній частоті , а просто кількості потраплянь результатів у встановлені інтервали. Очевидно, що у такому разі форма гістограми не зміниться (зміниться лише вертикальний масштаб), а сума висот прямокутників дорівнює обсягу вибірки.

Рисунок 2.3 ‑ Гістограма наведених у прикладі 2.3 п’яти вибірок

Приклад 2.3 Побудувати гістограми решти чотирьох вибірок, просортовані значення яких наведено у прикладі 2.2 табл. 2.1.

Розв'язання. Оскільки обсяги вибірок такі самі, як у першої вибірки, то, скориставшись методикою, наведеною у прикладі 2.2, знайдемо кількості потраплянь ( ) у встановлені 7 інтервалів

Таблиця 2.2

п2j	2	5	11	15	13	2	2;
пЗj	2	1	10	13	10	6	8;
п4j	3	8	11	9	12	2	5;
п5j	3	2	9	22	11	2	1

Перевіркою встановлюємо, що сума потраплянь у всі сім інтервалів дорівнює обсягу вибірки, тобто 50.

Таблиця 2.3

w2j	0,04 0,10	0,22	0,3	0,26	0,04	0,04;
w3j	0,04 0,02	0,20	0,26	0,20	0,12	0,16;
w4j	0,06 0,16	0,22	0,18	0,24	0,04	0,10;
w5j	0,06 0,04	0,18	0,44	0,22	0,04	0,02.

Перевіркою встановлюємо, що сума емпіричних частот для кожної з вибірок дорівнює одиниці;

Відповідні гістограми показано на рис. 2.3, б, в, г, д.

Зауважимо, що для кожної з вибірок положення інтервалів групування дещо інше, що пояснюється тим, що кожний найменший та найбільший елементи різних вибірок різні.

Очевидно, що кількість потраплянь результатів у інтервали групування для кожної реалізації вимірювального експерименту є щораз іншою. Тому для одержання стійкої гістограми необхідно, щоб у кожен з інтервалів потрапляла достатньо велика кількість результатів. Це можливо за умови великого за обсягом експерименту – кілька сотень і більше результатів спостережень.

За формою гістограми чи полігона досвідчений експериментатор може зробити висновок про вид моделі густини розподілу випадкових величин.

Зрозуміло, що на основі скінченої кількості результатів спостережень, будуючи гістограми чи полігони, принципово неможливо точно визначити розподіл випадкової величини.

Отримані експериментально оцінки розподілів дають можливість лише пропонувати гіпотези про модель розподілу випадкової величини. У певних випадках під час аналізу гістограми (чи полігона) виникають певні сумніви щодо моделі розподілу. Доцільно було б мати також кількісні показники форми розподілу, зокрема наближеності чи віддаленості експериментального розподілу від теоретичного чи модельного, ступеня їхньої симетричності тощо. Серед таких показників широко застосовують коефіцієнти скошеності (асиметрії) s та сплющеності (ексцесу) , які створені з застосуванням таких характеристик як початкові і центральні моменти, зокрема так звані вибіркові моменти. Ця термінологія до випадкових величин перейшла з механіки.

Вибірковим початковим моментом α_r порядку r називають середнє значення r-го ступеня елементів вибірки:

, (2.29)

а вибірковим центральним моментом _r порядку r називають середнє значення r-го ступеня центрованих значень елементів вибірки (зміщених на середнє значення):

. (2.30)

Отже, перший початковий момент вибірки це її середнє значення:

. (2.31)

Теоретичні значення початкового М_r та центрального μ_r моментів випадкової величини знаходять із вибіркових за необмеженого зростання обсягу вибірки до генеральної сукупності і вони є невипадковими величинами.

Вибірковий центральний момент другого порядку та вибіркова дисперсія (2.5) пов'язані між собою залежністю

. (2.32).

Коефіцієнт скошеності (асиметрії) дорівнює відношенню третього центрального моменту розподілу ₃ до куба стандартного відхилення ³, а для експериментальної вибірки – відношенню відповідних вибіркових оцінок:

. (2.33)

Він характеризує несиметричність (скошеність) розподілу (наприклад, один бік розподілу пологий, а інший крутий, рис. 2.4, а). Оскільки для симетричних відносно свого центру розподілів всі непарні (в т. ч. третій) центральні моменти дорівнюють нулеві, то для симетричних розподілів коефіцієнт скошеності (асиметрії) дорівнює нулеві.

Характеристикою точності визначення коефіцієнта скошеності (асиметрії) може бути його нормоване стандартне відхилення, яке залежить лише від кількості результатів спостереження:

, (2.34)

тобто у першому наближенні зменшується пропорційно до квадратного кореня з обсягу вибірки.

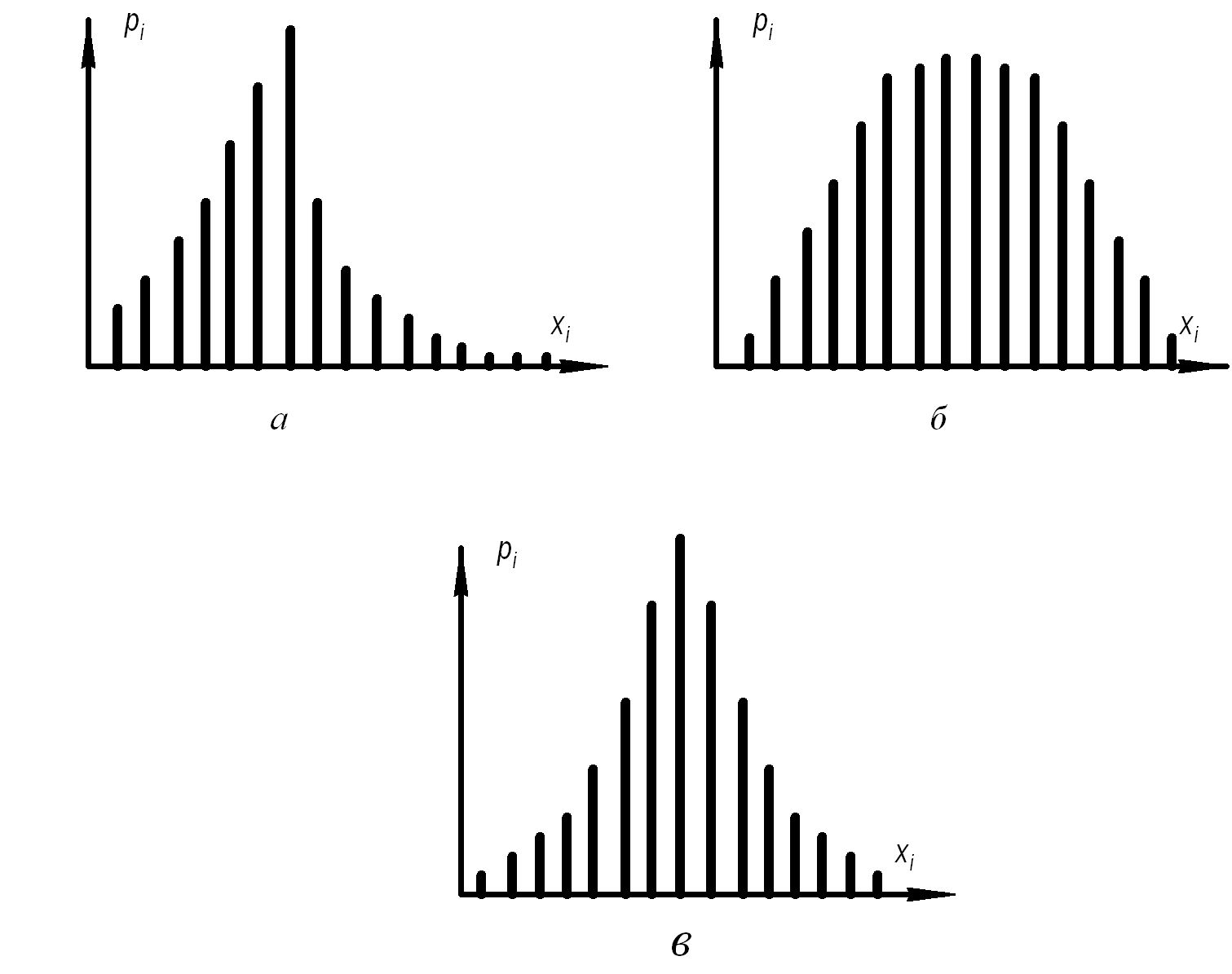
Рисунок. 2.4 ‑ Несиметричний (скошений) (а), сплющений (б) та витягнутий (в) розподіли

Коефіцієнт скошеності (асиметрії) вважають істотним, тобто розподіл істотно несиметричним, якщо виконується умова

. (2.35)

Коефіцієнт сплющеності (ексцесу) характеризує сплющеність розподілу (рис. 2.4, б) та протяжність його спадів. Він дорівнює (теоретично) зменшеному на три відношенню четвертого центрального моменту розподілу до четвертого ступеня стандартного відхилення , а для експериментальних вибірок – відношенню відповідних оцінок центральних моментів:

. (2.36)

Для означення коефіцієнта сплющеності (ексцесу) у (2.36) використано від'ємник 3, тому що для базового за формою нормального розподілу відношення . Оцінка сплющеності (ексцесу) за (2.36) є зміщеною на т_ = – 6/(n +1). Отже, розподіл, у якого коефіцієнт сплющеності (ексцесу) близький до нуля, з цього погляду близький до нормального.

Аналогічно як для коефіцієнта скошеності (асиметрії), характеристикою точності знаходження коефіцієнта сплющеності (ексцесу) може бути його нормоване стандартне відхилення:

, (2.37)

яке також у першому наближенні зменшується пропорційно до квадратного кореня з обсягу вибірки.

Аналогічно коефіцієнт сплющеності (ексцесу) вважають істотним, якщо виконується умова

. (2.38)

Якщо нерівності (2.35) та (2.38) виконуються, то вважають, що закон розподілу випадкової величини відрізняється від нормального.

Приклад 2.4 Для заданої у прикладі 2.2 просортованої вибірки 1_с визначити вибіркові оцінки коефіцієнтів асиметрії та ексцесу та оцінити їхню істотність.

Розв'язання. Для знаходження вибіркових оцінок цих коефіцієнтів використаємо розраховані у прикладі (2.2) значення вибіркових оцінок центральних моментів. Отже, пораховані за правою частиною формули (2.33) оцінка коефіцієнта асиметрії (скошеності) для першої вибірки становить s_к = 0,183.

Аналогічно, пораховані за правою частиною формули (2.36) оцінка коефіцієнта ексцесу (сплющеності) для першої вибірки становить _к =: 0,267.

Для обсягу вибірок п = 50 розраховуємо нормовані стандартні відхилення цих коефіцієнтів:

скошеності (асиметрії)

,

а також сплющеності (ексцесу)

.

Порівнюючи знайдені оцінки коефіцієнта скошеності (асиметрії) із допустимим значенням 3_s= 0,979, згідно з умовою (2.34) бачимо, що не можна вважати, що розподіл істотно асиметричний.

Порівнюючи знайдену оцінку коефіцієнта сплющеності (ексцесу) із допустимим значенням 3_ = 1,793 згідно з умовою (2.38) бачимо, що для вказаної вибірки немає підстав вважати, що розподіл істотно сплющений чи видовжений. Тобто за формою він цілком задовольняє форму нормального розподілу. Наявність скошеності (асиметрії) та сплющеності (ексцеси) вибіркових розподілів можна трактувати як результат обмеження розміру випадкових вибірок.