Понятие дифференцируемой функции в точке.
Дифференциал функции в некоторой точке – главная линейная часть приращения функции, равная произведению производной этой фунции в выбранной точке на приращение независимой переменной
Приращение функции и ее дифференциал являются эквивалентными бесконечно малыми величинами, их разность есть величина бесконечно малая более высокого порядка малости по сравнению с каждой из них ∆y ~ dy.
Формула вычисления дифференциала. Дифференциал функции у = f(x) в точке х0 равен произведению производной этой функциии f'x(x), вычисленной в точке х0, на приращение независимой переменной х.
dy = f'x(xo) • As, или dy = у|x (х0) • ∆x (1).
Согласно этой формуле дифференциал и приращение независимой переменной равны между собой, так как при у = х имеем j/ = х' = 1 и cit/ = dx = 1 • Дх s Дх. Итак, cfx = Дх. Тогда формула вычисления дифференциала примет такой вид
dy = f'x(x0)-dx, или dy = y'x(x0) - dx . (2)
Формулы (1) и (2) нахождения дифференциала равнозначны.
9.
Найдите d2y
10.
Найти
или
для функции заданной параметрически.
Если
функция аргумента x
задана параметрически
,
где
и
-
дифференцируемые функция.
Причем
.
Тогда производная этой функции по переменной x вычисляется по формуле:
,
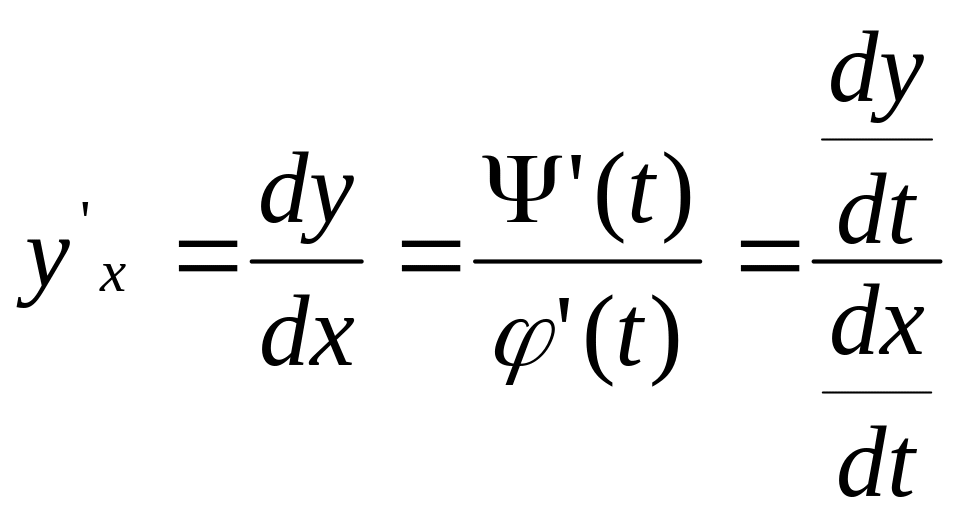Докозательство:
Предположим,
что
и
дифференцируемы и
имеет
обратную функцию
тоже
дифференцируема.
Тогда
,
считаем t
промежуточным
аргументом.
Продифференцируем
функцию
Итак,
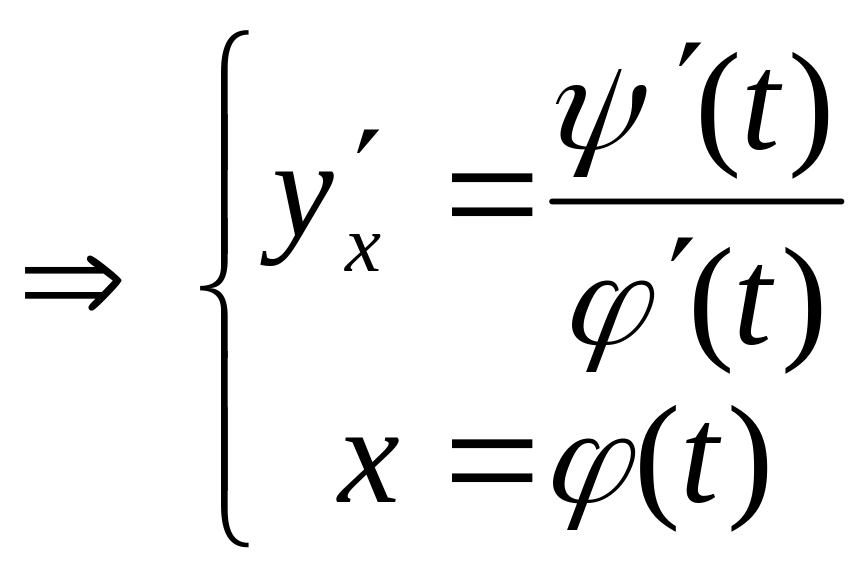
14
Второй достаточный признак локального экстремума функции:
Пусть
f(x)
2n
рода диффер в (∙)Xo
причем 1)
2)
Тогда f(x)
имеет екстремм в (∙)Xo,
причем Xo-(∙)лок
max,
если
и
Xo-(∙)лок
min
если
Д
Пусть
для определ
Представим f(x)
в окрестности(∙)Xo
по формуле Тейлора
где
-ограниченна
U(Xo,δ)
любое X
пренадлежит U(Xo;
δ)
