145. Функции двух переменных

Функция - фундаментальное понятие математического анализа: переменная y является функцией переменной x, если по некоторому правилу или закону каждому значению x из X соответствует одно определенное значение y из Y.

Пусть каждой упорядоченной паре чисел (х, у) из некоторой области D(x, y) соответствует определенное число z є R. Тогда z называется функцией двух переменных х и у, х, у – независимыми переменными или аргументами, D – областью определения или существования функции, а множество Е всех значений функции – областью ее значений. Символически функция двух переменных записывается в виде равенства z=f(x, y), в котором f обозначает закон соответствия. Этот закон может быть задан аналитически (формулой), с помощью таблицы или графика.

Так как всякое уравнение z=f(x, y) определяет, вообще говоря, в пространстве, в котором введена декартова система координат Oxyz, некоторую поверхность, то под графиком функции двух переменных понимают поверхность, образованную множеством точек M(x, y, z) пространства, координаты которых удовлетворяют уравнению z=f(x, y)

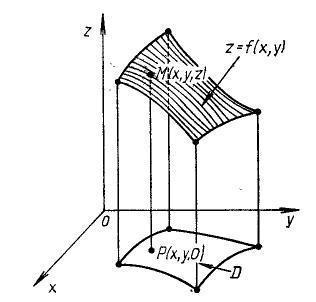
Геометрически область определения функции D обычно представляет собой некоторую часть плоскости Оху, ограниченную линиями, которые могут принадлежать этой области. В первом случае область D называется замкнутой и обозначается , во втором – открытой.

Число А называют пределом функции z=f(x, y) в точке М0(х0, у0), если для любого ε>0 существует d>0, такое, что при всех х, у, удовлетворяющих условиям |x-x0|<d и |y-y0|<d, справедливо неравенство |f(x, y)-A|< ε. Если А – предел функции f(x, y) в точке М0(х0, у0), то пишут:

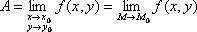
Функция z=f(x, y) называется непрерывной в точке М0(х0, у0),если справедливо равенство А= f(X0, Y0).

Например, функция z=1/(2x2+y2) непрерывна в любой точке плоскости, за исключением точки М(0, 0), в которой терпит бесконечный разрыв.

Функция, непрерывная во всех точках некоторой области D, называется непрерывной в данной области.

Если переменной х дать некоторое приращение Dх, а у оставить постоянной, то функция z=f(x, y) получит приращение Dхz, называемое частным приращением функции z по переменной х:

Dхz=f(x+Dx, y) – f(x, y).

Аналогично, если переменная у получает приращение Dу, а х остается постоянной, то частное приращение функции z по переменной у

Dуz=f(x, y+Dу) – f(x, y).

Например, функция z=1/(2x2+y2) непрерывна в любой точке плоскости, за исключением точки М(0, 0), в которой терпит бесконечный разрыв.

Если существуют пределы:

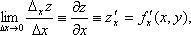
они называются частными производными функции z=f(x, y) по переменным х и у соответственно.

Дифференциал функции z=f(x, y), найденный при условии, что одна из независимых переменных изменяется, а вторая остается постоянной, называется частным дифференциалом, т.е. по определению

dxz=f’x(x, y)dx, dyz=f’y(x, y)dy,

где dx=∆x, dy=∆y – произвольные приращения независимых переменных, называемые их дифференциалами. Это справедливо и для функции трех переменных w=f(x, y, z).

146. Функции переноса, поворота и масштабирования и их параметры в OpenGl

OpenGL - это программный интерфейс (API) для разработки приложений с использованием 2D и 3D графики. Основными особенностями библиотеки являются:

Стабильность. Это подразумевает то, что новые дополнения к ядру OpenGL реализуются так, что бы сохранить совместимость с более старыми версиями.

Переносимость (независимость). Код программы, которую вы написали, скажем, под Windows, можно легко перенести на Linux и другие ОС. То есть, OpenGL не зависит от какой нибудь операционной системы, как, например DirectX.

Простота в использовании. Приложения, написанные с помощью OpenGL, имеют сравнительно небольшой объем кода. Также эта библиотека имеет понятный интерфейс и читабельность кода.

Важно то, что OpenGL - это отраслевой стандарт, поэтому вы можете воспользоваться исходными кодами и делать на их основе собственные разработки.

Все преобразования объектов и камеры в OpenGL производятся с помощью умножения векторов координат на матрицы. Причем умножение происходит на текущую матрицу в момент определения координаты командой glVertex* и некоторыми другими.

Для задания различных преобразований объектов сцены в OpenGL используются операции над матрицами, при этом различают три типа матриц: модельно-видовая, матрица проекций и матрица текстуры. Все они имеют размер 4x4. Видовая матрица определяет преобразования объекта в мировых координатах, такие как параллельный перенос, изменение масштаба и поворот. Матрица проекций определяет, как будут проецироваться трехмерные объекты на плоскость экрана (в оконные координаты), а матрица текстуры определяет наложение текстуры на объект.

Умножение координат на матрицы происходит в момент вызова соответствующей команды OpenGL, определяющей координату (как правило, это команда glVertex*)

Для того чтобы выбрать, какую матрицу надо изменить, используется команда: