Движение материальной точки по окружности

1.203.На сколько километров орбита первого спутника Земли короче орбиты третьего спутника, если средние радиусы их орбит отличаются на ΔR=410 км?

1.204.Найти линейную скорость Луны, обусловленную ее обращением вокруг Земли. Период вращения Луны (синодический месяц) Т=27,3 сут. Расстояние Земля-Луна R=3,84*10⁵ км.

1.205.Корабль-спутник «Восток-5» с космонавтом Николаевым на борту совершил N=64 оборота вокруг Земли за t=95 ч. Определить среднюю скорость полета v. Орбиту корабля можно считать круговой и отстоящей от поверхности Земли на h=230 км.

1.206.Равномерно движущаяся по окружности точка делает полный оборот за Т=5 с. Чему равна угловая скорость точки ω? Чему равен угол поворота точки Δφ за время Δt=2 с?

1.207.Скорость точек рабочей поверхности шлифовального круга не должна превышать v=100м/с. Найти предельную частоту вращения круга n, диаметр которого d=40 см. Определить нормальное ускорение а_n точек рабочей поверхности круга.

1.208.Большой шкив ременной передачи имеет радиус R₁=32 см и вращается с частотой n₁=120 об/мин. Малый шкив имеет радиус R₂=24 см. Найти угловую скорость, число оборотов в секунду малого шкива и линейную скорость точек ремня, который движется без проскальзывания.

1.209.Диск равномерно вращается относительно оси, проходящей через его центр и ему перпендикулярной. Линейная скорость точек края диска v₁=3 м/с. У точек, расположенных на расстоянии l=10 см ближе к оси, скорость v₂=2 м/с. Какова частота n вращения диска?

1.210.Найти радиус R вращающегося колеса, если известно, что линейная скорость точек обода колеса в k=2,5 раза больше линейной скорости точки, лежащей на расстоянии d=5 см ближе к оси колеса.

1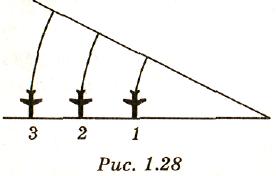 .211.Ось с двумя дисками, расположенными на расстоянии l=0,5 м друг от друга, вращается с частотой n=1600 об/мин. Пуля, летящая вдоль оси, пробивает оба диска: при этом отверстие от пули во втором диске смещено относительно отверстия в первом диске на угол φ=12°. Найти скорость пули v.

1.212.Найти линейную скорость v и нормальное ускорение а_n точек . земной поверхности на: а)экваторе; б)географической широте φ=60°, обусловленные вращением Земли вокруг своей оси.

1.213.Три самолета выполняют разворот в горизонтальной плоскости, двигаясь по траекториям, которые показаны на рисунке 1.28, на расстоянии l=60 м друг от друга. Ближайший к центру виража самолет движется по окружности радиусом R=600 м. Средний самолет движется со скоростью v₂=360 км/ч. Найти ускорение каждого самолета.

1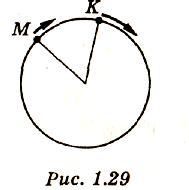 .214.Две точки М и К движутся по окружности (рис. 1.29) с постоянными угловыми скоростями ω_M=0,2 рад/с, ω_K=0,3 рад/с. В начальный момент времени угол между радиусами этих точек равен π/3. В какой момент времени t точки встретятся?

1.215.Кошка бежит за мышкой по окружности радиусом R=5м с постоянной скоростью v_K=40 км/ч. Когда расстояние по дуге между ними было равно 1/8 длины окружности, мышка начала убегать со скоростью v_M=50 км/ч. Через какое время t мышка удалится от кошки на расстояние, равное половине длины окружности?

1 .216.Две точки равномерно движутся по окружности. Первая точка, двигаясь по часовой стрелке, делает один оборот за Т₁=5 с, вторая точка, двигаясь против часовой стрелки, делает один оборот за Т₂=2 с. Найти время t между двумя последовательными встречами точек.

1.217.Сколько раз N в сутки встречаются часовая и секундная стрелки часов?

1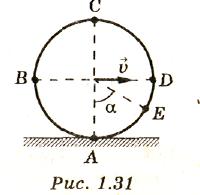 .218.Две точки одновременно начали движение с одинаковой постоянной скоростью v=0,5 м/с; одна по окружности радиуса r= 5 м, другая по окружности радиуса R=10 м (рис. 1.30). Найти угол между направлениями ускорений точек через время t=1 мин после начала движения, если в начальный момент точки находились на одном радиусе.

1.219.Небольшое тело движется по окружности радиуса R=1 м. Определить модуль перемещения за время, в течение которого тело делает: а)оборот; б)1/2 оборота; в)1/4 борота; г)тело поворачивается на угол α=60°.

1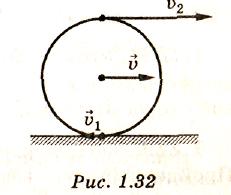 .220.За промежуток времени Δt=10 с тело прошло половину окружности радиуса R=100 см. Найти среднюю путевую скорость v и модуль средней скорости v_ср.

1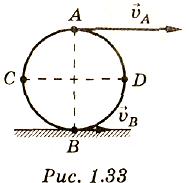 .221.Однородный диск радиусом R=0,5 м катится без проскальзывания со скоростью v=2 м/с. Найти скорость точек диска A, В, С, D, E (рис. 1.31). Найти геометрическое место всех точек диска, скорость которых v=2 м/с. Угол α=60°.

1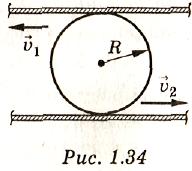 .222.Колесо, пробуксовывая, катится по ровной, горизонтальной дороге. Найти скорость центра колеса v (рис. 1.32), если известно, что скорость его нижней точки v₁=2 м/с, а верхней - v₂=10 м/с.

1.223.Обруч, проскальзывая, катится по горизонтальной поверхности (рис. 1.33). В некоторый момент времени скорость верхней точки А v_A=6 м/с, а нижней точки В v_B=2 м/с, Определить скорость концов диаметра CD, перпендикулярного к АВ, для того же момента времени. Под какими углами они направлены к горизонту?

1.224.Цилиндр радиуса R зажат между движущимися со скоростями v₁ и v₂ параллельными рейками (рис. 1.34). С какой угловой скоростью вращается цилиндр? Проскальзывания нет.

1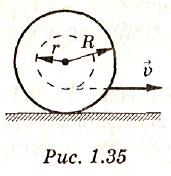 .225.Катушка с намотанной на ней нитью лежит на горизонтальном столе и может катиться по нему без скольжения. Внешний радиус катушки R, внутренний r (рис. 1.35). С какой скоростью v₀ и в каком направлении будет перемещаться ось катушки О, если конец нити тянуть в горизонтальном направлении со скоростью v? Как изменится ответ, если нить будет сматываться сверху?

1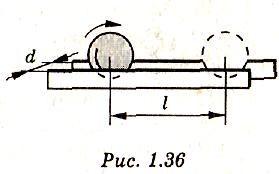 .226.Шарик радиуса R=5 см катится равномерно и без проскальзывания по двум параллельным линейкам, расстояние между которыми d=6 см (рис. 1.36), и за время t=2 с проходит расстояние l=120 см. С какими скоростями движутся верхняя и нижняя точки шарика?

1.227*.Автомобиль движется по закругленному шоссе, имеющему радиус кривизны R=40 м. Закон движения автомобиля имеет вид s=А+Bt+Ct², где А=5 м; В=12 м/с, С=-0,5м/с². Найти скорость автомобиля и, его тангенциальное а_τ, нормальное а_n и полное а ускорения в момент времени t=4 с.

1.228*.Угол поворота диска радиусом R=10см изменяется со временем по закону φ=4+2t-t³. Определить зависимости от времени угловой скорости, углового ускорениям линейной скорости точек диска.

1.229.Материальная точка движется по окружности радиуса R=10 см. Пройденный путь зависит от времени по закону l=At, где А=1 м/с. Найти линейную и угловую скорости, ускорение точки и число оборотов, сделанных ею за первые 5 с после начала движения.

1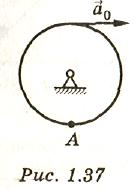 .230.Точка движется по окружности с постоянным угловым ускорением ε=1 рад/с². Найти угол между скоростью и ускорением через t=1 с после начала движения. Начальная скорость точки (при t₀=0) v₀=0

1.231.Частица начинает двигаться по окружности с постоянным тангенциальным ускорением. Найти угол между скоростью и ускорением после первого оборота. Начальная скорость точки равна нулю.

1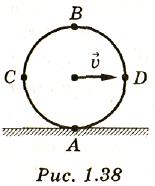 .232*.Точка движется по окружности радиуса R=2 м по закону φ=2+2t-t². Определить путь l, пройденный точкой до остановки. Определить ускорение точки в момент времени t_l=0,5 с.

1.233.По окружности радиуса R=2 м одновременно движутся две точки так, что законы их движения имеют вид: φ₁=2+2t и φ₂=-3-4t. Определить относительную скорость и в момент их встречи.

1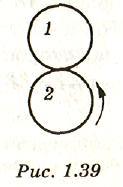 .234*.Шкив радиусом R=0,5 м приводится во вращение с помощью веревки, намотанной на него (рис. 1.37). Конец веревки тянут с ускорением а₀=0,1 м/с². Найти нормальное а_n, тангенциальное а_τ и полное ускорение нижней точки A шкива спустя t=2 с после начала вращения.

1.235*.Скорость центра колеса, катящегося без проскальзывания по горизонтальной поверхности (рис. 1.38), изменяется со временем по закону v=1+2t. Радиус колеса R=1 м. Найти скорости и ускорения четырех точек А, В, С, D колеса, лежащих на концах взаимно перпендикулярных диаметров, один из которых горизонтален, в момент времени t=0,5 с.

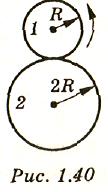
1 .236°.Два одинаковых диска расположены так, как показано на рисунке 1.39. Диск 1 неподвижен, а диск 2 вращается без проскальзывания относительно диска 1. На какой угол α повернется диск 2, обойдя один раз диск 1?

1.237°.У диска 1 радиус R, у диска 2 радиус в два раза больше (рис. 1.40). Диск 2 неподвижен. Сколько оборотов N без проскальзывания сделает диск 1, обойдя один раз диск 2?

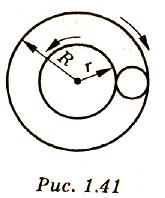
1.238°.Два концентрических колеса радиусами R=50 см и r=25 см вращаются в противоположные стороны с угловыми скоростями ω₁=5 рад/с и ω₂=10 рад/с соответственно. Между ними зажато третье колесо так, как показано на рисунке 1.41. Какова угловая скорость вращения этого колеса вокруг собственной оси? Проскальзывания нет.