19

Тема №7

Векторные и матричные нормы.

Обусловленность СЛАУ. Число обусловленности матрицы.

Вычисление определителей. Обращение матриц.

Ортогональные преобразования.

Матрицы вращения и отражения. QR- и HR-разложения матриц.

Метод ортогонализации. Метод отражений

7.1 Векторные и матричные нормы

Норма (абсолютная величина, модуль вектора) вектора:

;  вещественное число :

1. и тогда и только тогда, когда ,

2. для любого числа и любого .

3. – неравенство Минковского.

Норма матрицы:

1.

2.

3.

Определение 1. Данная норма матриц называется согласованной с данной нормой векторов, если для любой матрицы A и для любого вектора справедливо неравенство

Определение 2.

– вектор погрешности,

– точное решение системы ,

– результат вычислений .

Определение 3.

– вектор невязки.

Малость вектора невязки необходима для того, чтобы вычисленные значения неизвестных были близки к точным, но не достаточна



и .

Если – мал, то – мал, если норма обратной матрицы мала,

– большой, если норма матрицы велика

(наблюдается у плохо обусловленных матриц),

7.2. Обусловленность систем линейных уравнений

Обусловленность вычислительной задачи – чувствительность ее решения к малым погрешностям входных данных

.

где : – погрешность входных данных,

– погрешность решения,

– абсолютное число обусловленности,

( ) – относительное число обусловленности.

, N – число верных цифр

– ?

– !

Оценка обусловленности



Возмущенная СЛАУ: .

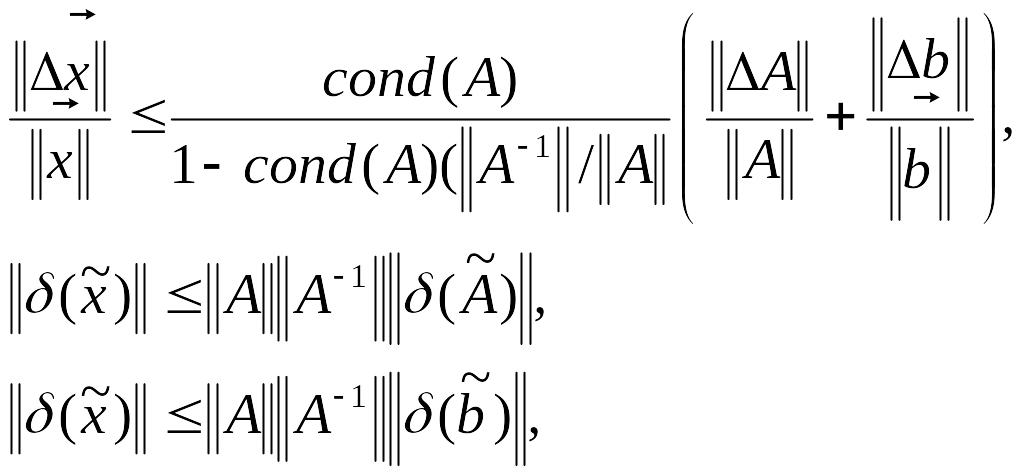
где

Определение 4.

– стандартное число обусловленности матрицы.

Свойства cond(A) :

1. cond(E) =1.

2. cond(A)1.

3. cond(AB)cond(A)cond(B) .

7. Число обусловленности не меняется при умножении матрицы A на ненулевое число.

7. Для симметрической матрицы A :

Вычисление = нахождение и = n³+2n² операций

Определение 5.

– велико: матрица A – плохо обусловленная,

– мало: матрица A – хорошо обусловленная.



Не существует численного метода, с помощью которого можно было бы устранить чувствительность плохо обусловленной системы к возмущениям элементов матрицы и правой части

Грубая оценка .

Если , то .  .

Эвристически: если выбирать случайно, то  .

Решение систем линейных уравнений с плохо обусловленными матрицами – некорректная задача

Рис.1

Пример. Матрица Гильберта A; – плохо обусловленная матрица.

Таблица 7.1

Порядок матрицы Гильберта	2	3	4	5	6	7	8	9	10
Приближенное значение cond(A)	2101	5102	2104	5105	2107	5108	21010	51011	21013

Различают:

- плохо обусловленные задачи – задачи, в которых малые погрешности во входных данных (в том числе и во время промежуточных вычислений) вызывают большие погрешности решения,

- плохо обусловленные вычисления – результат применения численно неустойчивых методов.