1.4.3. Деформаційні критерії руйнування. -критерій

У більшості випадків руйнування металів супроводжується попереднім розвитком пластичних деформацій біля концентраторів напружень. М.Я. Леонов, В.В. Панасюк і Д.С. Дагдейл запропонували критерії, які дають змогу визначити розмір пластичної зони і розкриття вістря тріщини у пружно-пластичному тілі. Ці критерії дістали назву деформаційно-енергетичних або -критеріїв.

Таблиця 1.3

Вигляд функцій, що враховують розміри пластини, форму тріщини та спосіб навантаження при визначенні КІН

Вид навантаження	Схема	Функція форми та розмірів об’єкта
Розтяг необмеженої пластини з похилою тріщиною в середині Розтяг або згин у її площині, смуги з однобічною тріщиною Розтяг смуги з поперечною тріщиною посередині Розтяг смуги з двома боковими тріщинами Згин у площині смуги з поперечною тріщиною посередині		. . . . - наближена формула Б.Л.Лозового та В.В.Панасюка для , (похибка <3%).

Згідно з -критерієм вважають, що умовою руйнування матеріалу може бути досягнення величини розкриття тріщини (рис. 1.11, а) її критичного значення :

, (1.29)

де – константа матеріалу, яка фіксується у момент початку руху тріщини; – граничне значення деформації, за якої відбувається розрив матеріалу; – певна початкова довжина елемента матеріалу в зоні передруйнування (рис. 1.11, б).

Рис. 1.11. Розрахункова схема для матеріалу на продовженні тріщини (а) та спосіб визначення розкриття тріщини (б)

Вважається, що в процесі деформування матеріал може знаходитись у трьох станах: суцільному (С-стані), зруйнованому (Р-стані) та певному проміжному (П-стані), яким супроводжується Р-стан. Зону, у якій матеріал знаходиться у П-стані, називають зоною передруйнування. Тут матеріал деформується за границею пружності, де відбувається його інтенсивна пластична плинність та подальше локальне руйнування. Така умовна зона моделюється розрізом на продовженні тріщини, на берегах якого діють усереднені напруження . Ці напруження, залежно від моделі матеріалу, знаходяться у межах і є інтегральною характеристикою міцності матеріалу на відрив. Їх визначають з умови рівновеликості площ, що обмежуються істинною (крива 1) та модельною (ламана 2) діаграмами деформування (рис. 1.12).

Р ис. 1.12. Графічне визначення напруження

Фактично ця умова є умовою рівності енергій руйнування реального тіла та моделі. До досягнення величини зв'язок між напруженнями та деформаціями у матеріалі описується лінійним законом Гука. Напруження на берегах тріщини вважаються нульовими, якщо розкриття тріщини перевищує величину . У рамках прийнятої моделі для даного пружно-пластичного матеріалу та закону розподілу інтенсивності сил зчеплення між сусідніми атомами величини , зв’язані з густиною енергії руйнування залежністю

. (1.30)

Умови (1.29), (1.30) є основними умовами -критерію, що зводять нелінійну задачу для крихкого тіла з тріщинами до розв’язку задачі лінійної теорії пружності з додатковими характеристиками реального матеріалу.

Довжину самої зони передруйнування у вигляді пластичної зони нульової товщини, що знаходиться на продовженні осі тріщини, вперше визначив Д. Даґдейл (1960 р.). Пізніше Б. Кудрявцевим та іншими авторами (1970 р.) розміри цієї зони були уточнені для пластини необмежених розмірів за допомогою теорії малих пружно-пластичних деформацій у вигляді формули

. (1.31)

Враховуючи вираз та формулу (1.31), одержимо

. (1.32)

Тоді, з урахуванням пластичної зони, половину довжини тріщини із зоною зчеплення у її кінчику можна записати у вигляді

. (1.33)

Така поправка дає можливість застосувати критерій Ірвіна навіть у нелінійних задачах, підставивши у відповідні формули замість величини величину . При цьому необхідно пам’ятати, що розміри пластичної зони при плоскій деформації набагато менші, ніж при плоскому напруженому стані.

У найпростішому випадку навантаження нескінченної пластини розподіленим навантаженням (рис. 1.11, а) В.Панасюк одержав

. (1.34)

Розклавши приведену функцію в ряд та обмежившись першим членом (за умови, що ), отримаємо

. (1.35)

Із критерію (1.29) та формули (1.35) легко отримати вираз для граничного напруження

. (1.36)

Підставивши у формулу (1.36) залежність (1.30), отримуємо відповідний критерій А. Ґріффітса (1.20). Проте останній дає при фізично нереальний результат (тобто міцність матеріалу є безмежно великою). Одночасно, для - критерію ця умова означає, що (тобто тіло з тріщиною нульової довжини має міцність бездефектного середовища).

-критерій сприяв формулюванню близького за ідеологією критерію КРТ (критичного розкриття тріщини), одного з найбільш використовуваних у нелінійній механіці руйнування. Цей критерій був остаточно сформульований А. Уеллсом у 1963 році.

За реалізації інших механізмів зміщення берегів тріщини (поперечний та поздовжній зсуви) критеріальні рівняння аналогічні попередньому:

. (1.37)

Між базовими характеристиками критеріїв , і , а також , і існує взаємозв’язок, що випливає із відомих розв’язків В.Панасюка, О.Андрейківа, М.Саврука та ін. для відповідних пружних задач:

; ; , (1.38)

де у випадку ідеально-пружно-пластичного матеріалу приймається, що , а .

У рамках -критерію В. Панасюком, Я. Іваницьким та А. Андрейківим розроблено узагальнений критерій руйнування тіла (1985 р.) у випадку можливої одночасної реалізації трьох макромеханізмів руйнування . Отримано наближене критеріальне рівняння для визначення критичного розміру довжини тріщини

, (1.39)

яке пізніше (2000 р.) було уточнене (для ізотропних матеріалів) детермінізацією показників степенів для всіх трьох відношень КІН.

Головним недоліком -критерію є те, що він експериментально підтверджується тільки для ідеально пластичних ізотропних матеріалів при одному із напружених станів. Якщо матеріал не ізотропний і можлива реалізація всіх трьох макромеханізмів руйнування, то необхідно вводити інші параметри матеріалу, які визначаються експериментально. Крім того, безпосереднє експериментальне визначення параметра 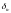можливе тільки при застосуванні лінійної механіки руйнування. Хоча якісні висновки -критерію можна поширити і на дуже в’язкі матеріали, російський механік Ю.М.Работнов піддав сумніву твердження, що величини можна вважати універсальними сталими матеріалу.