1.4. Критерії руйнування матеріалів із тріщинами

1.4.1. Крихке руйнування. Критерій Ґріффітса

Міцність твердого деформівного тіла з крихкого матеріалу значною мірою залежить від наявності в ньому великої кількості дефектів типу мікротріщин, що є впливом як самої мікроструктури матеріалу, так і технології його обробки. Це і наявність включень з іншого матеріалу, дефектів, спричинених відпускною крихкістю або неправильно проведеного цементування. Дефекти можуть виникати також внаслідок неправильної механічної обробки, або в процесі експлуатації через надмірне тертя та зношування. Наявність дефектів і, зокрема, тріщин у конструкціях, створює загрозу раптового руйнування або значно зменшує її міцність і ресурс.

У зв’язку із названими факторами виникає необхідність поряд із критеріями міцності, що не передбачають наявності тріщин, формувати і користуватись критеріями руйнування, що враховують наявність, характер та вплив мікро- і макротріщин на руйнування матеріалів за напружень, які можуть бути нижчими за границю міцності (або навіть за границю плинності).

Вперше такий критерій був сформульований англійським інженером А. Ґріффітсом (1920 р.), згідно якого тріщина починає рости в деформованому крихкому тілі за такого напруженого стану 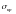, за якого швидкість вивільнення енергії пружної деформації тіла , під час її поширення, перевищує приріст поверхневої енергії тіла на нових поверхнях тріщини, тобто настане рівність

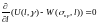. (1.14)

При цьому, вважається, що величина пропорційна приросту поверхні утвореної тріщини та величини питомої густини поверхневої енергії 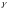, яка чисельно дорівнює енергії, необхідної для утворення одиниці площі нової вільної поверхні -

, (1.15)

де – довжина тріщини.

Для підтвердження цього припущення була розглянута нескінченна пластинка одиничної товщини, що розтягувалась рівномірним навантаженням перпендикулярно до тріщини довжиною (рис. 1.7). Необхідно було знайти напруження , при досягненні якого тріщина почне рухатися. Таке напруження називають граничним або критичним. Довжина тріщини, при якій досягається таке напруження, називається критичною довжиною .

Якщо пластина знаходиться у лінійному напруженому стані, то вираз для питомої потенціальної деформації має вигляд:

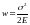. (1.16)

Поява у такій пластині тріщини призводить до деякого зниження поля напружень у її околі, величину якого приймаємо рівною площі круга з радіусом .

Рис. 1.7. Розподіл напружень у пластині з еліптичною тріщиною(а); графічна залежність між граничним напруженням і критичною довжиною тріщини (б)

Вважатимемо, виходячи з принципу Сен-Венана, що та частина потенціальної енергії, котра припадає на зону зменшення напружень у пластинці з тріщиною і на яку зменшується повна енергія пластинки, буде дорівнювати:

(1.17)

Результат (1.16) відповідає точному розв’язку Інгліса (1913 р.) для площини з еліптичним отвором, що має більшу вісь довжиною 2l (менша вісь спрямовується до нуля).

За енергетичним критерієм граничної рівноваги тріщини (1.14), у граничному стані зменшення потенціальної енергії деформації повинно дорівнювати витраті питомої поверхневої енергії на прирості довжини тріщини 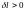, тобто воно еквівалентне виразу

, (1.18)

де

.

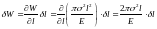
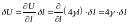Тоді з умови (1.18) отримуємо

. (1.19)

З формули (1.19) визначимо граничне напруження :

. (1.20)

За формулою (1.20) можна визначити критичне напруження 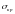, прикладене до пластини, при якому відбувається самочинне, без додаткової роботи зовнішніх сил, поширення тріщини початкової довжини 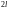. Фактично величина визначає міцність матеріалу за даної довжини тріщини, тому її ще називають залишковою міцністю. Очевидно, що відрізняється (у меншу сторону) від міцності на розрив однорідного матеріалу. Для випадку плоского деформованого стану у формулі (1.20) модуль пружності 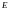необхідно замінити величиною .

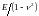Формулу (1.20), яка перевірялась А. Ґріффітсом експериментально, можна ще записати у вигляді залежності

, (1.21)

Для скляних колб та циліндричних трубок середнє значення цієї величини дорівнювало 262 .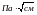

Одним із формальних недоліків формули (1.20) вважається, що відповідно до неї, міцність тіла з тріщиною мікроскопічної довжини є нескінченно великою (рис. 1.7, б). Однак вона не може перевищувати відповідні граничні напруження однорідного тіла. Цього недоліку можна легко позбутися, якщо допустити наявність у матеріалах початкових мікротріщин завдовжки 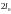, котрі відповідають певним значенням міцності . Такі допущення дещо узагальнюють критерій А. Ґріффітса, водночас ускладнюючи його використання через відсутність (у більшості випадків) названих параметрів.

Із формули (1.20) за заданого рівня критичних напружень можна знайти також критичну довжину тріщини:

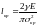. (1.22)

Виходячи з цієї формули, можна зробити висновок, що поява тріщини в тілі конструкції може призвести до її руйнування тільки у разі досягнення критичної довжини тріщини. Графічна залежність між ними подана на рис. 1.7, б. Аналіз цієї залежності та практичний досвід розрахунків свідчить, що для тріщини з критичним напруженням, більшим від 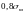, задача теорії пружності стає нелінійною, тому формула (1.20) уже не може вважатися точною, і в таких випадках необхідно користуватись іншими методами.

Зауважимо, що експерименти, проведені самим А. Ґріффітсом для перевірки запропонованого ним критерію, отримали підтвердження тільки для такого ідеально крихкого матеріалу, як скло. Експерименти, проведені для сталей, дали негативні результати. Пояснення цьому фактові дали тільки через 25 років англійські механіки Е.Орован та Дж.Ірвін, які припустили, що у квазікрихких матеріалах, подібних до сталей, у зоні вершини тріщини з’являється деяка зона пластичних деформацій, що інтенсивно поглинає вивільнену енергію і цим самим уповільнює рух тріщини. У зв’язку з цим ними була додатково врахована питома енергія 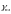, що затрачається на пластичне деформування шару металу поблизу поверхні тріщини:

,

яка стала використовуватись у формулах (1.20), (1.21) замість .

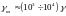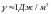Експериментально встановлено, що для металів . Наприклад, для сталі , а 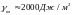. Отже, із достатньою точністю формулу (1.20) можна записати у вигляді:

. (1.23)

Зазначимо, що внаслідок істотної відмінності у кількості енергії, витраченої на руйнування крихких і квазікрихких матеріалів, можна стверджувати, що для просування тріщин у квазікрихких (а також в’язких) матеріалах необхідно додатково враховувати енергію пластичного деформування 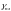. Тоді як для просування тріщин у крихких матеріалах цілком вистачає потенціальної енергії деформації, що є у конструкції.

Що таке математична модель тріщини? Розвиток тріщин зазвичай не супроводжується дуже вже великими деформаціями, але вона є головною причиною руйнування. В залізобетоні помітити тріщину навіть досить великої довжини не так уже й просто – тріщини стають помітними при навантаженнях, які значно перевищують експлуатаційні. Реальна тріщина (рис.1.8) в тілі включає в себе: 1 – фронт тріщини, де сходяться береги тріщини 2 – границі, показаної на рисунку порожнини 3.

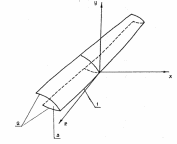
Рис. 1.8. Об’ємна модель тріщини

В околі фронту тріщини концентрація напружень буде найбільшою, а значить, саме у цьому місці відбудеться руйнування матерілу. Береги тріщин відіграють роль додаткової границі тіла, причому з-за малої відстані між ними реальну тріщину можна розглядати як математичний розріз, інакше кажучи, порожнину нульового об’єму, обмежену берегами розрізу, що є двома геометрично співпадаючими поверхнями.