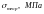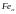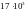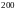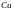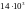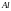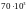1.3. Теоретична та реальна міцність твердих тіл

Міцність, жорсткість і пластичність твердих тіл є визначальними характеристиками, які необхідні конструктору при проектуванні деталей машин та елементів конструкцій. Міцність будь-якого твердого тіла забезпечується силами притягання (на відстанях x порядку 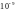м) між атомами у кристалічних ґратках (крива 2 на рис. 1.2).

Разом з тим, при силовому зближенні атомів до відстаней 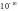м між ними виникають сили відштовхування (крива 3). Тому при зміні механічної рівноваги атома його напружений стан буде визначатися рівнодійною цих сил (крива 1), яку наближено можна записати у вигляді формули

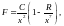(1.4)

д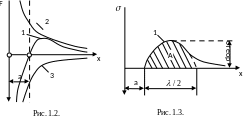 е С – стала бездефектного кристала; 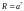; 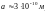– відстань між атомами кристала у рівноважному стані, – абсолютне зміщення у кристалічній ґратці при деформації в’язей. Для ненавантаженого тіла рівнодійна F дорівнює нулю.

Під теоретичною міцністю будемо вважати таке напруження , яке необхідно прикласти, щоб зруйнувати ідеальний кристал, тобто перебороти сили в’язей між атомами у ґратці. Таке руйнування можна здійснювати двома способами: відривом (через нормальне напруження) та зсувом (під дією дотичного напруження).

Більшість науковців вважає, що сили взаємодії атомів мають синусоїдальну залежність від зміни відстані між ними з певним періодом 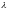(рис. 1.3). Тобто, величину нормального напруження в кристалічній ґратці можна апроксимувати синусоїдою:

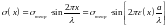, (1.5)

де – теоретична міцність матеріалу, 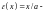відносна лінійна деформація.

Разом з тим, у зоні пружних деформацій має виконуватися закон Гука

. (1.6)

Продиференціюємо рівності (1.5) і (1.6) за змінною та прирівняємо їх при 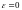, вважаючи, що у цьому випадку величина :

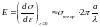. (1.7)

Звідки отримаємо

. (1.8)

З іншого боку, у відповідності до підходу Е.Орована (1949 р), робота А, яку необхідно затратити на розрив міжатомних в’язей, дорівнює площі під кривою (рис. 1.3), що апроксимує зміну напруження . Ця робота має дорівнювати питомій поверхневій енергії , що затрачується на утворення двох поверхонь тріщини в кристалі:

,

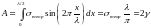звідки 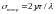. (1.9)

Перемноживши формули (1.8) і (1.9), отримаємо відому формулу Е.Орована:

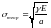, (1.10)

яка (за своєю ідеологією) ідентична формулі А. Ґріффітса (1.20) і дозволяє розглядати характер руйнування матеріалів із позицій тріщиноутворення.

Застосуємо цю формулу до сталі, коли:

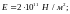
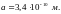
Тоді

Аналогічним способом можна отримати і величину теоретичного дотичного напруження, якщо прийняти .

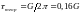. (1.11)

Детальніші дослідження інших науковців показують, що формула Е.Орована (1.10) дає дещо завищені значення (зберігаючи порядок) для теоретичного напруження, яке може знаходитись у межах:

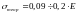. (1.12)

Останнє співвідношення підтверджує правильність попередніх міркувань. Разом з тим, реальна міцність матеріалів виявляється нижчою від теоретичної приблизно на 2 порядки (табл. 1.2). Фізики припускають, що причиною розходжень теоретичної і реальної міцності є те, що в основі теоретичних розрахунків є ідеальний кристал, а в реальному кристалі завжди присутні дефекти кристалічної будови.

Таблиця 1.2.

Метал	Механічні властивості

Вперше ці припущення експериментально підтвердив А. Ґріффітс (1920 р.), який досліджував скляні волокна. Так, волокно діаметром 1 мм мало міцність віконного скла – 0,15...0,2 ГПа, а волокно діаметром 0,25 мкм – 6 ГПа, яка через кілька годин спадала до 3,5 ГПа. Екстраполюючи отримані результати, він встановив, що міцність найтонших кристалів скла має дорівнювати 11 ГПа, тобто близькою до теоретичної – 14 ГПа. Подібні результати, але вже на зразках монокристалів з кам’яної солі, були отримані А.Ф. Йоффе (1924 р.). Якщо у повітрі ці монокристали мали границю міцності 4,4 МПа, то вже у гарячій воді їх міцність зростала до 160 МПа. Ці експерименти показали, що внаслідок розчинення поверхні зразка зникають дефекти, які були на ній, тому міцність зразка різко зростає.

Чому ж поверхневі дефекти так впливають на міцність? Щоб зрозуміти це, скористаємось поняттям концентрації напружень, яке з’явилось напочатку XX ст.

Цікавою є історія відкриття цього явища. У 70-х роках XIX ст. на зміну парусному прийшов броненосний флот. Ведучі військово-морскі держави почали будувати гігантські кораблі – ескадронні броненосці, - водовиміщенням у 20000 тон і потужною бронею. Машини корабля використовували тони вугілля, масел, води, а ще службу ніс екіпаж, тобто люди, люди... Тому в корпусі корабля конструкторам доводилось залишати різного роду отвори: люки, ілюмінатори, місця для трубопрово­дів, бійниці орудий.

І раптом ці величезні кораблі, розраховані за усіма привилами науки, один за одним почали руйнуватися, причому руйнування відбувалось миттєво. Відбувалось це задовго до ката­строф із «Ліберті», задовго до Другої світової війни. Інженери-кораблебудівельники намагались врахувати вплив отворів у розрахунках і підсилювали краї отворів – адже напруже­ння це сила, поділена на площу перерізу, тобто при зменшенні перерізу за рахунок отвору напруження у ньому зростають обернено-пропорційно до площі ослабленого перерізу.

Пояснимо це на прикладі. Нехай суцільна пластина розтягується силами Р, які створюють напруження 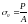, де А – площа перерізу пластини. Виріжемо у цій пластині отвір, який зменшить її переріз на 20% (рис. 1.4).

Тоді, згідно наших уявлень про напруження, на контурі отвору вони дорівнюють: .

Проте німецький механік Г. Кірш, теоретично визначивши у 1898 році напруження у точках А і В, виявив, що напруження там перевищують у 3 рази (а не у 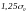) напруження у суцільній пластині.

Такий ефект і нази­вається концентрацією напружень, а число, яке показує, у скільки разів напруження біля отвору більше від номінального (тобто, у суцільній пластині), називається коефіцієнтом концентрації напру­жень К_1с. У нашому прикладі цей коефіцієнт дорівнює 3.

У випадку еліптичного отвору коефіцієнт концентрації напружень, визначений англійским корабельним інженером К.Інглісом, дорівнює 1+2(а/b), де а/b – відношення півосей еліпса (а>b).

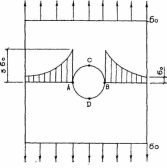
Рис. 1.4. Розтягування пластини з отвором

Саме концентрація напружень є причиною складного напруженого стану в бетоні при прикладанні зовнішнього навантаження. Напруження концентруються на твердіших частинках заповнювачів і у місцях, ослаблених порами. Подивимось, що відбувається у бетоні при дії стискувального навантаження: в околі тріщини створюються і стискувальні, і розтягувальні напруження.

Якщо уявити гелеві пори у вигяді кілець, тоді, дуже умовно, звичайно, схема напруженого стану стиснутого бетонного зразка буде мати вигляд, зображений на рис. 1.5 (знаком "-" традиційно позначають стиск, а "+" – розтяг). Розтягувальні напруження накладаються одне на одного, досягають величини R_bt. Це, звичайно, дуже спрощена схема руйнування бетону, - ніби перше наближення. Далі ми будемо знайомитись із механізмом руйнування бетону детальніше.

Але якщо до середини XX ст. уже все було відомо про концентрацію напружень, то чому раптом руйнувались американ­ські есмінці, адже тріщини зароджувались біля гострих кутів люків? Звичайно ж, концентрацію напружень враховували, а от структура металу для корпусів есмінців виявилась із дефектами – адже йшла війна. Навколо цих дефектів теж відбувається зміна напруженого стану, яка, накладаючись на поля напружень навколо кутів люків, призводить до пікових значень напружень і виникненню тріщин.

Тепер уявимо тріщини на поверхні кристалу кам’яної солі у досліді А. Йоффе у вигляді сильно витягнутих еліпсів. Приймемо співвідношення півосей еліпса а/b=25, тоді К_к=51. Поділивши міцність кристалу з гладкою поверхнею на К_к, отримаємо 2000/51=39,2 МПа, що приблизно відповідає технічній міцності кам’яної солі. Тобто досконалість структури кристалу призводить до підвищення міцності.

Крім того, статистичні теорії міцності теоретично підтвердили негативну роль дефектів у кристалах і встановили, що ймовірність появи у тілі небезпечного дефекту збільшується разом із збільшенням об’єму тіла (так званий масштабний ефект).

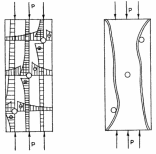
Рис. 1.5. Схема напруженого стану стиснутого призматичного зразка (а), схема руйнування бетонної призми (б)

Н а рис. 1.6 показана залежність міцності скляних волокон від їх діаметра . Графік одержано експериментальним шляхом, але він узгоджується із результатами статистичних теорій міцності. Наприклад, волокно кристалу заліза діаметром 1,6 мкм має міцність 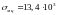МПа, що майже у сто разів більше від міцності монокристалів заліза для зразків звичайних розмірів.

Рис. 1.6. Залежність міцності скляних волокон від їх діаметра

Крім дефектів, що є результатом взаємодії дислокацій на рівні кристалічної решітки, в матеріалі можуть бути також і тріщини, походження яких пов’язано з передісторією цього матеріалу. Тріщини можуть виникати і в процесі його навантаження при експлуатації. Кожний вид таких дефектів по-своєму впливає на міцність матеріалів і є предметом досліджень механіки руйнування.

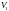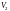Разом з тим, згаданий вище масштабний ефект свідчить про те, що великі тіла, як правило, мають меншу міцність, ніж малі тіла тієї самої форми. Вперше вплив об’єму зразків на границю міцності матеріалу описав шведський математик і механік В. Вейбул (1939 р.) за допомогою статистичного методу. Він показав, що для двох подібних зразків з одного матеріалу, але різного об’єму і , відношення середніх значень границь міцності будуть пов’язані залежністю

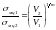, (1.13)

де - постійна матеріалу, що характеризує його неоднорідність та знаходиться із експерименту.

Формула (1.13) була підтверджена експериментально українським вченим М. Давиденковим (1947 р.) на циліндричних зразках із крихкої сталі. Так, для зразків з діаметрами 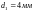та , довжинами 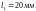та було знайдено, відповідно, границі міцності та 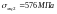. Параметр , визначений із формули (1.13), дорівнював .

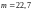Для цього ж матеріалу ( ) границя міцності зразка з 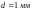та 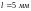за формулою (1.13) дорівнює . Експерименти дали значення 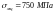. Похибка складає всього 4 %. Для інших матеріалів та видів навантаження параметра m може приймати інші значення. Наприклад, при визначенні границі втоми на згин двох зразків з діаметрами 10 мм і 100 мм виявилося, що для більшого зразка вона зменшилась на 40%, а стала . Для волокнистих композитних матеріалів параметр знаходиться в межах .

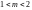Застосування статистичних методів у механіці крихкого руйнування розглядалось у працях А.М. Фрейденталя, а для оцінки міцності волокнистих композитів – у працях Ю.М. Работнова.