4.8. Розрахунок залізобетонних елементів за енергетичним критерієм
Розглянемо
залізобетонний елемент, до якого
прикладене зовнішнє навантаження у
вигляді сконцентрованої сили Р
(рис.
4.6). Робота
виконувана нею, чисельно рівна добутку
сили Р
на величину прогину f
(адже робота - це сила, помножена на
викликане нею переміщення у напрямку
дії сили).
Отже:
(4.49)
Робота,
виконувана зовнішніми силами, чисельно
дорівнює роботі внутрішніх сил
.
Щоб зруйнувати залізобетонний елемент,
потрібно виконати роботу для деструкції
розтягнутого бетону нормальним відривом,
стиснутого бетону – поперечним зсувом,
смуги бетону між тріщинами відриву та
зсуву – відривом і зсувом, поздовжньої
арматури відривом і поперечної –
зсувом, відігнутих стержнів – теж
відривом (оскільки похила тріщина
розвивається перпендикулярно до
відігнутого стержня).
Тоді робота внутрішніх сил:
(4.50)
Рис.
4.6. Залізобетонний згинальний елемент
у
граничному стані III
Порівнявши
праві частини (4.49) та (4.50), отримаємо
рівняння балансу роботи для згинального
залізобетонного елемента. Зауважимо,
що в цьому випадку нема однієї традиційно
невідомої у теорії опору залізобетону
величини - х.
Тому при вирішенні ординарних для
залізобетону задач (визначення несучої
здатності за відомим армуванням або
підбір розтягнутої арматури за
значенням
або
)
використовується одне-єдине рівняння.
А одне – це набагато менше, ніж два чи
три (на 100 чи навіть 200%).
4.9. Приклади розрахунку Приклад 1
Дано:
згинальний залізобетонний елемент
прямокутного перерізу b
= 0,3
м;
h
= 0,8
м; а
=
0,007 м, розтягнута арматура класу А400С,
(6
),
бетон В30, розрахунковий згинальний
момент М
540
кНм.
Необхідно перевірити максимальну несучу здатність перерізу (умову прикладу взято із «Руководства по проектированию бетонных и железобетонных конструкций из тяжелого бетона без предварительного напряжения», стор.45).
Розрахунок.
Згідно з табл. 4.1, для бетону класу В30
Попередньо визначаємо за формулою (4.5)
де
а за формулою (4.4)
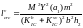
знаходимо довжину тріщини нормального відриву
коефіцієнт
m
при
цьому: m=(2
(2
,
оскільки діючий момент M
=
540 кНм = 0,54МНм > 0,4 МНм.
Довжину
тріщини поперечного зсуву визначаємо
за частково модифікованою формулою
(4.23); ми маємо право на такі зміни, оскільки
зерна крупного заповнювача є перешкодою
на шляху зсувних тріщин. Врахувавши
невеликі розміри балки, приймемо, що
вона виготовлена з бетону з максимальним
діаметром заповнювача 
тоді
Ширину розкриття тріщини поперечного зсуву розрахуємо за (4.31), врахувавши, що
де
0,007/0,8=0,00875.
Визначимо
висоту стиснутої частини перерізу
:
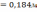
м.
і
приймаючи 
,
обчислимо максимальне значення несучої
здатності перерізу
тобто міцність перерізу забезпечена. У прикладі із «Руководства по проектированию бетонных и железобетонных конструкций из тяжелого бетона без предварительного напряжения» несуча здатність перерізу, розрахована згідно діючих норм, становить 585 кНм.