Тема 1.2 Математическая теория поля.

Скалярные поля. Графическое изображение скалярного поля. Поверхности одного уровня. Градиент скалярного поля.

Векторные поля и их графическое изображение. Векторные линии. Потенциальные поля. Поток вектора через поверхность. Теорема Гаусса. Дивергенция. Соленоидальные поля. Циркуляция векторного поля. Ротор. Теорема Стокса. Вихревые поля.

Оператор Гамильтона. Дифференциальные операции первого порядка. Действие оператора Гамильтона на произведения скалярных и векторных полей. Оператор Лапласа. Дифференциальные операции второго порядка. Гармонические поля.

Криволинейные ортогональные системы координат. Коэффициенты Ламе. Основные дифференциальные операции в криволинейных координатах.

Цилиндрические и сферические координаты. Запись основных дифференциальных операций в цилиндрических и сферических координатах.

Ключевые слова: математическое поле, скалярное поле, стационарное поле, нестационарное поле, эквипотенциальные поверхности, производная скалярного поля, градиент скалярного поля, векторное поле, векторные линии, поток векторного поля, дивергенция векторного поля, циркуляция векторного поля, ротор векторного поля, дифференциальные операции первого порядка, гамильтониан, дифференциальные операции второго порядка, лапласиан, потенциальное поле, вихревое поле, гармоническое поле, криволинейные координаты, базисные векторы, коэффициенты Ламэ, координатные линии, координатные поверхности, цилиндрическая система координат, сферическая система координат.

В математической физике понятие поле используется для обозначения совокупности значений некоторой физической величины, заданной в каждой точке пространства или его области. Если каждой точке пространства поставлено в соответствие определенное значение некоторой скалярной величины, то говорят, что в этом пространстве определено скалярное поле этой величины. Например, температура воздуха в разных точках пространства образует поле температур, атмосферное давление – поле давлений, а значение потенциала точечного заряда в разных точках пространства – поле электростатического потенциала.

Поскольку каждая точка поля определяется своими координатами , то задание скалярного поля эквивалентно заданию некоторой скалярной функции .

Скалярное поле вида называется стационарным, а скалярное поле вида – нестационарным.

Графически скалярное поле изображается с помощью эквипотенциальных поверхностей. Совокупность точек, в которых скалярное поле имеет одинаковое значение, называется поверхностью уровня или эквипотенциальной поверхностью. Уравнения эквипотенциальных поверхностей имеют вид:

,

Основной характеристикой скалярного поля является градиент. Градиентом скалярного поля называется вектор, направленный в данной точке по нормали к поверхности уровня в сторону возрастания скалярного поля и численно равный производной скалярного поля в точке по нормали:

.

Градиент скалярного поля обладает следующими свойствами:

1) градиент скалярного поля есть вектор , в направлении которого скорость изменения поля наибольшая, причем длина его

;

2) , где – постоянная;

3) , где ;

4) ;

5) ;

6) .

Если каждой точке пространства поставлено в соответствие определенное значение некоторой векторной величины, то говорят, что в этом пространстве определено векторное поле этой величины. Векторное поле можно рассматривать как вектор-функцию радиус-вектора точки или как вектор-функцию трех скалярных переменных :

.

Примером векторного поля является поле вектора , которое определено в каждой точке пространства, если известно скалярное поле .

Для графического изображения векторного поля вводят понятие векторной, или силовой, линии. Векторной линией векторного поля называется кривая, в каждой точке которой касательная совпадает с направлением поля в этой точке. Уравнения векторных линий векторного поля находят из системы дифференциальных уравнений

.

Потоком векторного поля через бесконечно малую площадку называется величина

,

где - значение векторного поля на площадке ; - проекция вектора на направление положительной нормали.

Поток векторного поля через замкнутую поверхность

.

Основными характеристиками векторного поля являются дивергенция и ротор. Дивергенцией векторного поля в данной точке называется предел, к которому стремится отношение потока векторного поля через произвольную, окружающую данную точку, поверхность к ограниченному этой поверхностью объему при стремлении последнего к нулю:

.

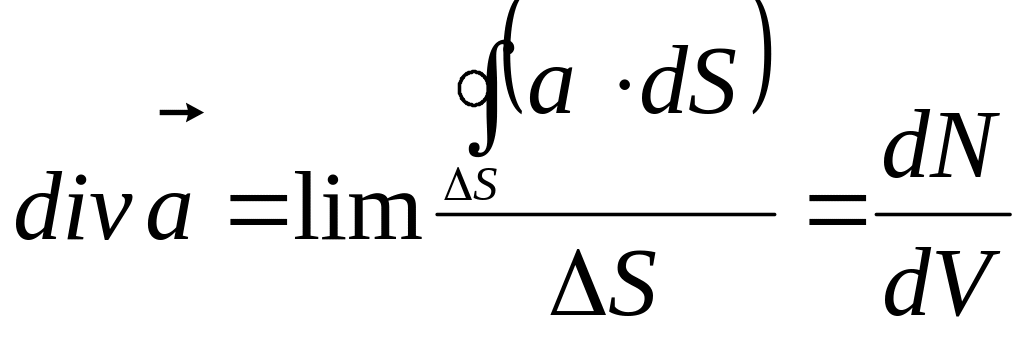Дивергенция векторного поля обладает следующими свойствами:

1. дивергенция векторного поля есть скалярная функция

;

2) , – постоянная;

3) ;

4) .

Точки векторного поля, для которых дивергенция положительна, называются источниками поля, а точки, для которых дивергенция отрицательна, – стоками. Численная величина дивергенции векторного поля называется мощностью или обильностью источников поля.

Векторное поле, для которого дивергенция равна нулю, называется соленоидальным.

Теорема Остроградского-Гаусса: поток векторного поля через произвольную замкнутую поверхность равен тройному интегралу от дивергенции, взятому по объему, ограниченному этой поверхностью:

.

Циркуляцией векторного поля вдоль кривой называется линейный интеграл

.

Ротором векторного поля в точке называется вектор, проекция которого на направление нормали равна пределу отношения циркуляции векторного поля по контуру плоской площадки , перпендикулярной в точке этому направлению , к площадке , когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:

.

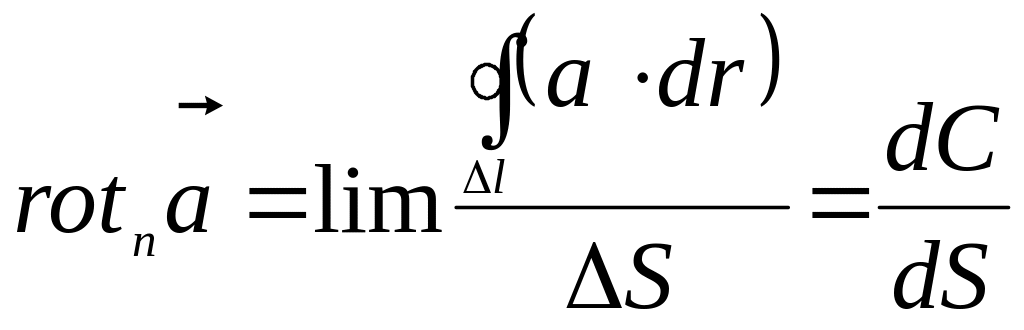Ротор векторного поля обладает следующими свойствами:

1. ротор векторного поля есть векторная функция

;

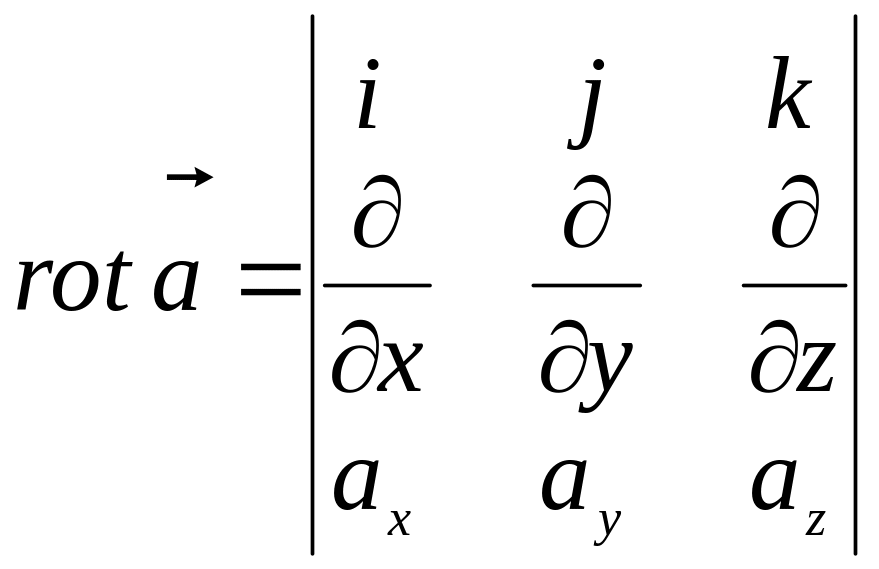2) , – постоянная;

3) ;

4) .

Ротор векторного поля характеризует вращательную способность векторного поля в данной точке.

Векторное поле, ротор которого равен нулю, называется потенциальным.

Теорема Стокса: циркуляция векторного поля по замкнутому контуру равна потоку ротора этого вектора через произвольную поверхность, опирающуюся на данный контур:

.

К основным дифференциальным операциям над скалярными и векторными полями относятся:

градиент скалярного поля (векторная величина)

;

дивергенция векторного поля

;

ротор векторного поля

.

Эти дифференциальные операции могут быть записаны с помощью символического дифференциального оператора, введенного ирландским математиком У.Р. Гамильтоном. Оператор Гамильтона обозначается символом (читается «набла»; набла – древний музыкальный инструмент треугольной формы) и в декартовой системе координат имеет вид

.

Рассмотрим действие дифференциального оператора на скалярную функцию и на векторную функцию . Результат такого действия являются следующие функции:

;

;

.

Рассмотрим действие оператора Гамильтона на произведения скалярных и векторных полей. В этом случае учитывают, что оператор Гамильтона представляет собой оператор дифференцирования и подчиняется правилу дифференцирования произведения. Результат действия оператора Гамильтона на произведения скалярных и векторных полей следующий:

;

;

.

Результат применения оператора Гамильтона к произведению двух векторных полей следующий:

;

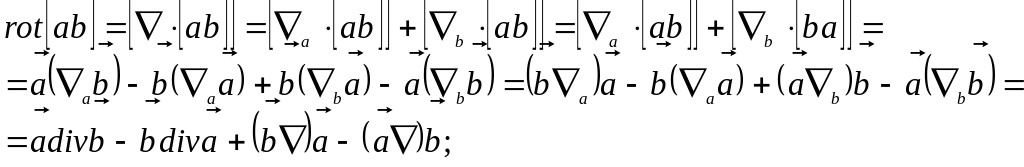
При решении конкретных задач для вычисления градиента скалярного поля, дивергенции и ротора векторного поля приходится пользоваться определенной системой координат. Иногда применение декартовых координат может оказаться неудобным. В таких случаях положение точки в пространстве определяется не тремя декартовыми координатами, а тройкой чисел , которые связаны с данной задачей более естественным образом. Например, для задач с осевой симметрией удобно пользоваться цилиндрическими координатами, а для задач с шаровой симметрией – сферическими координатами.

Числа , определяющие положение точки в пространстве, называются криволинейными координатами. Так как радиус-вектор некоторой точки однозначно определяется ее прямоугольными координатами, то криволинейные координаты являются функциями декартовых координат этой точки: , и обратно.

Уравнения определяют поверхности уровня для скалярных функций . Придавая константам различные значения, получаем три семейства поверхностей, которые называются координатными. Пересечение двух координатных поверхностей называется координатной линией. Вдоль каждой координатной линии изменяется только одна координата, а две другие остаются постоянными. Направления координатных линий задаются единичными базисными векторами (ортами) , которые в каждой точке пространства направлены по касательным и координатным линиям в сторону возрастания переменных .

Система криволинейных координат называется ортогональной, если ее базисные векторы удовлетворяют следующим соотношениям:

Величины называются коэффициентами Ламе данной ортогональной криволинейной системы координат. Элементы длин дуг соответствующих координатных линий, элементы площадей координатных поверхностей и элемент объема выражаются при помощи коэффициентов Ламе следующим образом:

,

, ,

.

Выражения для основных дифференциальных операций в криволинейных ортогональных координатах имеют вид:

;

;

.

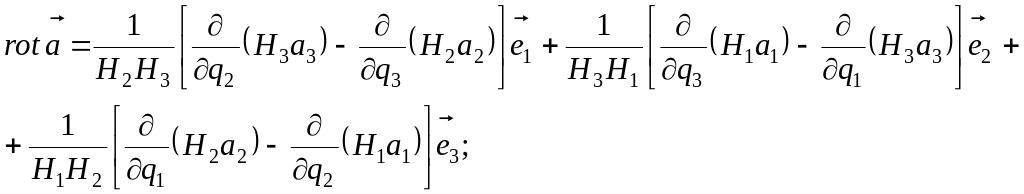
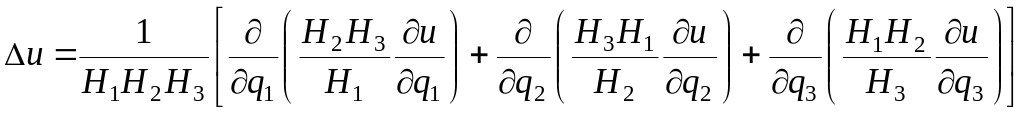При решении задач часто встречаются две системы криволинейных координат: цилиндрическая и сферическая. В цилиндрической системе координат положение точки пространства определяется тремя величинами: расстоянием от точки до фиксированной прямой ; углом , образованным фиксированной плоскостью и полуплоскостью, ограниченной осью и проходящей через фиксированную точку этой прямой. В цилиндрической системе координат , причем .

Координатными поверхностями в случае цилиндрической системы координат являются: – цилиндры с осью ;

– полуплоскости, ограниченные осью ; – плоскости, перпендикулярные к .

Координатными линиями будут: линии – лучи, перпендикулярные к оси с началом на этой оси; линии – окружности с центрами на оси и радиусами , плоскости которых перпендикулярны к этой оси; линии – прямые, параллельные оси .

Связь декартовых координат точки с ее цилиндрическими координатами выражается соотношениями . Коэффициенты Ламе в цилиндрической системе координат:

,

,

.

Элементы длин дуг соответствующих координатных линий, элементы площадей координатных поверхностей и элемент объема в цилиндрической системе координат с учетом коэффициентов Ламе выражаются формулами:

,

, ,

.

Для основных дифференциальных операций в цилиндрической системе координат получаются следующие выражения:

;

;

.

В сферической системе координат положение точки пространства определяется тремя величинами: расстоянием от точки до фиксированной точки ; углом , образованным радиус-вектором точки и фиксированной полупрямой ; углом , образованным фиксированной плоскостью и полуплоскостью, ограниченной осью и проходящей через точку . В сферической системе координат , причем .

Координатными поверхностями в случае сферической системы координат являются: – сферы с центрами в точке ; – конусы с осью ; – полуплоскости, ограниченные осью .

Координатными линиями будут: линии – лучи, выходящие из центра ; линии – окружности (меридианы) с центрами в точке и радиусами , пересекающие ось ; линии – окружности (параллели) с центрами на оси и радиусами .

Связь декартовых координат точки с ее сферическими координатами выражается соотношениями Коэффициенты Ламе в сферической системе координат:

,

.

Элементы длин дуг соответствующих координатных линий, элементы площадей координатных поверхностей и элемент объема в сферической системе координат с учетом коэффициентов Ламе выражаются формулами:

,

, ,

.

Для основных дифференциальных операций в сферической системе координат получаются следующие выражения:

;

;

.
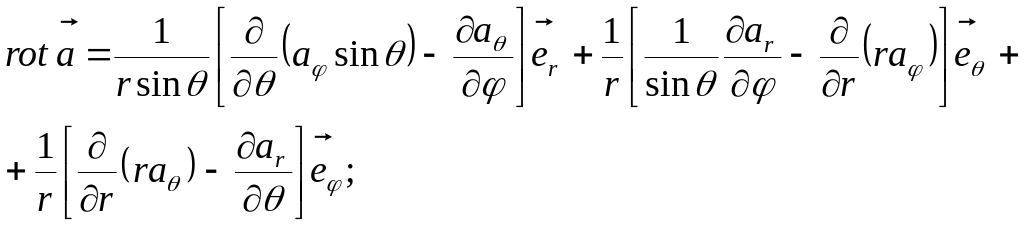