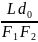Действительные и мнимые изображения.

Р ассмотрим светящиеся точки (точечные источники света), находящих­ся на конечном расстоянии от линзы. Будем всегда считать источники расположенными слева от линзы. Что касается изображений, то в зависимости от вида линзы и положения источника относительно нее изображение S' может находиться как справа, так и слева от линзы. Если изображение лежит справа от линзы, то это означает, что оно образовано сходящимся пучком лучей (рис. 201, а), т. е. лучей, которые действительно проходят через точку S'. Изображение в этом случае называется действительным. Оно может быть получено на экране, фотопластинке и т. п. Восстановив ход лучей, приведших к образованию изоб­ражения, мы можем всегда найти местоположение источника, хотя практически это обычно связано с не­которыми трудностями. Предположим теперь, что изображение лежит слева от линзы, т. е. с той же стороны от нее, как и источник. Это означает, что пучок лучей, расходящихся от источника, после преломления в линзе становится еще более расходя­щимся, и в точке S' пересекаются лишь воображаемые про­должения преломленных лучей (рис. 201, б). Изобра­жение в этом случае называется мнимым. В действитель­ности ничего «мнимого» в этом случае, конечно, нет. Осо­бенностью мнимых изображений является то, что их нельзя получить непосредственно на экране, фотопластинке и т. п.

Преломление света

1. Абсолютный показатель преломления среды: n₁ = 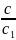, где c – скорость света в вакууме, c1 – скорость света в среде.

2. Если свет идет из среды с абсолютным показателем преломления n₁ в среду с абсолютным показателем преломления n₂, то

n = 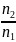= 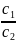- показатель преломления второй среды относительно первой.

3. Законы преломления:

1. Лучи, падающий и преломленный, и нормаль к границе раздела сред в точке падения лежат в одной плоскости.

2. Отношение синуса угла падения к синусу угла преломления равно относительному показателю преломления второй среды относительно первой: 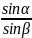= n = , где α – угол между падающим лучом и нормалью, β – угол между преломленным лучом и нормалью.

Ч ем больше показатель преломления, тем среда оптически более плотная. Если свет идет из менее плотной в более плотную оптически среду, то α>β, если, наоборот, из более плотной в менее плотную, то α<β. В последнем случае возможен случай, β = 90°, при котором sin α₀ = . При α>α₀ луч полностью отражается от границы раздела сред; такое явление называется полным внутренним отражением.

4. Сферическая поверхность, разделяющая две среды с показателями преломления n₁ и n₂, собирает узкий пучок лучей, идущий из точечного источника А₀ в первой среде, в точке А₁, являющейся изображением источника А₀ во второй среде. Формула такой оптической системы:

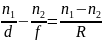
Обозначения понятны из рисунка. При этом d и f берутся со знаком «+» если точки А₀, А₁ – действительные, и со знаком «-» - если они мнимые; радиус R берется со знаком «+», если лучи, идущие от предмета, падают на выпуклую поверхность; со знаком «-» - если на вогнутую.

5. Л 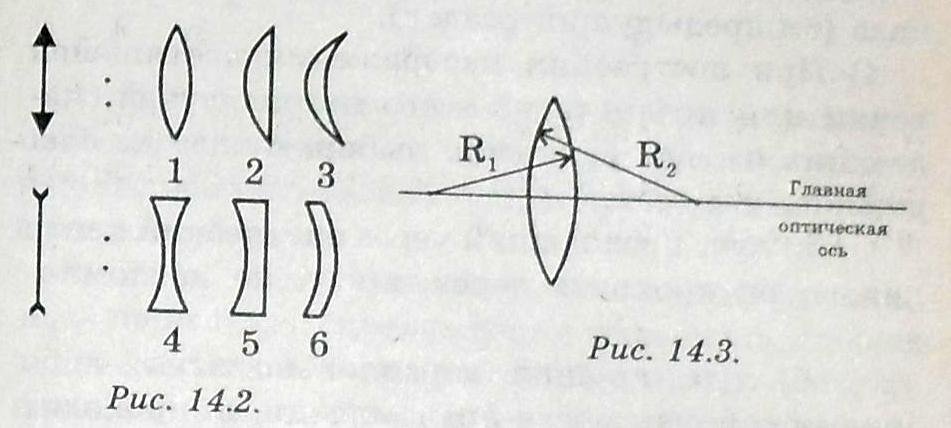инза есть прозрачное тело, ограниченное криволинейными поверхностями. Простейшие линзы – сферические.

6. Свойства тонких линз.

1. Параллельный пучок лучей после преломления в линзе собирается в одной точке, называемой фокусом (собирающие линзы). Геометрическое место фокусов есть плоскость, перпендикулярная оси линзы (фокальная плоскость) (рис. 14.4). Расстояние от фокальной плоскости до плоскости линзы есть фокусное расстояние F. Величина D = 1/F называется оптической силой линзы. Прямые, проходящие через оптический центр О линзы, называются оптическими осями.

2. Лучи, падающие на линзу параллельно какой-либо оптической оси, после преломления проходят через фокус, лежащий на этой оси.

3. Формула собирающей линзы: 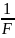= + 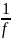, f – расстояние от оси линзы до ее фокуса,

4. При построении изображения светящейся точки или предмета из всего потока лучей, падающих на линзу, обычно выбирают два из следующих четырех:

А) луч, проходящий через оптический центр линзы; он проходит через линзу, не преломляясь;

Б ) луч, идущий параллельно какой-либо оптической оси; после преломления он проходит через фокус, лежащий на этой оптической оси;

В) луч, проходящий через передний фокус линзы, после преломления должен идти параллельно главной оптической оси;

Г) луч, проходящий через передний двойной фокус, после преломления пройдет через задний двойной фокус.

5. линейное увеличение предмета, даваемое собирающей линзой:

Г = = = 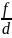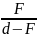, где H₀ - высота предмета, H – высота его изображения, d - расстояние от предмета до зеркала или линзы

7. Свойства тонких двояковыпуклых линз:

1. Параллельный пучок лучей после преломления в такой линзе расходится таким образом, что их продолжения пересекаются в одной точке – фокусе линзы. Геометрическое место фокусов есть плоскость, параллельная плоскости линзы. Все фокусы рассеивающей линзы мнимые.

2. Если лучи падают на такую линзу параллельно какой-либо оптической оси, то после преломления они выходят так, что их продолжения собираются в фокус, лежащий на этой оси.

3. Формулы рассеивающей линзы: - = ; Г = = =

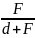
4. При построении изображений в рассеивающей линзе используют луч, идущий параллельно какой-либо оптической оси, и луч, идущий через оптический центр.

8. Если F - фокусное расстояние линзы, n_л – показатель преломления материала линзы, n _ср – показатель преломления среды, в которой находится линза, R₁ и R₂ – радиусы кривизны ограничивающих линзу поверхностей, то (*)

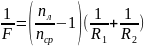Радиус кривизны выпуклой поверхности следует брать со знаком «+», вогнутой – со знаком «-», для плоской поверхности R = ∞.

9. Увеличение оптических приборов: Г = ,

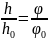где h, h₀ – линейные размеры изображения на сетчатке вооруженного прибором глаза и без него; φ, φ₀ – углы, под которыми глаз видит предмет через прибор и без него.

Увеличение, даваемое микроскопом: Г =

,где d – расстояние от предмета до объектива микроскопа; F₁ - фокусное расстояние объектива; F₂ – фокусное расстояние окуляра; d₀ – расстояние от мнимого изображения предмета до глаза наблюдателя. Расстояние L между окуляром и объективом (длина тубуса микроскопа):

L = +

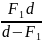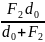
Если L, F₁ и F₂ известны, то (для нормального глаза) увеличение микроскопа: Г ≈