
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Кубанский Государственный Технологический Университет»
Кафедра информационных систем и программирования
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ УПРАВЛЕНИЯ
Часть 1
Методические указания к практическим занятиям по дисциплине «Информационные системы и технологии» для студентов всех форм обучения специальностей 230700.62 – «Прикладная информатика»
Краснодар 2013
УДК 681.31 (031)
Составители: Лойко В.И.
Кушнир Н.В.
Кушнир А.В.
Информационные технологии управления
Часть 1. Методические указания к практическим занятиям по дисциплине «Информационные системы и технологии» для студентов специальностей 230700.62 –Прикладная информатика – Краснодар: изд. КубГТУ, 2013. -24 с.
Приведены теоретические основы и задания к практическим занятиям по решению на ЭВМ задач одномерной оптимизации и управления запасами с использованием информационных технологий. Предназначены для студентов КубГТУ, изучающих курс " Информационные системы и технологии".
Библиогр.6 назв.
Рецензенты: д.т.н.,проф. Ключко В.И.
д.т.н., проф. Видовский Л.А.
Кубанский государственный технологический университет,
2013
Практическое занятие 1. Нахождение экстремума функции методом дихотомии
1.Цель и порядок выполнения работы
Цель работы - моделирование на ЭВМ одного из методов нахождения экстремума функции ( метода дихотомии ) и исследование на модели заданной функции.
Порядок выполнения работы:
ознакомиться с описанием работы;
разработать форму для приложения EXCEL, реализующие метод;
заполнить форму и отладить её;
исследовать заданную функцию;
оформить отчет.
2. Общие сведения
Суть метода дихотомии состоит в следующем. Если разделить заданный диапазон изменения функции, в котором отыскивается её экстремум, пополам, определить, в какой половинке находится экстремум, затем эту половинку поделить снова пополам, снова определить, в какой половинке находится экстремум и т.д., то в итоге этих повторяющихся действий мы попадем в точку экстремума. Но, очевидно, этот процесс деления бесконечен, так как точка по протяженности- бесконечно малая величина.
Следовательно, конечность вычислительного процесса по методу дихотомии может быть достигнута, если задастся допустимой погрешностью (Е ) вычисления координат точки экстремума. Поэтому в общем виде алгоритм нахождения экстремума функции сводится к следующему.
Пусть требуется найти максимум функции y =f(x ) в диапазоне изменения её аргумента от а до b с погрешностью +(-) Е по координате x (рис. 1.1).
Прежде всего следует проверить условие |b-a|<2 E. Если оно выполняется, то в пределах заданной погрешности мы уже находимся в "точки" экстремума. Если нет, то вычисляем две точки на оси x, находящиеся на расстоянии +E /2 от середины отрезка ab.
![]()
![]()
![]()
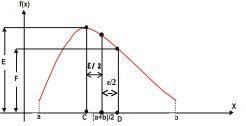
Рис. 1.1
Вычисление ординат этих точек необходимо для того, чтобы определить, в какой половине отрезка ab находится максимум функции.
Для этого вычисляем значения функции при x=C и x=D. Получим соответственно E=f(C) F=f(D).Теперь сравним значения E и F. Если E>F, то это значит, что максимум функции находится в левой половине отрезка ab, и мы "отбрасываем" правую половинку, т.е. "перемещаем" точку в точку D: b=D. Если условие не выполняется, то максимум находится в правой половине отрезка и производится перемещение точки а в точку C: а=C.
Далее перечисленные действия, начиная с проверки первого условия повторяются до тех пор, пока первое условие не будет выполнено. Это означает, что в пределах погрешности +E максимум достигнут. После чего производится выполнение функции в точке максимума
![]()
Для того, чтобы найти минимум функции, нужно условие E>F заменить условием F>E. Все остальные действия сохраняются.
3. Задание
3.1. Разработать метод в приложении EXCEL для нахождения max и min функции по методу дихотомии с допустимой погрешностью E =0,05.
Помимо определения координат экстремумов программа должна выводить на экран дисплея с заданным шагом таблицу значений функции и её график.
3.2. Варианты заданий
№ варианта |
Функция |
Диапазон изменения аргумента |
Шаг изменения аргумента |
1 |
y=2+Sinx |
0<x<2Pi |
x=0,5 |
2 |
y=2+Cosx |
-- |
-- |
3 |
y=1+Sinx |
-- |
-- |
4 |
y=1+Cosx |
-- |
-- |
5 |
y=10+5Sinx |
-- |
-- |
6 |
y=6+5Sinx |
-- |
-- |
7 |
y=7+5Sinx |
-- |
-- |
8 |
y=8+6Sinx |
-- |
-- |
9 |
y=7+4Sin |
-- |
-- |
10 |
y=21+19Sinx |
-- |
-- |
11 |
y=3+Cosx |
-- |
-- |
12 |
y=6+3Cosx |
-- |
-- |
13 |
y=x+Cosx |
-- |
-- |
14 |
y=2x+Cosx+1 |
-- |
-- |
15 |
y=0,5x+Cosx+1 |
-- |
-- |
16 |
y=2/x+2x |
0,1<x<2 |
x=0,2 |
17 |
y=1/x+x |
-- |
-- |
18 |
y=2/x+x |
-- |
-- |
19 |
y=2/3x+3x |
-- |
-- |
20 |
y=1/4+4x+1 |
-- |
-- |
21 |
y=1/x+5x |
-- |
-- |
22 |
y=1/x+1-e |
-- |
-- |
23 |
y=1/2x+3-e |
-- |
-- |
24 |
y=1/5x+x-1 |
-- |
-- |
25 |
y=1-e+1/x |
-- |
-- |
26 |
y=2-e+1/2x |
-- |
-- |
27 |
y=1/3x+x+2 |
-- |
-- |
28 |
y=0,1x-2x+10 |
0,1<x<2 |
x=0,2 |
29 |
y=1/5x+5x |
-- |
-- |
30 |
y=3/5x+8x |
-- |
-- |
4. Контрольные вопросы
4.1. В чем состоит идея метода дихотомии?
4.2. Какими свойствами должна обладать форма для EXCEL?
4.3. Что такое таблица значений функции?
4.4. Как создать график функции средствами EXCEL?
4.5. Объясните метод нахождения max и min функции методами EXCEL.
5. Содержание отчета
Практическое занятие 2. Моделирование основной задачи управления запасами ( модель Харриса )
