Вступ
Ефективна енергетика є важливою складовою рушійної сили економічного розвитку та технічного прогресу будь-якої держави. Кількісні і якісні енергетичні показники зростають у певній пропорції до збільшення населення: якщо за останні 100 років населення Землі збільшилось майже в 4 рази, то річне споживання енергетичних ресурсів виросло у 21 раз. Тому раціональне та економне використання всіх видів енергії є на часі актуальним як для всього людства, так і для України.
Протягом останніх років в енергетиці нашої держави нафта та природний газ складали більше 60 відсотків від всіх спожитих ресурсів. Наявний дефіцит в Україні цих цінних джерел енергії зумовлює гостру потребу в застосуванні більш ефективних, в плані перетворення хімічної енергії палив в теплову і далі в механічну енергію, теплових двигунів. До таких двигунів належать двигуни внутрішнього згоряння (ДВЗ), що використовуються в автомобільному, залізничному, річковому, морському і повітряному транспорті, в будівельних та сільськогосподарських машинах тощо.
Глибокі знання основних термодинамічних законів, процесів та циклів є фундаментом для розроблення високоефективних в термодинамічному розумінні ДВЗ, газотурбінних установок та турбореактивних двигунів.
1. Визначення характеристик робочого тіла
1.1 Робоче тіло – суміш ідеальних газів, масові частки яких: СО2=0,55; N2=0,05; O2=0,15; Н2О =0,25.
1.2 Молярні маси компонентів: μ1= 44,01 кг/кмоль; μ2= 28,013 кг/кмоль; μ3= 31,999 кг/кмоль; μ4= 18,02 кг/кмоль,
1.3 Питомі газові сталі компонентів:
,
(1.1)
де Rμ
– універсальна
газова стала,
;
μi – молярна маса і-го компонента.
,
,
,
.
.
1.4 Молярна маса суміші:
(1.2)
1.5 Об’ємні частки компонетів:
,
(1.3)
де gi – масова частка і-го компонента;
ri – обємна частка і-го компонента.
,
,
,
,
Перевірка
:
.
1.6 Питома газова стала суміші:
.
(1.4)
1.7 Густина та питомий об’єм суміші за нормальних умов:
(1.5)
(1.6)
1.8 Парціальні тиски компонентів суміші за нормальних умов:
,
(1.7)
де
– абсолютний тиск газової суміші, Па.
,
,
,
.
2. Розрахунок середніх теплоємностей суміші
2.1 Процес 1-2 – ізотерма
Попередньо визначаємо абсолютну температуру в точках 1 і 2.
Точка 1
(2.1)
.
(2.2)
Точка 2
(2.3)
.
(2.4)
2.2 Процес 2-3. Процес 2-3 є ізобарним (р= const).
Точка 3
(2.5)
.
(2.6)
.
(2.7)
2.3 Визначаємо теплоємність кожного компонента суміші в діапазоні температур від 0 до t2.
(2.8)
де
– коефіцієнти. Їхні значення в процесах
з сталим абсолютним тиском (p
= const)
для різних газів в ідеально-газовому
стані наведені в додатку Б
[1].
,
,
,
.
2.4 Tеплоємність кожного компонента суміші в діапазоні температур від 0 до t3.
,
,
,
.
2.5 Середня
теплоємність складових суміші в діапазоні
від
до
(від t2
до
t3)визначається
за такою формулою:
.
(2.9)
,
,
,
.
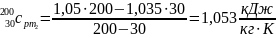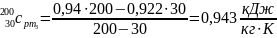2.6 Питома масова середня теплоємність суміші в діапазоні від t2 до t3.
,
(2.10)
.
2.7 Визначаємо ізохорну (v = const) теплоємності робочого тіла, використовуючи рівняння Маєра:
.
2.8 Процес 3-4 політропний (рvn = const).
Точка 4:
(2.11)
(2.12)
Визначаємо теплоємність кожного компонента суміші в діапазоні температур від 0 до t3.
,
,
,
.
2.9 Tеплоємність кожного компонента суміші в діапазоні температур від 0 до t4:
,
,
,
.
2.10 Середня теплоємність складових суміші в діапазоні від до визначається за такою формулою:
,
,
,
.
2.11 Питома масова середня теплоємність суміші в діапазоні від t3 до t4.
,
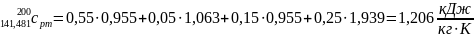2.12 Визначаємо ізохорну (v = const) теплоємності робочого тіла, використовуючи рівняння Маєра:
.
2.13 Уточняємо показник адіабати:
(2.13)
2.14 Визначаємо політропну теплоємності робочого тіла:
(2.14)
2.15 Процес 4-1 ізохорний (v= const).
Визначаємо теплоємність кожного компонента суміші в діапазоні температур від 0 до t1.
,
,
,
.
2.16 Tеплоємність кожного компонента суміші в діапазоні температур від 0 до t4:
,
,
,
.
2.17 Середня теплоємність складових суміші в діапазоні від до визначається за такою формулою:
,
,
,
.
2.18 Питома масова середня теплоємність суміші в діапазоні від t3 до t4.
,
2.19 Визначаємо ізохорну (v = const) теплоємності робочого тіла, використовуючи рівняння Маєра:
.
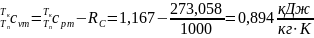