Приклад розв’язання завдання 3

Дано: у горизонтальному кожухотрубному конденсаторі суха насичена пара аміаку охолоджується водою, що рухається по трубах із зовнішнім діаметром d = 25 мм. Число рядів по вертикалі n = 7, розташування труб – шахове. Середня температура зовнішньої поверхні труб t_ст = 16,5°С. Тиск конденсації Р = 8,575 бар, що відповідає температурі насичення t_н = 20°С. Знайти середнє значення коефіцієнта тепловіддачі з боку сухої насиченої пари, що конденсується.

Рішення

Фізичні характеристики аміаку при t_н = 20°С (Додаток, табл. №7): теплота пароутворення r =1,19 МДж/кг, густина ρ = 610,3 кг/м³, коефіцієнт кінематичної в'язкості ν = 0,249·10^-6 м²/с, коефіцієнт теплопровідності λ = 0,494 Вт/(м∙К).

Приведена довжина визначається за формулою:

,

де g = 9,81 м/с² – прискорення вільного падіння, R = d/2 – зовнішній радіус труби. Підставляємо значення

.

Знаходимо допоміжний коефіцієнт

.

Коефіцієнт тепловіддачі для верхнього (першого) ряду труб:

Коефіцієнт, що враховує погіршення інтенсивності тепловіддачі на нижніх рядах труб пучка, обумовлене стіканням конденсату з верхніх рядів труб на нижні визначається по табл. 4 Додатку:

Середнє значення коефіцієнта тепловіддачі для першого ряду труб:

4. Теплопередача через плоску стінку

Теоретичні відомості

Теплообмін – процес передачі теплоти в середовищі з неоднорідним розподілом температури. Існує три механізми теплообміну: теплопровідність, конвекція та випромінювання.

Закон Фур’є: густина теплового потоку пропорційна градієнту температури

де λ – коефіцієнт теплопровідності, який характеризує індивідуальні фізичні властивості речовини. Знак ˝–˝ показує, що теплота поширюється по напряму зменшення температури.

В газах перенос теплоти здійснюється за рахунок переміщення молекул із холодної області в гарячу. Для газів величина коефіцієнту

Найбільше значення λ мають гелій і водень завдяки малій вазі і дуже високій рухливості.

В рідинах кожна молекула коливається довкола положення рівноваги, стикаючись з сусідніми молекулами. Теплота передається шляхом поширення цих коливань. Для рідин величина коефіцієнту

В металах носіями теплоти є вільні електрони, тому значення коефіцієнту λ досягають великих значень, особливо для чистих металів

В діелектриках, які використовуються в будівництві, коефіцієнт λ залежить від їх вологості та пористості і може приймати значення

Теплоізоляційні – матеріали з низьким значенням коефіцієнту теплопровідності (λ < 0,25 Вт/(м·К)). Коефіцієнт теплопровідності залежить від температури, його визначають експериментальним шляхом.

Теплопередача – теплообмін між двома теплоносіями через тверду стінку, що їх розділяє.

Тепловіддача – теплообмін між рідиною і поверхнею твердої стінки, яку рідина омиває. Щільність теплового потоку при тепловіддачі визначається по закону Ньютона-Ріхмана

де α – коефіцієнт тепловіддачі. Він дорівнює кількості теплоти, що переноситься в одиницю часу через одиницю поверхні стінки при різниці температур в 1 К між рідиною і поверхнею стінки.

Розглянемо випадок теплопередачі через плоску стінку (рис. 5).

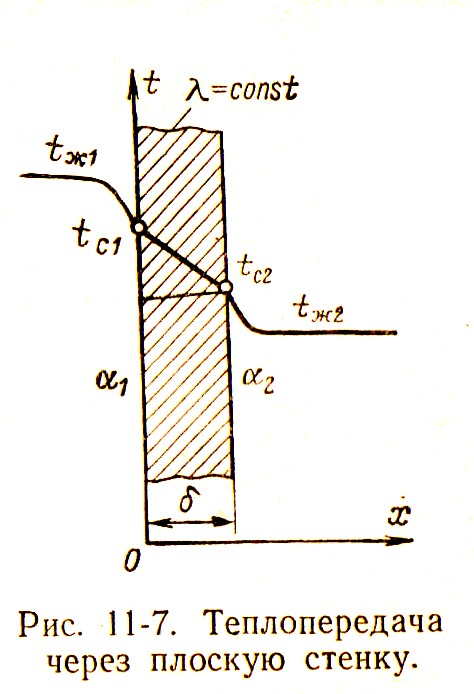
При стаціонарному режими щільність теплового потоку

Щільність теплового потоку, що передається від рідини 1 зовнішній поверхні стінки

Рис.5 Теплопередача крізь плоску стінку.

Щільність теплового потоку, що передається від зовнішньої до внутрішньої поверхні стінки

Щільність теплового потоку, що передається від внутрішньої поверхні стінки рідині 2

Склавши всі три вирази отримуємо для щільності теплового потоку

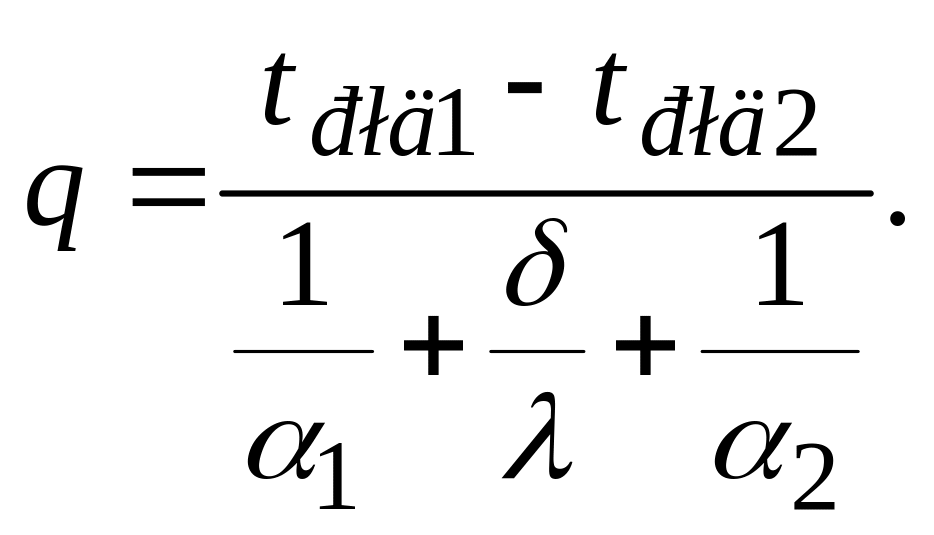
Коефіцієнт теплопередачі – щільність теплового потоку при різниці температур теплоносіїв в 1 К

Термічний опір теплопередачі – сума термічних опорів теплопередачі і термічного опору теплопровідності