3. Итерационные методы решения инженерных задач

3.1. Метод простой итерации. Суть метода. Последовательность операций

Впервые метод последовательных приближений был, по-видимому, использован для расчета балки переменного сечения в работе В.П. Ветчинкина [7], вышедшей в свет в 1926 году. В этой книге рассматривался вопрос о деформациях лопасти воздушного винта с учетом разгрузки ее центробежными силами, а также приводилось решение системы двух уравнений изгиба лопасти методом итераций без доказательства сходимости процесса. Книга В.П. Ветчинкина положила начало ряду исследований, основанных на применении итерационных методов.

В дальнейшем следует отметить работу Д.Ю. Панова [30], вышедшую в 1937 году. Д.Ю. Пановым были рассмотрены три итерационных метода расчета балки переменного сечения с учетом взаимного влияния деформаций изгиба и кручения: метод простой итерации, метод итерации в группах и смешанный метод, при котором первое приближение выполняется по методу итерации в группах, а последующие – простой итерации. Д.Ю. Панов рассматривал также вопрос о сходимости метода последовательных приближений в применении к уравнению изгиба балки длиной L переменного сечения с изгибной жесткостью B(x) с учетом осевой силы и привел доказательство этого метода для достаточно малых значений величины осевой силы .

Применение итерационных методов к решению прикладных задач теории упругости явилось предметом исследований В.В. Новожилова [27], И.В. Свирcкого [33] и ряда других авторов.

Обычный метод последовательных приближений строится по следующей схеме.

Пусть дано линейное дифференциальное уравнение с переменными коэффициентами –

(3.1)

где произвольный параметр. После двукратного интегрирования получим –

, (3.2)

где и константы интегрирования, определяемые краевыми условиями.

Обозначим

.

Подставляя под знаком интеграла уравнения (3.1) вместо его величину –

,

получим

.

Действуя аналогично, придем к соотношениям –

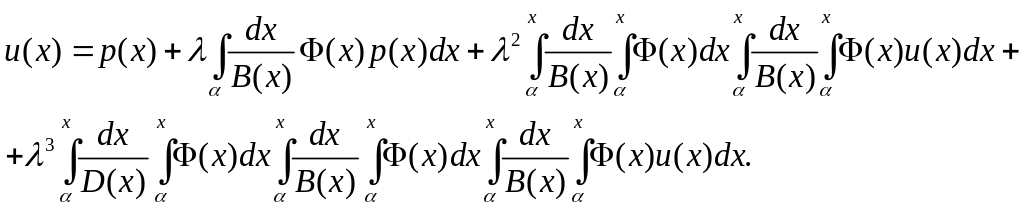(3.3)

Условимся обозначать

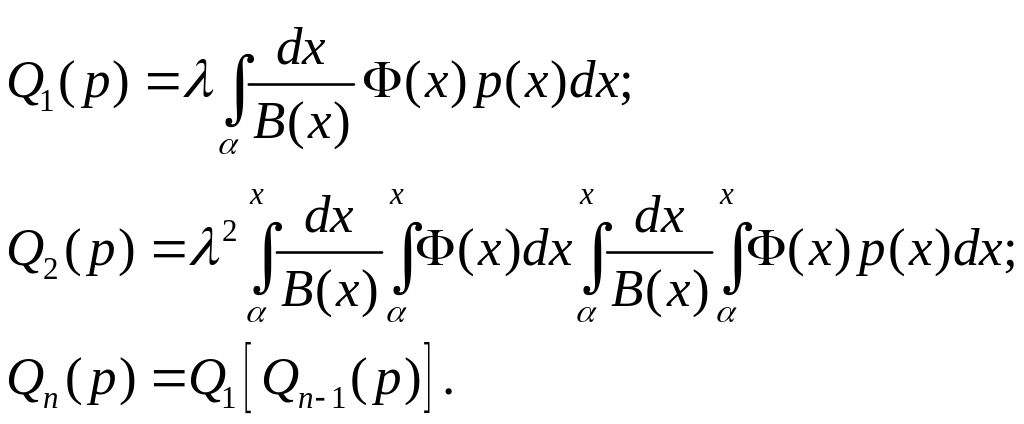(3.4)

В этих обозначениях уравнение (3.3) запишется следующим образом –

. (3.5)

Таким образом, если при неопределенном возрастании для всякого значения , лежащего на рассматриваемом интервале

(3. 6)

то решение и(х) уравнения (3.1) представляется рядом, каждый член которого получается из предыдущего интегральными операциями (3.4) –

(3. 7)

3.2. Сходимость итерационных методов

При решении вопроса о сходимости метода положим, что

(3.8)

тогда

.

Для выполнения условия (3.8) необходимо, чтобы интеграл от и(х) на рассматриваемом интервале был ограничен, т.е.

,

и соблюдалось неравенство

или . (3.9)

При этих условиях

(3.10)

Неравенства (3.8) и (3.9) обеспечивают также сходимость ряда (3.7) для и. Действительно, этот ряд допускает мажоранту представляющую собой сумму членов геометрической прогрессии со знаменателем Следовательно, ряд сходится при выполнении условия (3.10).

Если дополнительно наложить требования, чтобы при коэффициенты уравнения подчинялись условиям < ; < , то можно утверждать, что на рассматриваемом интервале ряд (3.7) сходится равномерно.

Однако условие (3.9) существенно ограничивает применение итерационных методов для решения краевых задач. В теории интегральных уравнений доказывается, что предельным значением радиуса сходимости итерационного метода по параметру является первое собственное значение уравнения, т.е. неравенству (3.9) эквивалентно неравенство

. (3.11)

В расчетной практике встречаются случаи, когда указанный диапазон сходимости по оказывается недостаточным.

В качестве примера можно привести задачу об изгибе распределенной нагрузкой вращающейся лопасти, которая описывается уравнением (3.1).

В этом случае коэффициенты уравнений имеют следующий физический смысл: изгибная жесткость в сечении с координатой х по длине лопасти, , где погонная масса.

Параметр равен квадрату угловой скорости вращения. Для рассматриваемой задачи неравенство (3.8) ограничивает применение метода итераций сравнительно малыми угловыми скоростями вращения лопасти.