1.3. Общая характеристика и уравнения задач теплопроводности

Исходные понятия и дифференциальное уравнение теплопроводности. Перенос тепла теплопроводностью в каком-либо теле в зависимости от условий имеет различный характер. Если тепло распространяется так, что температура в отдельных местах тела сохраняется неизменной во времени, то процесс переноса тепла носит стационарный характер. Если температура в этих местах тела меняется со временем, то такой не установившийся во времени процесс переноса тепла называется нестационарным. Тело, внезапно подвергаемое какому-либо достаточно длительному тепловому воздействию, постепенно теряет особенности своего начального теплового режима, и по прошествии некоторого времени нестационарный тепловой режим тела находится в полном подчинении примененного теплового воздействия. Такой нестационарный тепловой режим тела называют регулярным. В некоторых случаях тело подвергается периодическому тепловому воздействию, и температура в отдельных местах тела периодически меняется во времени, совершая простые или сложные колебания. При этих условиях перенос тепла в теле носит волнообразный характер.

Тело может подвергаться тому или иному стационарному или нестационарному тепловому воздействию как от поверхностей, ограничивающих объем тела, так и от внутренних источников тепла, действующих в самом теле. В последних случаях перенос тепла в теле называется теплопроводностью с источниками.

При решении задач теплопроводности приходится встречаться со всеми указанными особенностями теплового режима тел (различных по форме и содержащемуся веществу в объеме). Основной величиной для определения переноса тепла теплопроводностью в теле служит удельный тепловой поток, который определяется формулой –

, (1.24)

где коэффициент теплопроводности тела или среды; градиент температуры.

Решение задачи теории теплопроводности в общем случае сводится к нахождению распределения температур в теле в виде функции –

Здесь τ – время.

Для определения температурного поля тела в процессах распространения тепла теплопроводностью пользуются понятием изотермических поверхностей. В теле, в котором осуществляется перенос тепла, в любой момент времени можно выделить слои, ограниченные поверхностями с одинаковой температурой и одинаковым перепадом температур на поверхностях соответствующих слоев . Совокупность таких изотермических поверхностей в теле в любой момент времени представляет его температурное поле. При нагревании или охлаждении тела температура в отдельных местах его меняется со временем. Следовательно, в каждый последующий момент времени месторасположение изотермических поверхностей в теле также изменяется. Температурное поле в этих случаях будет переменным во времени или нестационарным. Неизменное во времени температурное поле отвечает стационарному тепловому режиму.

Вдоль изотермических линий тепло в теле распространяться не может, и перенос тепла осуществляется лишь в направлениях от одной изотермической поверхности к другой в сторону понижения температуры. Кратчайший путь распространения тепла в изотропном теле в любом месте, очевидно, соответствует направлению нормали к изотермической поверхности. Удельный тепловой поток в этом месте тела определяется формулой –

(1.25)

где градиент температуры по направлению нормали к изотермической поверхности.

Огибающие нормалей к изотермическим поверхностям на пути переноса тепла при последовательном переходе от одной изотермической поверхности к другой представляют собой линии теплового тока. Совокупность таких линий тока в теле представляет тепловой поток.

Баланс тепла в единичном объеме тела или среды при распространении тепла теплопроводностью приводит к следующему дифференциальному уравнению –

(1.26)

где и с_р — плотность и изобарная теплоемкость вещества тела, вектор переноса тепла теплопроводностью. Уравнение это представляет равенство, первый член которого представляет собой изменение энтальпии вещества в единичном объеме в единицу времени, второй член суммы есть результирующий перенос тепла теплопроводностью в единичном объеме в единицу времени. Правая часть уравнения – это удельная производительность источников тепла в единичном объеме.

В форме изменения температур уравнение теплопроводности представится в виде –

(1.27)

где коэффициент переноса тепла или теплопроводность тела.

Эта форма дифференциального уравнения теплопроводности представляет математическое описание процесса изменения температуры во времени в любом месте тела, вызываемое результирующим переносом тепла и действующими источниками энергии. Величина 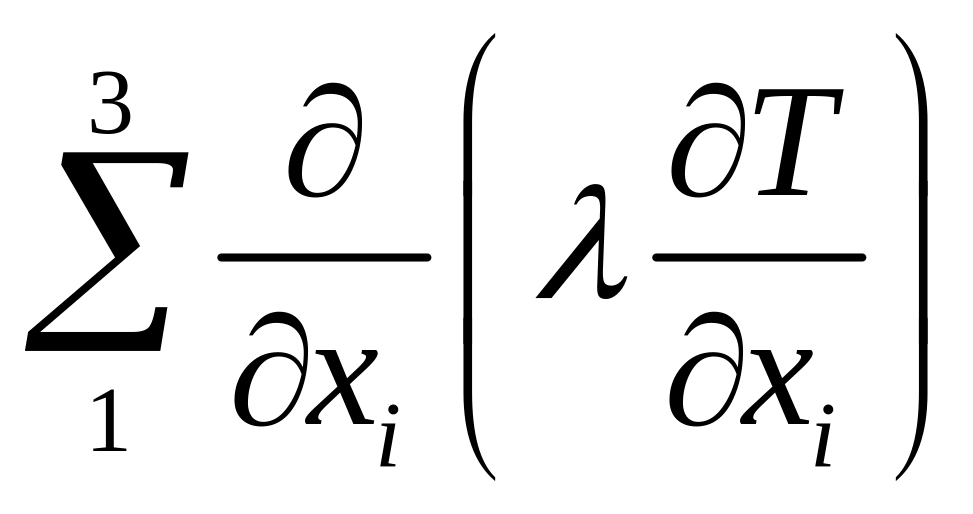представляет собой изменение энтальпии в единицу времени в любом месте тела от результирующего переноса тепла теплопроводностью в этом месте.

При отсутствии действующих источников тепла в теле дифференциальное уравнение теплопроводности запишется в виде –

(1.29)

Если температуропроводность тела сохраняется постоянной, то уравнение теплопроводности можно записать как –

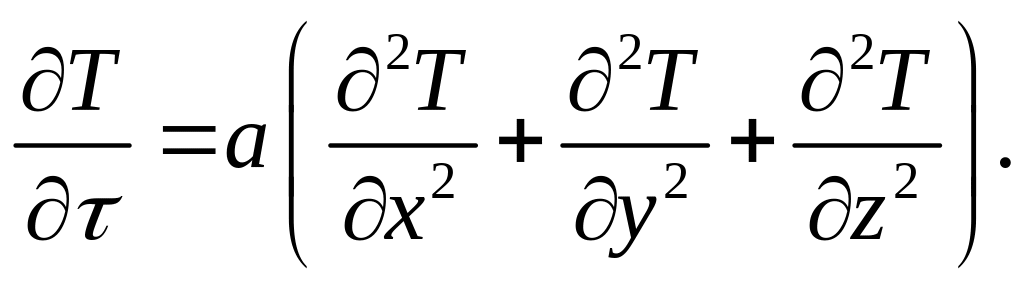
Или –

где Δ – дифференциальный оператор Лапласа.

Параметр имеет определенный физический смысл. Положительная или отрицательная его величина отвечает нагреванию ( >0) или охлаждению ( <0) тела в любом месте. Нулевое значение оператора соответствует стационарному тепловому режиму; в этом случае распределение температур в теле сохраняется неизменным во времени.

Дифференциальное уравнение –

(1.30)

соответствует стационарной теплопроводности тела. Интегрированием этого уравнения находят функцию распределения температур, представляющую стационарное температурное поле в теле.

Начальные и граничные условия задач теплопроводности. В практических приложениях теории теплопроводности приходится встречаться с различными задачами. Условно эти задачи можно разделить на следующие три группы:

1) стационарная теплопроводность тел;

2) нестационарная теплопроводность тел;

3) температурные или тепловые волны.

Решение всех этих задач требует интегрирования дифференциального уравнения теплопроводности, которое описывает любые случаи распространения тепла. Для нахождения распределения температур в теле для конкретных условий распространения тепла требуется привлечь известные краевые условия.

К краевым условиям относятся:

а) начальное распределение температур в теле, т. е. распределение температур до момента теплового воздействия на тело;

б) граничное условие теплового воздействия на тело.

Начальное распределение температур в теле может быть разнообразным. Наиболее простой случай соответствует одинаковой температуре массы тела во всем объеме –

. (1.31)

Такое условие может соответствовать, например, начальному тепловому состоянию тел перед их разогревом в печах или охлаждением в холодильниках.

Для решения задач теплопроводности должна быть известна начальная температурная функция тела .

Граничное условие теплового воздействия на тело может быть также разнообразным. Обычно различают три рода граничных условий:

1) на поверхности тела поддерживается заданное распределение температур;

2) на поверхности тела поддерживается заданное распределение удельных тепловых потоков;

3) поверхность тела окружает среда с заданной температурой и коэффициентом теплоотдачи.

Кроме трех граничных условий теплового воздействия на тело, в современных задачах теплопроводности приходится встречаться и с другими граничными условиями:

4) поверхность тела подвергается тепловому воздействию контактной теплопроводности другого тела;

5) при тепловом воздействии на поверхность тела осуществляется превращение его массы, а местоположение поверхности перемещается во времени. Последний случай граничного условия отвечает так называемым фронтовым процессам теплопроводности с превращением массы тела (плавление, затвердевание, выгорание, сублимация и т. д.).

В общем случае граничное условие теплового воздействия на тело можно записать следующим равенством –

,

где и представляют удельные тепловые потоки на границе тела в направлении нормали к поверхности с наружной (+n) и внутренней (–п) стороны; удельный поток превращаемой массы тела; скорость перемещения фронта превращения; плотность превращаемой массы тела; энергия превращения единичной массы тела. При отсутствии превращения массы тела поверхность теплового воздействия сохраняется неизменной во времени, и граничное условие определяется равенством –

.

Для граничного условия контактной теплопроводности это равенство запишется в виде

Применительно к граничному условию третьего рода для удельного теплового потока на поверхности тела можно записать следующие две формулы:

а) для переноса тепла на границе тела со средой

(1.32)

где коэффициент теплоотдачи в среде, и температуры тела на поверхности и окружающей среды;

б) для переноса тепла в массе тела на границе

где коэффициент теплопроводности тела, проекция градиента температуры на направление нормали к поверхности тела в момент времени .

Из формул для составляется выражение граничного условия третьего рода

где соответствующие разности переменной температуры тела и постоянной температуры окружающей среды .

Это уравнение связывает распределение температур в массе тела с граничным условием теплового воздействия на его поверхность для любого момента времени. Такое граничное условие теплового воздействия на тело в задачах теплопроводности и теплопередачи тел встречается наиболее часто.

Интегрирование линейного дифференциального уравнения второго порядка в частных производных представляет одну из классических задач математической физики. Эта задача успешно решается для граничных условий, соответствующих теплопроводности и теплопередаче плоской стенки, стенок труб, сферических слоев, стержня и др. Вместе с тем, при граничных условиях, соответствующих телам более сложной геометрии, решение этой задачи вызывает значительные сложности и может быть получено только приближенными методами.