7. Метод трефтца

Если в методах Ритца и Бубнова-Галеркина искомые функции должны обязательно удовлетворять граничным условиям, но не дифференциальным уравнениям задачи, то в методе Трефтца приближенное решение точно удовлетворяет дифференциальным уравнениям, но не удовлетворяет, вообще говоря, граничным условиям рассматриваемой задачи. Другими словами, в методе Трефтца применительно к задачам теории упругости функции в выражении (6.5) выбираются так, чтобы они были частными интегралами дифференциальных уравнений равновесия (6.4) задачи.

Как известно, вариационное уравнение Лагранжа (5.2) заключает в себе как уравнения равновесия, так и граничные условия. Если функции выбраны в соответствии с рекомендациями метода Трефтца, то в вариационном уравнении Лагранжа члены, содержащие уравнения равновесия, тождественно обратятся в нуль, и оно примет вид –

Подставляя сюда выражения (6.5), записанные для вариаций перемещений, и приравнивая к нулю множители перед независимыми вариациями δа_к, δb_к, δс_к, получим следующую систему –

Здесь правые части по-прежнему известны, а левые представляют собой линейные однородные (относительно коэффициентов а_к, b_к, с_к) выражения. Опять получена система линейных алгебраических уравнений, из которой находятся коэффициенты а_к, b_к, с_к.

Построив соответствующие минимизирующие последовательности, доказывают их сходимость к точному решению задачи. Тем самым метод Трефтца оказывается еще одним прямым приближенным методом решения краевых задач.

Заметим, что в отличие от методов Ритца и Бубнова-Галеркина этот метод позволяет оценивать значение энергетического интеграла (функционала) снизу. Тем самым при использовании метода Трефтца можно получить оценки снизу значений собственных частот колебаний, критических нагрузок и других параметров.

8. Примеры использования методов Ритца и Бубнова-ГалЕркина

Пример 1. Определение критической силы для консольного стержня со ступенчатым изменением жесткости (рис. 8.1).

При потере устойчивости деформированное состояние стержня описывается функцией прогиба , которую приближенно можно аппроксимировать конечной суммой –

Очевидно, что при этом удовлетворяются только кинематические граничные условия, поэтому рассматриваемую задачу будем решать методом Ритца.

Для изогнутого стержня работа внешней сжимающей силы –

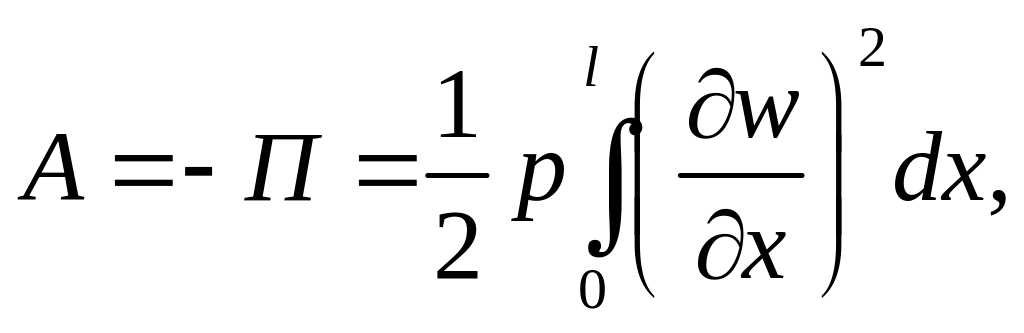
а потенциальная энергия деформации стержня составляет

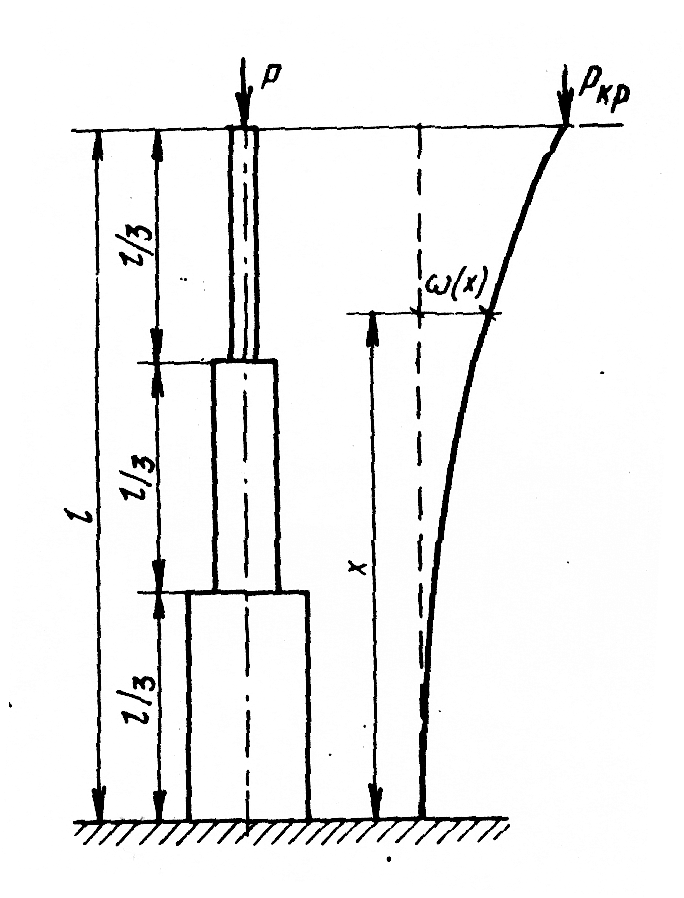
Рис. 8.1. Устойчивость консольного стержня

.

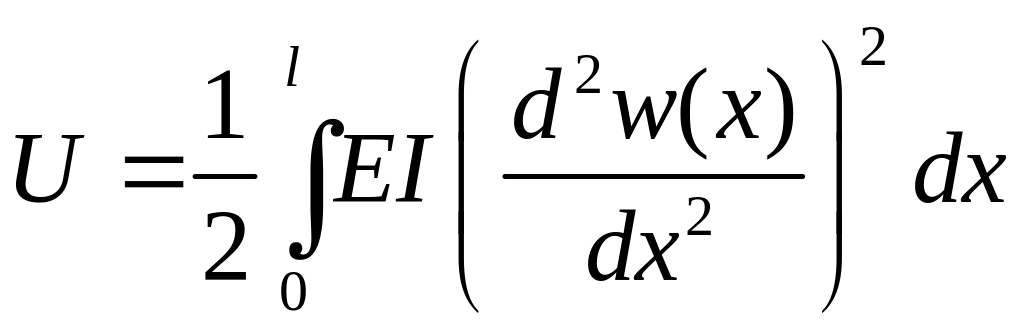Таким образом, выражение для полной потенциальной энергии системы приобретает следующий вид –

.

Подставляя сюда , получим приближенное значение энергетического интеграла –

.

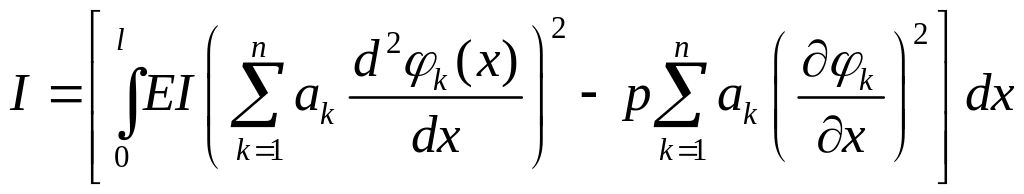Взяв в соответствии с процедурой метода Ритца, производные от по , запишем систему алгебраических уравнений –

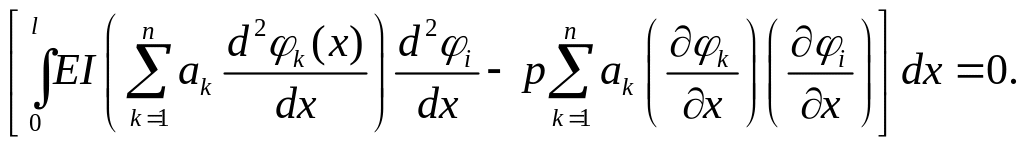
В первом приближении и

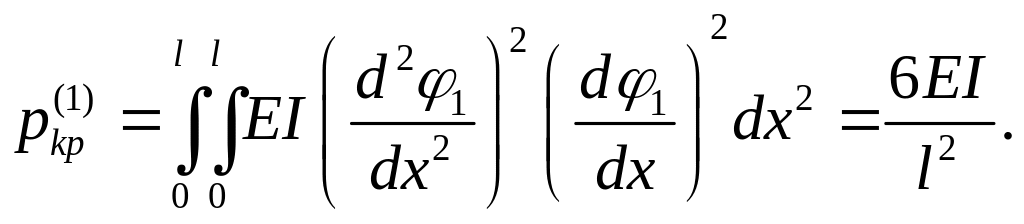
Во втором приближении и решение системы двух алгебраических уравнений дает значение критической силы

Третье приближение практически совпадает со вторым, поэтому найденное значение можно считать окончательным.

Пример 2. Определение первой частоты свободных колебаний консольной балки в виде треугольного клина (рис. 8.2).

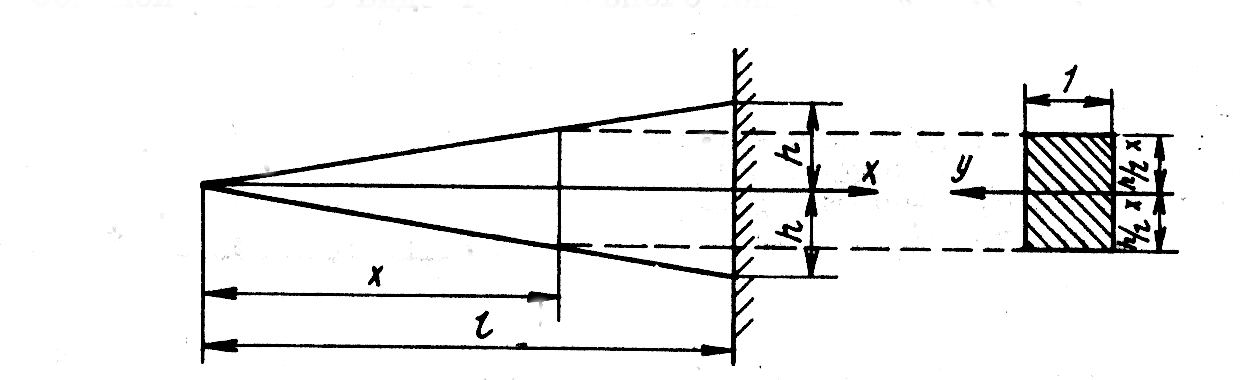
Рис. 8.2. Расчетная схема для определения первой частоты свободных колебаний консольной балки в виде треугольного клина

Геометрические характеристики балки переменной жесткости представляются следующими соотношениями –

Граничные условия – при х = 0 (на конце консоли) отсутствуют изгибающий момент и перерезывающая сила: а при x = l (в защемлении) прогиб и угол поворота сечения равны нулю: .

Выбираем функцию так, чтобы удовлетворялись граничные условия при

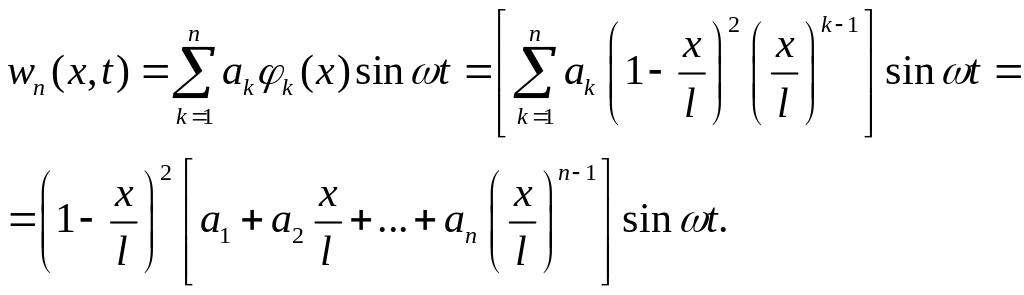
Дифференциальное уравнение колебаний стержня имеет вид –

откуда методом разделения переменных можно получить уравнение для форм свободных колебаний

.

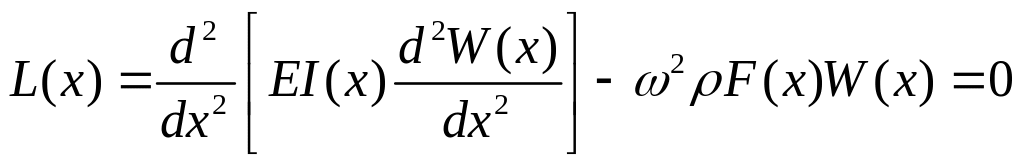В результате подстановки в это уравнение выражения для выбранного вида приближенного решения и выполнения требований ортогональности оператора к системе функций можно получить –

.

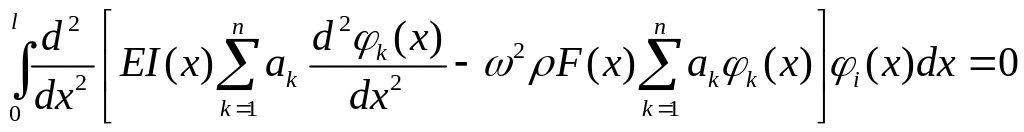В первом приближении (при удержании лишь одного члена суммы выражения для ) частотное уравнение имеет вид –

,

что дает _. Во втором приближении частотное уравнение находится из системы двух алгебраических уравнений, решенных относительно коэффициентов . Его решение позволяет найти частоту –

Интересно, что для этой задачи известно точное решение в функциях Бесселя, согласно которому , т.е. отличие второго приближения от точного решения составляет менее 0,1%.