5.3. Вариационные уравнения термоупругости

Когда упругое тело находится в условиях силового и теплового нагружения, удельная потенциальная энергия упругой деформации теряет свои потенциальные свойства. Если состояние тела описывается параметрами состояния или , то потенциалами будут соответственно удельная свободная энергия (плотность свободной энергии) и плотность термодинамического потенциала Гиббса . Здесь Т - абсолютная температура; =1, 2, 3.

Таким образом, при решении статической несвязанной задачи термоупругости в перемещениях следует исходить из обобщенного вариационного уравнения Лагранжа.

При решении статической несвязанной задачи термоупругости в напряжениях при фиксированных объемных силах необходимо обращаться к обобщенному вариационному уравнению Кастильяно –

.

В случае малых деформаций и небольшом отклонении текущей температуры Т от начальной Т_о плотности свободной энергии и термодинамического потенциала Гиббса определяются следующими выражениями.

Для изотропного материала –

где коэффициенты Ламе; коэффициент Пуассона; удельная теплоемкость при постоянной деформации; коэффициент линейного расширения; плотности энтропии, свободной энергии и термодинамического потенциала Гиббса соответственно; в начальном состоянии

Для анизотропного материала –

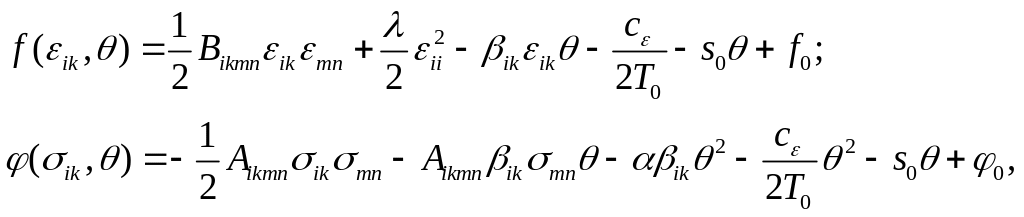
где компоненты тензоров коэффициентов Ламе и модулей упругости соответственно; компоненты тензора коэффициентов линейного расширения; компоненты тензора термических коэффициентов.

В случае малых деформаций изотропного тела при произвольном отклонении текущей температуры от начального значения выражения для плотностей свободной энергии и термодинамического потенциала Гиббса имеют вид –

где (Т)- истинный коэффициент линейного расширения материала.

Био в работе [19] обобщил вариационное уравнение Лагранжа на случай связанной задачи термоупругости при малом отклонении текущей температуры от начального значения. Соответствующее вариационное уравнение записывается следующим образом –

где для изотропного материала термоупругий потенциал; функция диссипаций; векторная функция, определенная соотношениями и ; плотность энтропии; компоненты вектора потока тепла; коэффициент теплопроводности; компоненты вектора внутренней нормали к поверхности тела.

Для анизотропного материала

где компоненты тензора термического сопротивления.

В работе Л.И. Балабуха и Л.А. Шаповалова [2] для изотропного тела при малых отклонениях температуры от начального значения дано обобщение вариационного уравнения Био, но при наличии тепловых источников и стоков, что в случае статической задачи сводится к добавлению в выражение термоупругого потенциала слагаемого где мощность внутреннего источника (стока) тепла.

Исследования в области вариационных принципов термоупругости продолжаются. К их числу относятся работы Э.И. Григолюка с соавторами [12]. В ряде работ рассмотрены экстремальные теоремы и вариационные уравнения для статической и динамической связанной термоупругости.