1. Разрешающие уравнения Инженерных задач механики

Исследование различных явлений в механике твердого деформируемого тела (сопротивлении материалов, строительной механике и теории упругости), механике жидкости и газа (аэрогидромеханике) и механике тепломассопереноса (термодинамике и теплотехнике) на определенном этапе сводится к решению математических задач, включающих, как правило, дифференциальные уравнения. Эти уравнения описывают поведение некоторой физической модели, аппроксимирующей реальное физическое явление (работу конструкции, теплообмен изделия с окружающей средой, изменение параметров потока жидкости или газа).

Математические задачи механики представляют собой краевые задачи или задачи с известными условиями в начале исследуемого процесса для одного или нескольких дифференциальных уравнений с одним или несколькими независимыми переменными.

Точное решение этих задач можно подучить лишь в немногих простых случаях. Большинство же практически важных задач не удается решить точно либо из-за трудоемкости и громоздкости выкладок, либо из-за невозможности постановки задачи в какой-либо удобной функциональной форме, либо по причине трудности удовлетворения граничным условиям. Кроме того, могут быть неизвестны функции, являющиеся решениями полученных дифференциальных уравнений.

В этих случаях на помощь приходят различные методы приближенного решения краевых задач. Среди них важное место занимают численные методы, в особенности метод конечных разностей и метод конечных элементов, дающие численные значения искомых функций (решений) при тех или иных значениях аргумента. Другую группу приближенных методов решения краевых задач составляют так называемые прямые методы, которые задачи интегрирования дифференциальных или интегральных уравнений сводят к конечным системам алгебраических уравнений. Изложению этих методов посвящено настоящее пособие.

Предварительно, до непосредственного изучения приближенных методов, целесообразно коротко остановиться на основных уравнениях задач механики.

1.1. Краевая задача теории упругости

Во всех краевых задачах теории упругости определяются напряжения и деформации упругого тела, подверженного действию внешних сил. Ограничимся в наших рассуждениях случаями, когда деформации тел не слишком велики, так что напряжения и деформации можно считать связанными линейным соотношением, известным под названием обобщенного закона Гука. Принятая гипотеза представляет собой обычную гипотезу классической линейной теории упругости, охватывающей большинство задач, привлекающих в настоящее время внимание специалистов по прочности. Имеются два основных типа этих задач. В задачах одного типа требуется определить поля напряжений и деформаций внутри тела, если заданы деформации на поверхности этого тела. Этот тип задач носит название первой основной краевой задачи теории упругости. Вторая основная задача представляет собой определение напряжений и смещений внутри некоторой конструкции, к поверхности которой приложено заданное распределение внешних сил. На практике часто встречается комбинация этих двух основных типов задач, когда на некоторой части поверхности деформируемого тела заданы смещения, а на остальной части поверхности тела заданы внешние силы.

Определение и обозначение напряжений. Если тело находится под действием внешних сил, то форма и размеры его изменяются, причем влияние сил распространяется на все тело. Выделим внутри тела малую плоскую площадку; действие сил передается через нее от части тела, находящейся по одну сторону площадки, на часть тела, находящуюся с другой ее стороны. Под напряжением понимается внутренняя сила, приходящаяся на единицу площади. Будем считать, что материал имеет непрерывное строение. Тогда напряжение σ, передающееся в некоторой точке через малую площадку , можно выразить как предел отношения –

σ = lim ∆F/∆A,

_∆A→0

где приходящаяся на площадку внутренняя сила.

Через любую точку можно провести бесконечное множество площадок. Для того чтобы определить напряжение, необходимо знать не только его величину, линию действия и направление, но также и площадку, по которой оно действует. Поэтому напряжение необходимо понимать как тензор: оно зависит не только от вектора усилия, но и от вектора, характеризующего соответствующую площадку. В произвольно выбранной прямоугольной системе координатных осей сила полностью определяется компонентами вдоль этих осей. Эти компоненты вдоль осей х, у, z удобно обозначать, присоединяя к букве F соответственно один индекс: . Однако такие обозначения недостаточны для напряжений; чтобы полностью охарактеризовать напряжение, нужно еще определить сечение, в котором напряжение действует. Для этого можно ввести второй индекс, соответствующий направлению нормали к плоскости сечения. Например, нормаль к сечению, параллельному плоскости уz, направлена вдоль оси х, поэтому для обозначения такого сечения можно использовать индекс х.

Напряжение в сечении, проходящем через некоторую точку, можно разложить на две составляющие – нормальное напряжение, перпендикулярное к сечению, и касательное напряжение, лежащее в плоскости сечения. Принято обозначать нормальную составляющую напряжения через , а касательную – через . Направление нормальной составляющей является вполне определенным; здесь достаточно одного индекса, обозначающего соответствующую площадку. Касательную же составляющую напряжения можно снова разложить на два компонента по направлениям координатных осей, лежащих в плоскости сечения; поэтому для определения касательного напряжения необходимы два индекса: первый должен обозначать плоскость, в которой напряжение действует, а второй – направление напряжения. При этом, например, три составляющие напряжения, действующие в плоскости уz, следует обозначать через . Через любую точку тела можно провести три взаимно перпендикулярные координатные плоскости, так что всего получится девять составляющих напряжения. Обозначения для них указаны на рис. 1.1.

Примем следующее правило знаков. Нормальное напряжение будем считать положительным, если оно является растягивающим, т. е. если напряжение направлено от площадки, на которую оно действует. Сжимающее напряжение, направленное к площадке, будет тогда отрицательным. Как легко видеть, для сечения, расположенного подобно грани на рис. 1.1, нормальное напряжение будет положительным, если его направление совпадает с направлением координатной оси; между тем, для такого сечения, как , положительное нормальное напряжение обращено в сторону, обратную направлению оси.

Положительные направления для касательных напряжений условимся выбирать соответственно следующим образом. В площадке, подобной , где растягивающее напряжение совпадает с направлением одной координатной оси, касательные напряжения будем принимать положительными, если они действуют по направлениям двух других координатных осей. Если же растягивающее напряжение направлено обратно по отношению к оси, то положительные касательные напряжения будут также действовать в сторону, обратную положительным направлениям координатных осей. Следовательно, положительные направления компонентов напряжения, действующих на правую, переднюю и верхнюю грани элементарного кубика на рис. 1.1, должны совпадать с положительными направлениями координатных осей. Для левой, задней и нижней граней элемента положительными надо, напротив, считать напряжения, обратные направлениям осей.

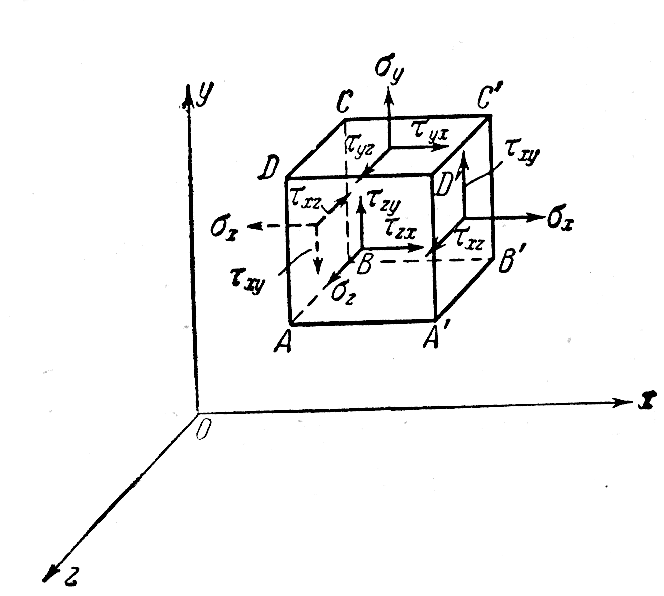
Риc. 1.1. Напряжения в упругом теле

Дифференциальные уравнения равновесия в напряжениях. Приложенные к телу внешние силы считаются уравновешенными, если при действии этих сил тело находится в состоянии покоя или прямолинейного равномерного движения. Различают, вообще говоря, два рода внешних сил: поверхностные и объемные силы. Например, гидростатическое давление, распределенное по поверхности тела, относится к поверхностным силам. С другой стороны, сила веса и центробежная сила, распределенные по объему тела, являются объемными. Поверхностную силу относят к единице площади, а объемную силу к единице объема. Чтобы различать эти два рода сил, условимся обозначать компоненты поверхностной силы вдоль осей х, у, z через а компоненты объемной силы через X, У, Z.

Прежде, чем перейти к составлению уравнений равновесия, выпишем выражения для составляющих напряжения в различных площадках бесконечно малого элемента. Выделим элемент длиной, равной единице, и площадью поперечного сечения . В общем случае напряжения в теле меняются от точки к точке. Рассмотрим простой случай, когда тело подвергается действию растягивающих напряжений только в направлении х (рис. 1.2, а). Обозначим напряжение в точке А через . Так как через обозначен бесконечно малый линейный элемент, то напряжение в точке В, равное можно представить как сумму и малого приращения напряжения на отрезке от А до В. Это малое приращение можно определить по известному правилу дифференциального исчисления: скорость изменения по координате х, относящуюся к точке А, надо умножить на длину отрезка АВ –

. (1.1)

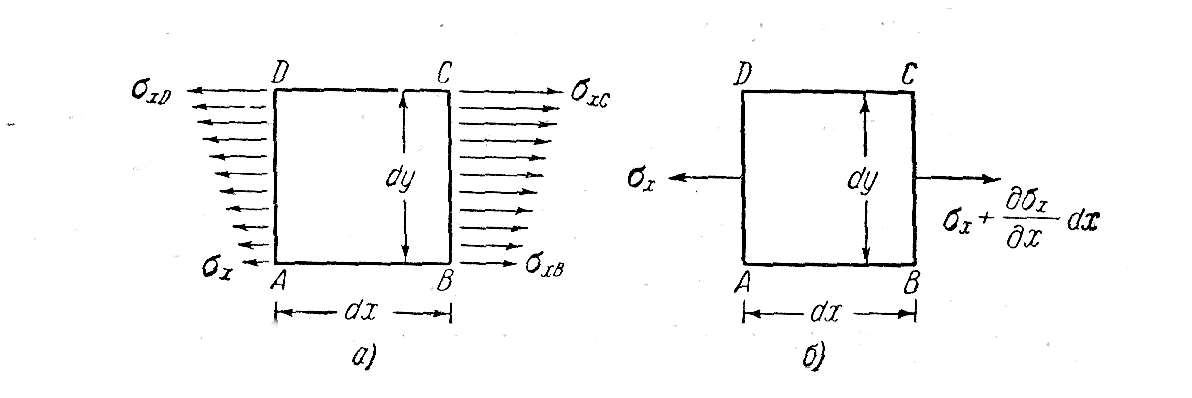
Рис. 1.2. Растяжение в направлении оси x

В выражении (1.1) используется символ частной производной, так как зависит не только от координаты х, но и от у. Выражения для напряжений в точках D и С запишутся аналогичным образом –

; (1.2)

(1.3)

Поскольку величины dх и dу являются бесконечно малыми, их квадраты или произведения надо рассматривать как величины второго порядка малости. Поэтому в выражении (1.3) можно было пренебречь членом по сравнению с остальными членами.

Когда мы пренебрегаем членами высшего порядка, то допускаем тем самым, что вдоль граней АD и ВС напряжения распределяются по линейному закону. Сила, действующая в сечении АD, будет при этом равна –

Аналогичным образом находим силу в сечении ВС –

Результирующая сила, действующая на элемент АВСD, будет равна –

Если предположить, что среднее напряжение по АD равно σ_х и приложено в центре грани, то среднее напряжение по ВС будет σ_x + (∂σ_x/∂x)∙dx.

Что касается результирующей силы, то это второе предположение о равномерном распределении напряжений приводит к тому же результату, что и первое. В уравнения равновесия входят, прежде всего, эти результирующие силы. Таким образом, при выводе уравнений равновесия можно взамен первого, более детального подхода, пользоваться вторым предположением, упрощая закон распределения напряжений.

На рис. 1.3 показан более общий случай, когда тот же элемент находится в двухосном напряженном состоянии, причем усилия считаются положительными и принят упрощенный закон их распределения; изображены также объемные силы. Под двухосным напряженным состоянием понимается случай, когда не зависят от z, а остальные компоненты напряжения равны нулю. Объемные силы X и Y принимаются не зависящими от z, величина Z считается равной нулю. Такое напряженное состояние называют плоским. Суммируя проекции всех сил на направление х и пользуясь условием , получим –

Приводя подобные члены, находим –

Произведение , вообще говоря, не равно нулю; поэтому условие сводится к уравнению –

(1.4)

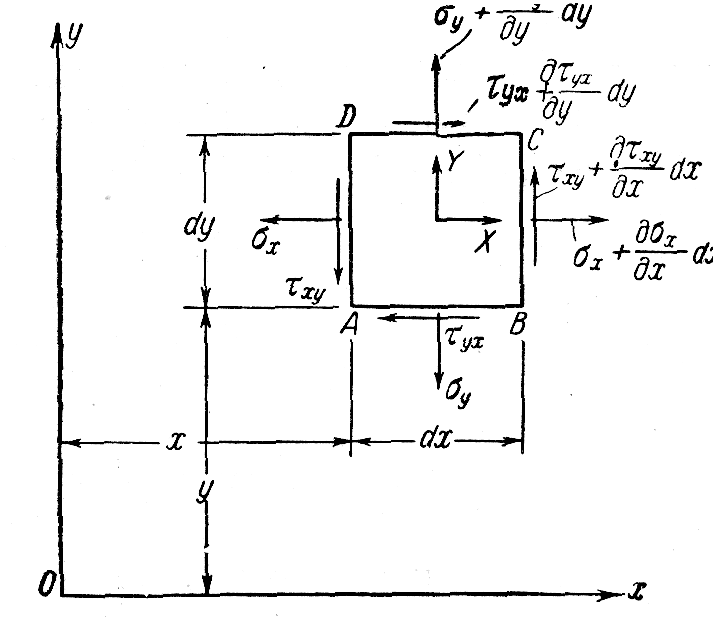
Рис. 1.3. Двухосное напряженное состояние

Таким же образом из условия получаем –

(1.5)

Уравнения (1.4) и (1.5) являются основными дифференциальными уравнениями равновесия в напряжениях, записанными в декартовых координатах.

Обратимся к наиболее общему случаю элемента, находящегося под действием положительных усилий в трех направлениях. Как легко показать, дифференциальные уравнения равновесия в декартовых координатах примут тогда вид –

. (1.6)

Обратимся к рис. 1.3 и определим моменты всех сил относительно точки 0; исходя из условия , будем иметь –

(1.7)

Согласно равенствам (1.4) и (1.5) выражения во второй и третьей скобках уравнения (1.7) обращаются в нуль. Так как произведение dхdу, вообще говоря, не равно нулю, уравнение (1.7) преобразуется к виду –

или

(1.8)

Рассматривая общий случай объемного напряженного состояния и определяя моменты сил, действующих на элемент, относительно осей z, у и х, получим –

(1.9)

Равенства (1.9) показывают, что компоненты касательных напряжений симметричны. Выше говорилось о девяти различных составляющих напряжения, действующих по трем координатным плоскостям в любой точке тела. Теперь мы знаем, что из шести касательных компонентов напряжений только три являются независимыми. Равенства (1.9) принято называть законом парности касательных напряжений.

Компоненты деформации. Под деформацией тела подразумевается изменение взаимного положения точек тела. Примем координаты точки тела до деформации х, у, z. В процессе деформации тела эта точка получает перемещения и, v, w по направлениям х, у, z и в результате будет иметь координаты . В общем случае перемещения и, v,w меняются от точки к точке и потому являются функциями х, у, z.

Начнем исследование деформаций со случая двухмерной или плоской деформации. Под ней понимают такую деформацию, при которой все частицы, находившиеся первоначально в одной плоскости, останутся после деформации в этой же плоскости. Пусть координатные оси выбраны так, что оси х и у лежат в плоскости деформации; тогда w = 0, а и и v не зависят от z. Рассмотрим малый прямоугольный элемент АВСD недеформированного тела со сторонами dх и dу (рис. 1.4). После деформации элемент перемещается в положение А'В'С'D'. С геометрической точки зрения можно различать два основных типа деформации: изменения длины первоначально прямой линии в определенном направлении и изменение величины первоначального прямого угла.

В соответствии с этим различают продольную деформацию и деформацию сдвига.

Отношение изменения длины к первоначальной длине элементарного отрезка определяется как продольная деформация; ее обозначают буквой . В случае сплошного материала деформацию в любой точке тела можно выразить через начальную длину отрезка как предел отношения –

где изменение длины отрезка.

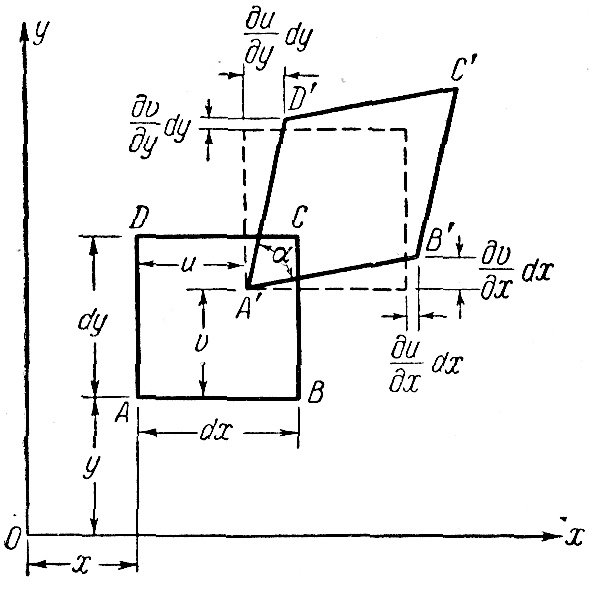
Рис. 1.4. Деформации элемента

Изменение величины первоначально прямого угла называют деформацией сдвига и обозначают через . В случае прямоугольного элемента АВСВ, показанного на рис. 1.4, до деформации длина отрезка [АВ] была равна dх. После деформации точка А переместилась в А'. Обозначим составляющие перемещения точки А вдоль осей х, у через и и v. Так как величины и и v изменяются в теле от точки к точке, их можно разложить в ряд Тейлора. Отбрасывая члены высшего порядка малости, можно записать составляющие перемещения из В в В' в виде и . Таким образом, проекция отрезка [А'В'] на ось х равна , а проекция на ось у окажется равной . Квадрат длины отрезка [А'В'] будет –

Составляющая по оси х продольной деформации определяется как продольная деформация элемента, направленного до деформации вдоль оси . Поэтому можно записать –

и

Подставив эту величину в выражение для и разделив на , получим –

(1.10)

Будем рассматривать случай, когда деформации тела весьма малы. Тогда величины и производные от и будут малыми. Поэтому квадратами и произведениями этих величин можно пренебрегать по сравнению с самими величинами. Отбрасывая члены высшего порядка малости в выражении (1.10), имеем –

Подобным же образом найдем составляющую продольной деформации в направлении оси y –

Чтобы определить деформацию сдвига, рассмотрим искажение первоначально прямого угла. Деформация сдвига в точке определяется как изменение величины угла между двумя элементарными отрезками, первоначально параллельными осям х и у. Следовательно, величина в точке А представляет собой изменение угла между отрезками [АВ] и [АD]. Перемещение точки В' в направлении у равно а перемещение точки и в направлении х равно Пренебрегая членами высшего порядка малости, находим, что линия АВ, занимая после деформации положение А'В', окажется наклоненной к ее начальному направлению под малым углом , а направление А'В' будет наклонено к АD под малым углом .

Как видим, прямой угол DАВ между отрезками [АВ] и [АD] уменьшился на угол . Отсюда –

.

Компоненты деформации для трехмерной задачи можно получить таким же образом. Они будут равны –

(1.11)

Шесть величин называются компонентами деформации. Из этих формул легко видеть, что деформации сдвига обладают симметрией –

.

Уравнение совместности деформаций. Легко заметить, что в уравнениях (1.11) шесть компонентов деформаций выражены через три компонента перемещений. Тот факт, что компоненты деформации не могут быть выбраны произвольно, очевиден из тех геометрических соображений, что они описывают относительные смещения точек единого сплошного деформированного тела. Чтобы обеспечить условие сплошности тела, компоненты деформации для каждого элемента должны удовлетворять определенным соотношениям. Продифференцировав выражение –

по х и у, получим –

Так как x и у являются однозначными непрерывными функциями, это выражение можно переписать следующим образом –

Пользуясь зависимостями и , получим –

(1.12)

Продифференцируем далее выражение для по и , выражение для по у и х, а затем сложим полученные выражения; тогда будем иметь –

Используя, по-прежнему, то обстоятельство, что и, v и w являются однозначными непрерывными функциями, можно придать этой зависимости следующий вид –

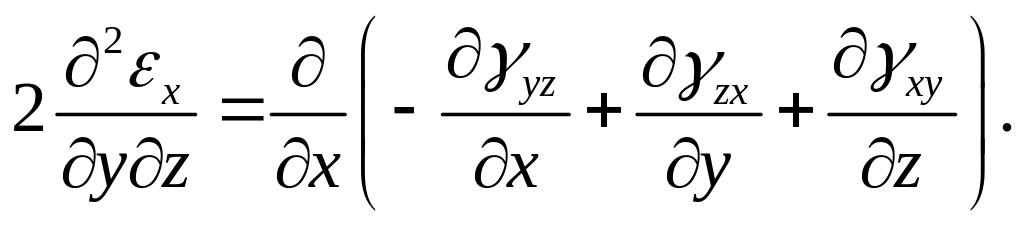(1.13)

Другие подобные зависимости могут быть получены циклической перестановкой. В результате придем к шести зависимостям, которым должны удовлетворять компоненты деформации –

(1.14)

Эти дифференциальные уравнения называют уравнениями совместности деформаций.

Обобщенный закон Гука. Все тела, находящиеся в напряженном состоянии, получают деформацию. Зависимость между деформацией и приложенной силой впервые была сформулирована Гуком. Закон Гука о пропорциональности между силами и перемещениями гласит, что «удлинение пропорционально силе», и в нем идет речь о средней величине удлинения тонкого стержня, подвергающегося действию растягивающего усилия.

Естественно обобщить закон Гука на случай объемного напряженного состояния при условии, что предел упругости не превзойден: в любой точке сплошной среды каждый из шести компонентов напряжения является линейной функцией шести компонентов деформации, и наоборот. Это положение называется обобщенным законом Гука. Выражая его математически, получим шесть зависимостей для деформаций от напряжений –

(1.15)

В этих соотношениях Е – модуль упругости материала, G – модуль сдвига, равный –

(1.16)

Уравнения равновесия в напряжениях. Для постановки конкретной задачи теории упругости по определению характеристик напряженно-деформированного состояния тепа под действием заданной нагрузки выше получены все необходимые соотношения. Действительно, неизвестные величины шести напряжений σ_x, σ_y, σ_z, τ_xy, τ_yz, τ_xz, деформаций и перемещений u, v, w принципиально могут быть определены совместным решением системы уравнений равновесия в напряжениях (1.6), соотношений закона Гука (1.15) и геометрических условий связи между деформациями и перемещениями (1.11). Вместе с тем, эти соотношения позволяют выразить все неизвестные величины через три перемещения u, v, w, сведя тем самым систему пятнадцати уравнений с пятнадцатью неизвестными к трем уравнениям равновесия в перемещениях. Опуская промежуточные выкладки, запишем эту систему в виде –

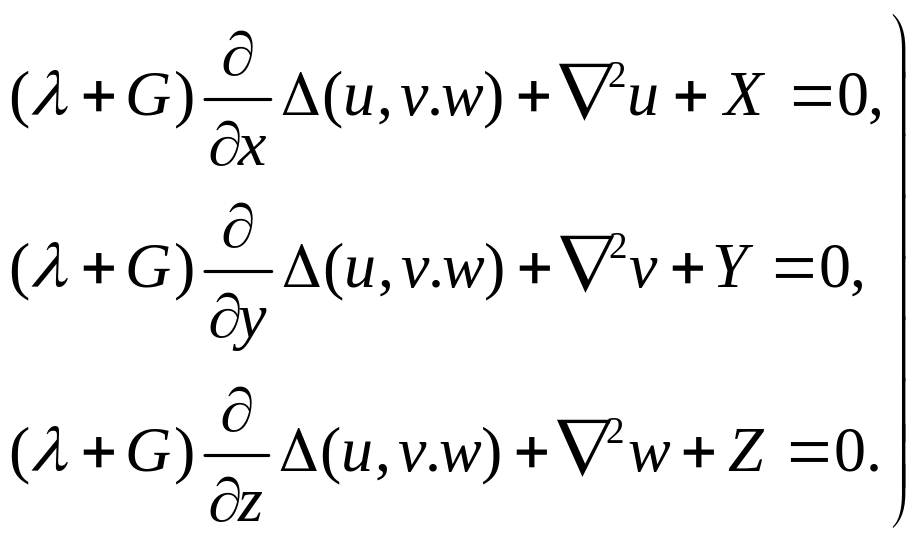(1.17)

или –

(1.18)

Здесь коэффициент Ламе, μ – коэффициент поперечного сжатия Пуассона, модуль сдвига, определяемый формулой (1.16), , массовая плотность материала, составляющие массовых сил.

Система (1.17) является системой уравнений движения упругого тела, т. к. содержит выраженные через вторые производные перемещений по времени составляющие сил инерции д’Аламбера.

При формулировке задачи теории упругости могут быть известны не поверхностные силы на границе, а перемещения u, v, w точек граничной поверхности. Граничные условия могут также заключаться в том, что на одной части границы будут заданы поверхностные силы, а на другой – перемещения. Уравнения (1.18) совместно с граничными условиями полностью определяют три компонента перемещения u, v, w. При этом нет нужды пользоваться уравнениями совместности, т.к. единственное назначение последних состоит в том, чтобы наложить ограничения на компоненты деформации, обеспечив однозначность и непрерывность перемещений.

К сожалению, точное решение уравнений теории упругости возможно для очень ограниченного круга задач. К ним относятся задача определения напряженно-деформированного состояния цилиндра с плоскими торцами, задача расчета растяжения-сжатия пластины, задача о полубесконечной плоскости и упругом клине.

В остальных случаях приходится прибегать к использованию тех или иных приближенных методов.