4. Задание № 3
Цель решения задачи по заданию №3 – научиться формулировать математическую постановку задачи оптимизации на основе имеющейся математической модели реального технического объекта и овладеть приемами решения задачи НЛП. В качестве объекта рассматривается процесс одноинструментальной обработки вала.
1. Математическая модель описывает основные показатели качества одноинструментальной обработки гладкого вала на токарном станке и включает в себя зависимости, связывающие показатели качества с параметрами объекта.
Производительность обработки Q:
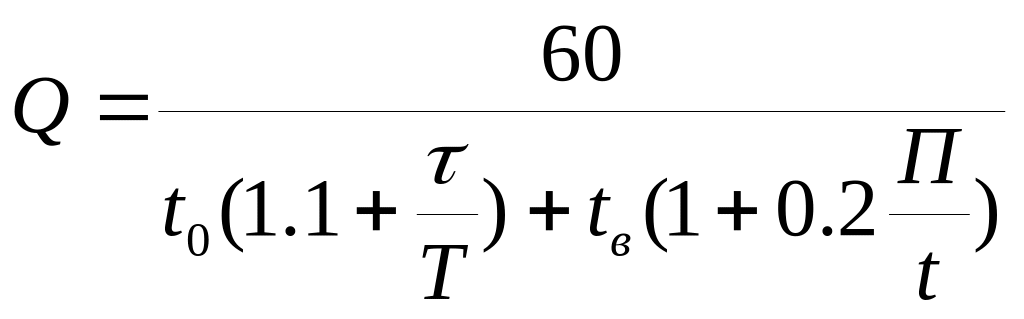(шт/час),
(4.1)
где
t0
=
(мин),
n
=
(об/мин),
Т
– стойкость
режущего инструмента:
(мин),
(4.2)
L – длина рабочего хода, мм, n – частота вращения детали, об/мин, S – скорость подачи инструмента на один оборот детали, мм/об, V – скорость резания, м/мин, D – диаметр обработки, мм, П - припуск на обработку, мм.
Сила резания Pz:
Pz = 2000 S0.75 t , Н, (4.3)
Мощность резания N:
N = 0.0325 V S 0.75 t, кВт. (4.4)
Стойкость режущего инструмента - определяется по (4.2).
Шероховатость обработанной поверхности Rа :
,мкм.
(4.5)
Таблица 4
Исходные данные для решения задачи
№ вар. |
nmax , об/мин |
L, мм |
D, мм |
П, мм |
t, мм |
Tдоп, мин |
, мин |
Pz доп, Н |
Nдоп (Nдвиг), квт |
Ra доп, мкм |
1 |
1600 |
200 |
50 |
6 |
6 |
20 |
10 |
8000 |
12 |
12,8 |
2 |
10000 |
200 |
80 |
2 |
1 |
30 |
15 |
2000 |
8 |
1,6 |
3 |
6000 |
300 |
40 |
3 |
3 |
30 |
15 |
5000 |
10 |
6,4 |
4 |
3000 |
400 |
80 |
8 |
8 |
25 |
20 |
10000 |
12 |
6,4 |
5 |
12000 |
100 |
20 |
1 |
0,5 |
30 |
15 |
3000 |
12 |
0,8 |
6 |
5000 |
250 |
50 |
3 |
2 |
25 |
15 |
6000 |
10 |
3,2 |
7 |
4000 |
200 |
40 |
5 |
5 |
40 |
15 |
9000 |
11 |
12,8 |
8 |
9000 |
200 |
30 |
3 |
1,5 |
35 |
20 |
4000 |
10 |
1,6 |
9 |
5000 |
300 |
40 |
4 |
4 |
30 |
15 |
6000 |
12 |
6,4 |
10 |
2500 |
400 |
60 |
8 |
8 |
25 |
20 |
12000 |
15 |
6,4 |
11 |
15000 |
300 |
20 |
1 |
0,3 |
20 |
10 |
3000 |
8 |
0,8 |
12 |
4000 |
450 |
30 |
2 |
2 |
50 |
10 |
5000 |
8 |
3,2 |
13 |
6000 |
200 |
80 |
5 |
5 |
45 |
15 |
11000 |
12 |
12,8 |
14 |
15000 |
300 |
50 |
1 |
0,5 |
40 |
15 |
2000 |
10 |
0,8 |
15 |
7000 |
300 |
30 |
4 |
4 |
45 |
10 |
6000 |
10 |
6,4 |
16 |
3000 |
300 |
50 |
5 |
5 |
50 |
20 |
8000 |
12 |
6,4 |
17 |
12000 |
200 |
30 |
2 |
0,3 |
55 |
15 |
2000 |
12 |
0,8 |
18 |
5000 |
300 |
40 |
2 |
2 |
45 |
15 |
5000 |
8 |
3,2 |
19 |
3000 |
350 |
50 |
6 |
4 |
35 |
15 |
10000 |
11 |
12,8 |
20 |
10000 |
250 |
20 |
1.6 |
0,4 |
30 |
15 |
3000 |
10 |
0,8 |
Окончание табл.4 |
||||||||||
№ вар. |
nmax , об/мин |
L, мм |
D, мм |
П, мм |
t, мм |
Tдоп, мин |
, мин |
Pz доп, Н |
Nдоп (Nдвиг), квт |
Ra доп, мкм |
21 |
8000 |
300 |
30 |
6 |
4 |
25 |
10 |
5000 |
12 |
3,2 |
22 |
4000 |
150 |
40 |
7 |
7 |
20 |
10 |
12000 |
12 |
12,8 |
23 |
10000 |
300 |
25 |
3 |
1,5 |
25 |
15 |
2000 |
10 |
1,6 |
24 |
8000 |
400 |
20 |
2 |
2 |
30 |
15 |
6000 |
8 |
6,4 |
25 |
3000 |
200 |
50 |
4 |
4 |
35 |
15 |
9000 |
8 |
12,8 |
26 |
10000 |
300 |
80 |
4 |
2 |
40 |
15 |
2000 |
12 |
1,6 |
27 |
8000 |
250 |
30 |
3 |
2 |
45 |
20 |
6000 |
12 |
3,2 |
28 |
4000 |
300 |
50 |
8 |
8 |
50 |
10 |
14000 |
15 |
12,8 |
29 |
15000 |
200 |
20 |
2 |
0,3 |
45 |
15 |
2000 |
8 |
0,8 |
30 |
8000 |
300 |
30 |
2 |
2 |
40 |
15 |
4000 |
10 |
3,2 |
31 |
3000 |
150 |
100 |
6 |
6 |
35 |
10 |
12000 |
11 |
12,8 |
32 |
4000 |
200 |
90 |
5 |
5 |
30 |
15 |
11000 |
10 |
1,6 |
33 |
5000 |
250 |
80 |
6 |
4 |
25 |
15 |
8000 |
8 |
6,4 |
34 |
6000 |
300 |
70 |
3 |
3 |
20 |
20 |
6000 |
8 |
6,4 |
35 |
7000 |
350 |
60 |
5 |
2.5 |
25 |
15 |
4000 |
7 |
0,8 |
36 |
8000 |
400 |
50 |
4 |
2 |
30 |
15 |
3000 |
6 |
3,2 |
37 |
9000 |
450 |
40 |
3 |
1.5 |
35 |
15 |
2000 |
5 |
12,8 |
38 |
10000 |
500 |
30 |
2 |
1 |
40 |
20 |
1500 |
4 |
1,6 |
39 |
11000 |
450 |
40 |
1 |
0.5 |
45 |
15 |
1500 |
4 |
6,4 |
40 |
12000 |
300 |
50 |
1 |
1 |
50 |
20 |
2000 |
6 |
6,4 |
41 |
13000 |
250 |
40 |
1 |
0.5 |
55 |
10 |
2500 |
6 |
0,8 |
42 |
14000 |
200 |
30 |
2 |
0.5 |
50 |
10 |
2000 |
5 |
3,2 |
43 |
15000 |
150 |
25 |
0.6 |
0.3 |
45 |
15 |
2500 |
5 |
12,8 |
44 |
6000 |
200 |
80 |
7 |
7 |
40 |
15 |
8000 |
10 |
0,8 |
45 |
7000 |
250 |
70 |
6 |
6 |
35 |
10 |
7000 |
9 |
6,4 |
46 |
8000 |
300 |
60 |
10 |
5 |
30 |
20 |
12000 |
12 |
6,4 |
47 |
9000 |
350 |
50 |
8 |
4 |
25 |
15 |
6000 |
10 |
0,8 |
48 |
10000 |
400 |
45 |
3 |
3 |
20 |
15 |
5000 |
8 |
3,2 |
49 |
5000 |
450 |
60 |
4 |
4 |
25 |
15 |
3000 |
6 |
12,8 |
50 |
4000 |
500 |
70 |
5 |
5 |
30 |
15 |
4000 |
8 |
0,8 |
tв = 2 мин для всех вариантов |
||||||||||
Методические указания.
Чтобы сформулировать оптимизационную постановку задачи, нужно выбрать критерий оптимальности, управляемые параметры, ограничения.
Управляемые параметры. Данная задача используется при расчетах режима работы оборудования. Поэтому управляемыми параметрами будут элементы режима резания: подача S и скорость резания V.
Критерий оптимальности и функциональные ограничения. Они могут быть получены из набора показателей качества работы системы (4.1)… (4.5). В соответствии с тем, как сформулированы требования на показатели качества (табл.4), можно понять, какие показатели качества использовать в качестве критерия оптимальности, какие – в виде функциональных ограничений.
Судя по исходным данным, мы имеем информацию по допускаемым значениям силы резания, мощности, шероховатости и стойкости. Так, например, если значение силы резания, полученное при определенных значениях параметров, будет большим, чем допускаемое, то система будет неработоспособна и возможна поломка инструмента. Поэтому, текущее значение силы не должно превышать допускаемого: P z P z доп.
Аналогично можно получить вид всех функциональных ограничений.
Те (или тот) показатели качества, на которые нельзя сформулировать ограничения по типу «не более», можно использовать в качестве критерия оптимальности.
Прямые ограничения. В качестве прямых ограничений можно использовать паспортные данные станка по предельным значениям подач и оборотов шпинделя. Для всех вариантов :
12,5 ≤ n ≤ n max (об/мин), (4.6)
0.07 ≤ S ≤ 4.16 (мм/об). (4.7)
При этом следует помнить, что параметры n и V взаимозависимы, поэтому прямое ограничение (4.6) должно быть выражено через V (см. формулу 4.1).
Решение задачи. При поиске оптимального значения рекомендуется использовать один из методов поиска: метод покоординатного спуска, метод конфигураций или их сочетание [1, с.71-72].