5.2. Производные высших порядков от функций, заданных параметрически
Пусть функция y, зависящая от x, задана параметрически в интервале Т:
,
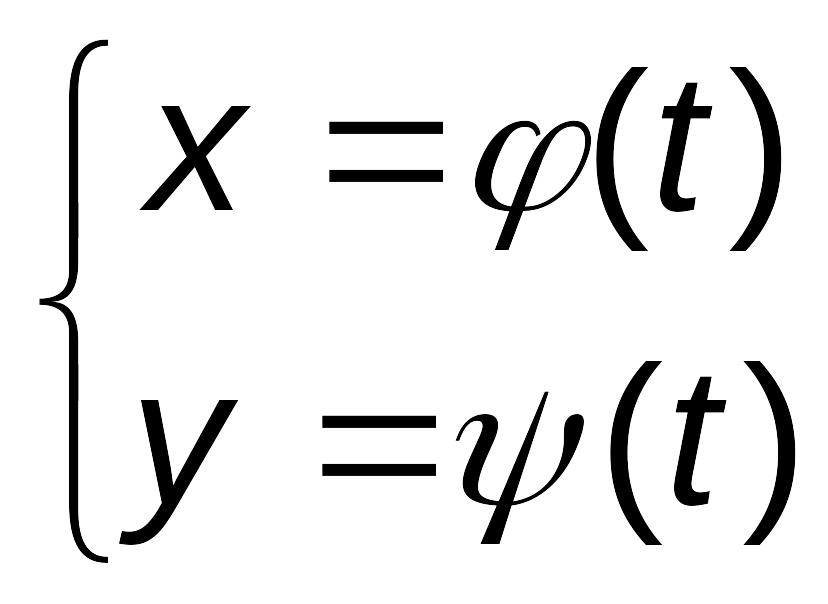Найдем
.
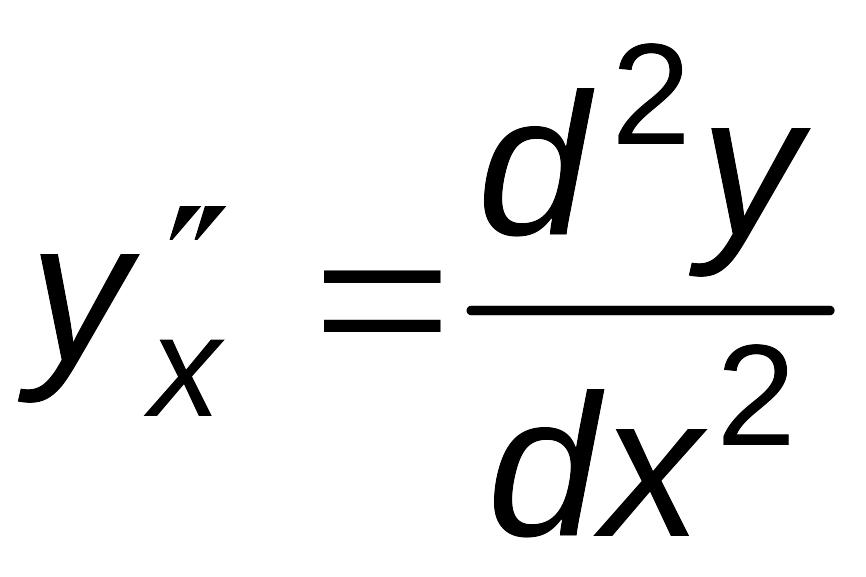Известно, что
=
=
(п. 4.3), поэтому
=
=
=
=
.
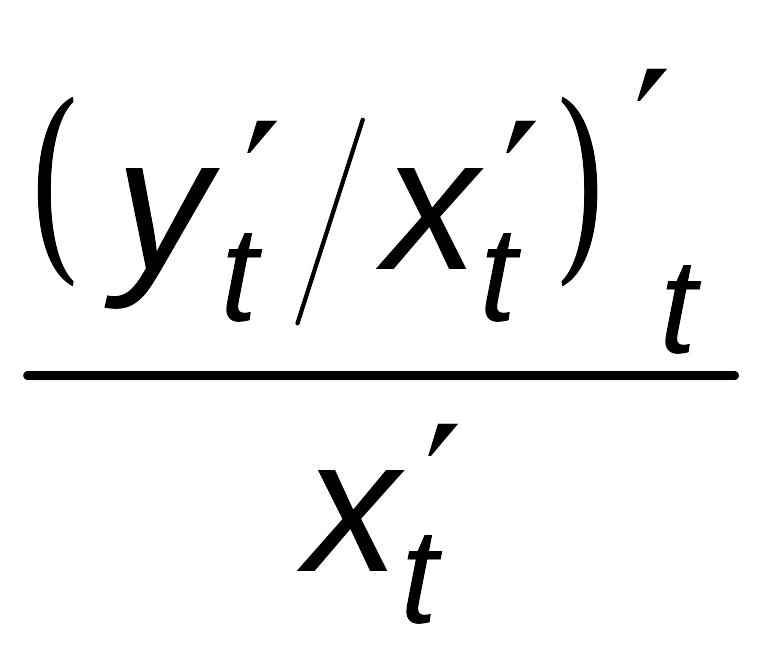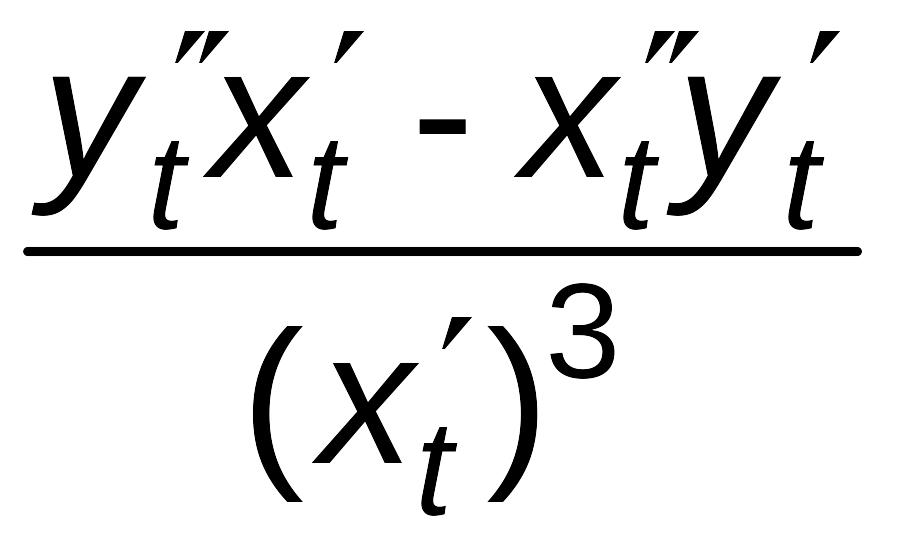Аналогично
будет вычисляться
и т. д.
Пример
5.3.
Найти
и
для функции, заданной параметрически:
.
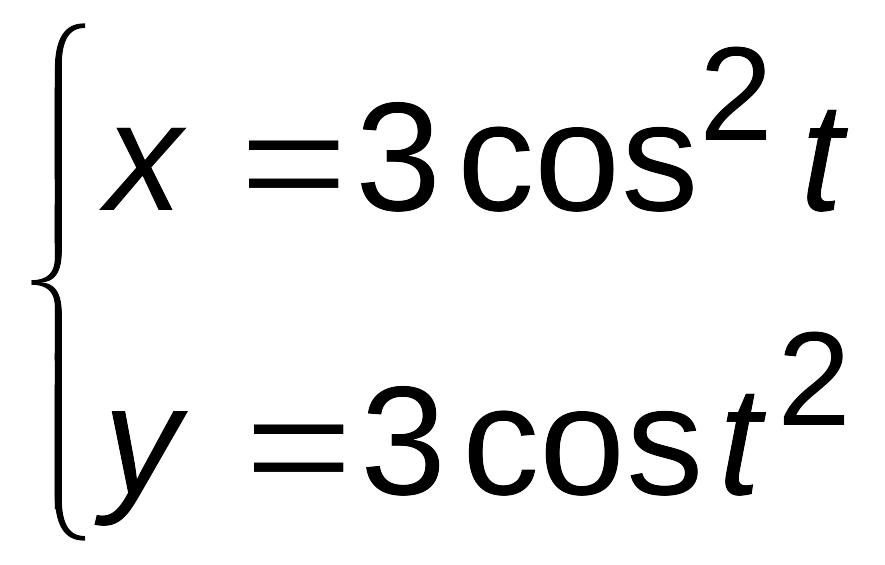Решение.
;
;
;
;
;
=
.
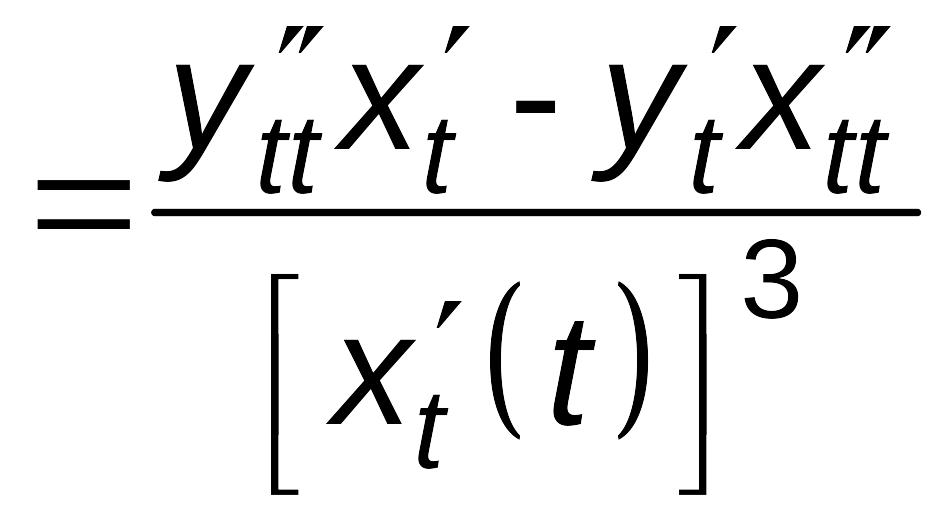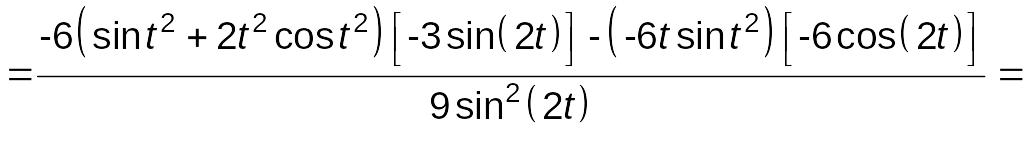
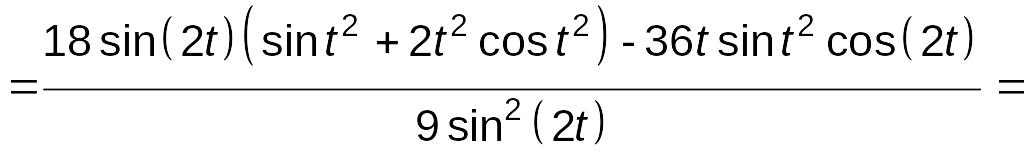
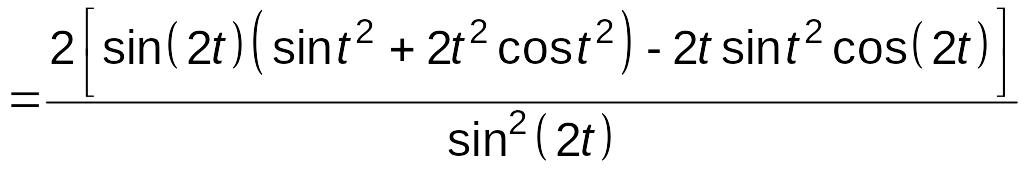Пример 5.4. Функция y от x задана параметрически уравнениями:
,
.
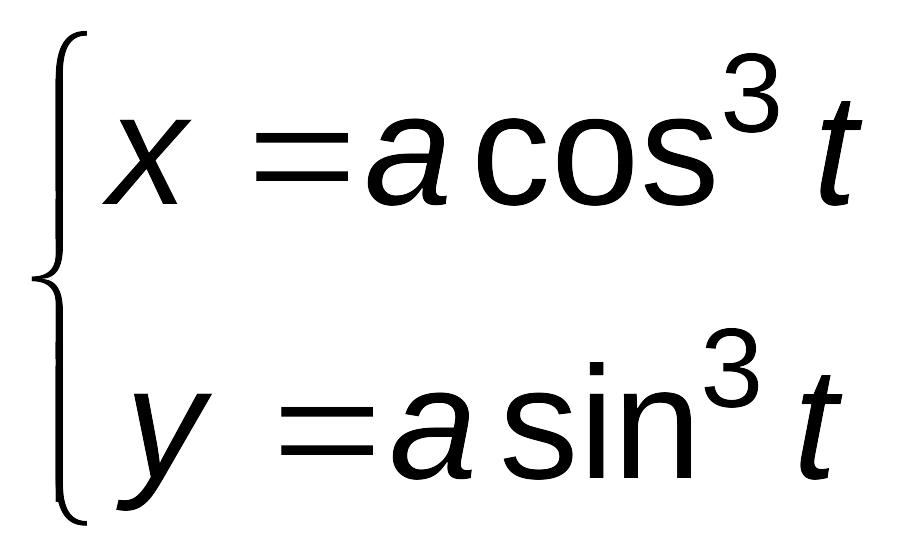Найти .
Решение.
=
=
=
=
;
=
=
=-
=
.
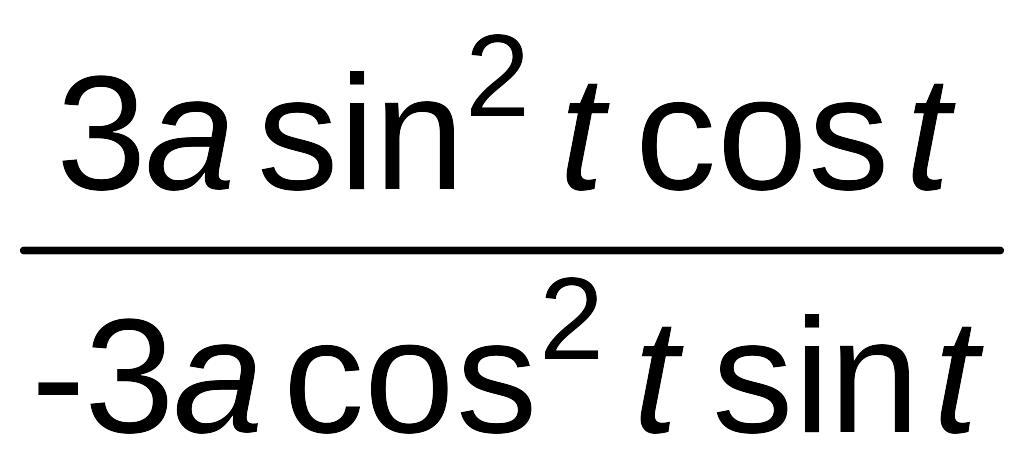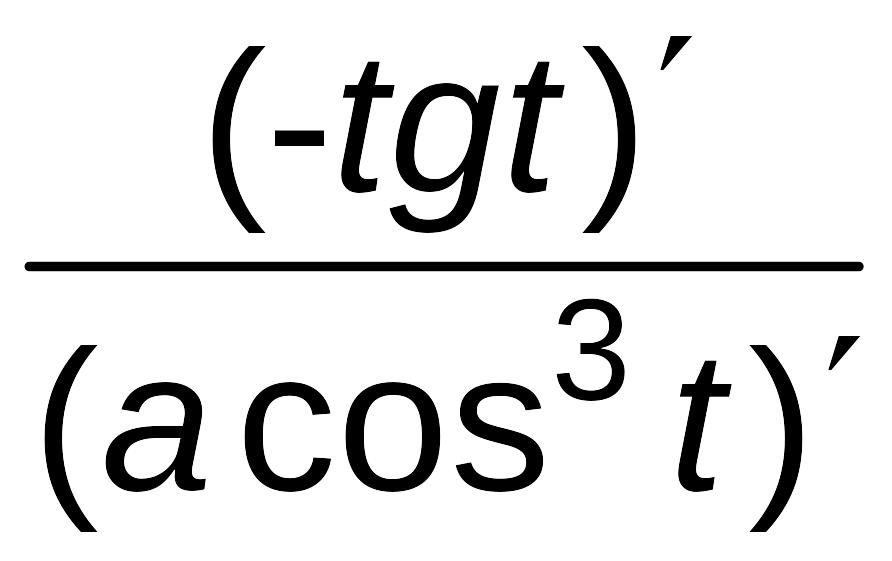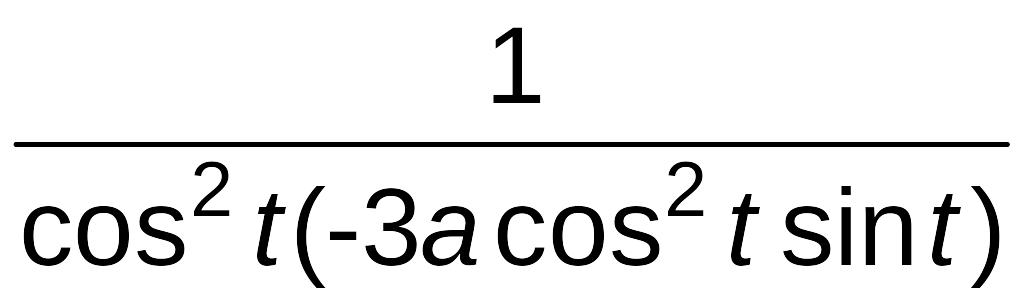5.3. Производные высших порядков от функций, заданных неявно
Нахождение производных высших порядков от функций, заданных неявно, рассмотрим на примере.
Пример
5.5.
Найти
,
для функции, заданной неявно уравнением:
.
Вычислить y'(0),
y''(0).
Решение.
Найдем сначала y', как описано в п. 4.2.
,
,
,
=
.
Для
нахождения y''
будем дифференцировать равенство
,
получим:
.
Отсюда
найдем y''
и подставим найденное выражение для y'
:
,
y''=–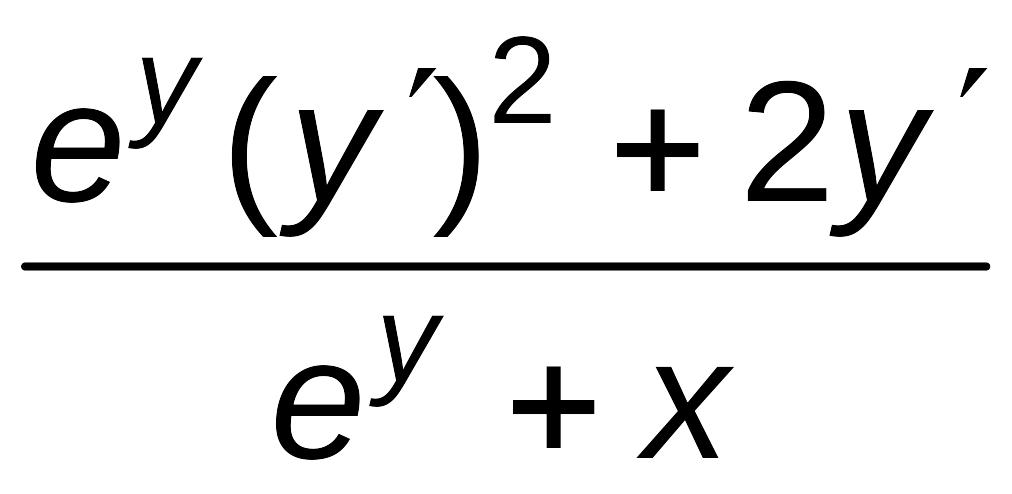
=
=
=
=
.
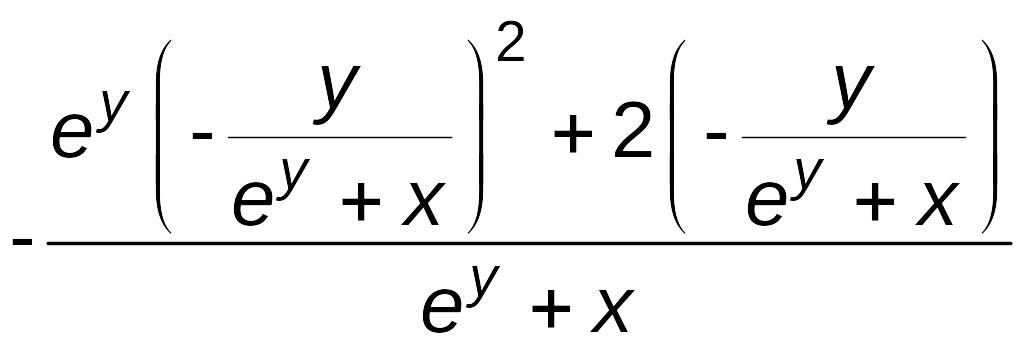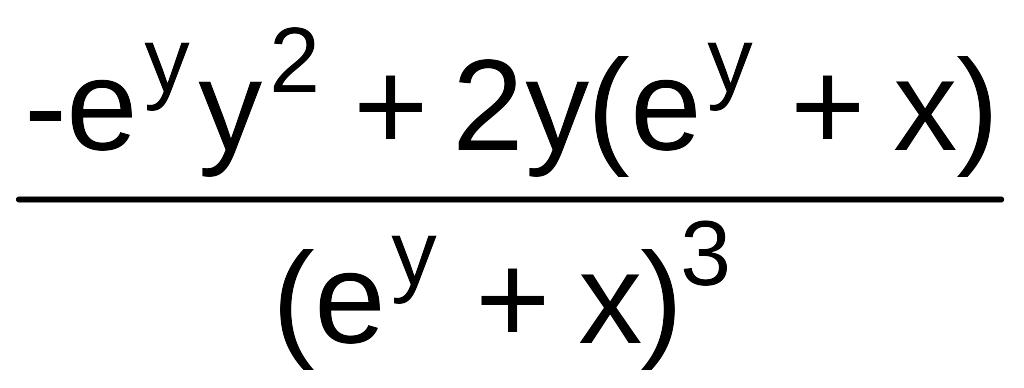Итак, y'=– , а y''= .
Подставим x=0 в исходное уравнение , получим:
,
откуда y=1,
значит
y(0)=1;
y'(0)=
–
;
y''(0)=
=
.
6. Правило Лопиталя
Рассмотрим
новый способ нахождения пределов
отношения двух бесконечно малых или
бесконечно больших функций, т. е.
раскрытия неопределенностей типа
и
,
так называемое правило
Лопиталя.
Теорема
Лопиталя 1
(раскрытие
неопределенностей типа
).
Пусть функции
,
определены, непрерывны и дифференцируемы
в точке x0
и некоторой ее окрестности, причем
для любого x
из этой окрестности, и пусть
,
(следовательно,
,
–
бесконечно малые при
).
Если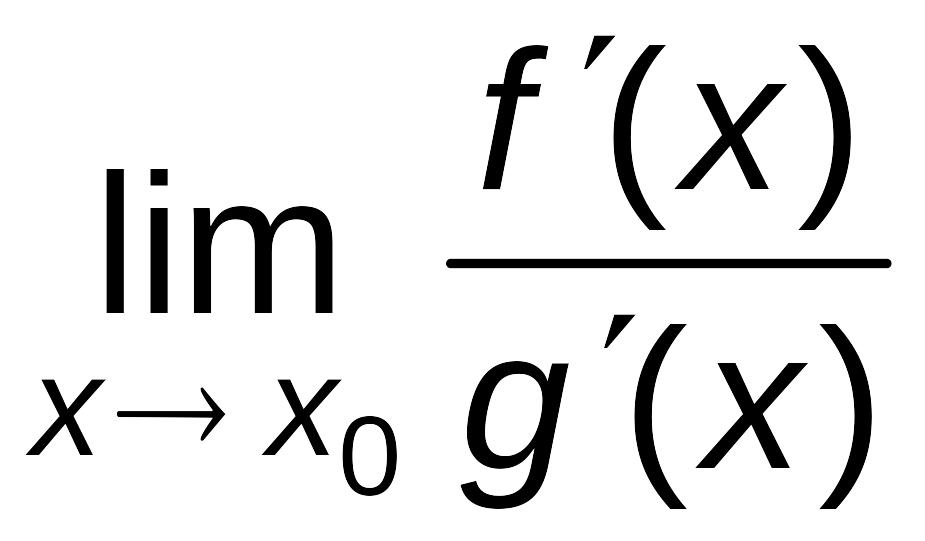
существует, то существует
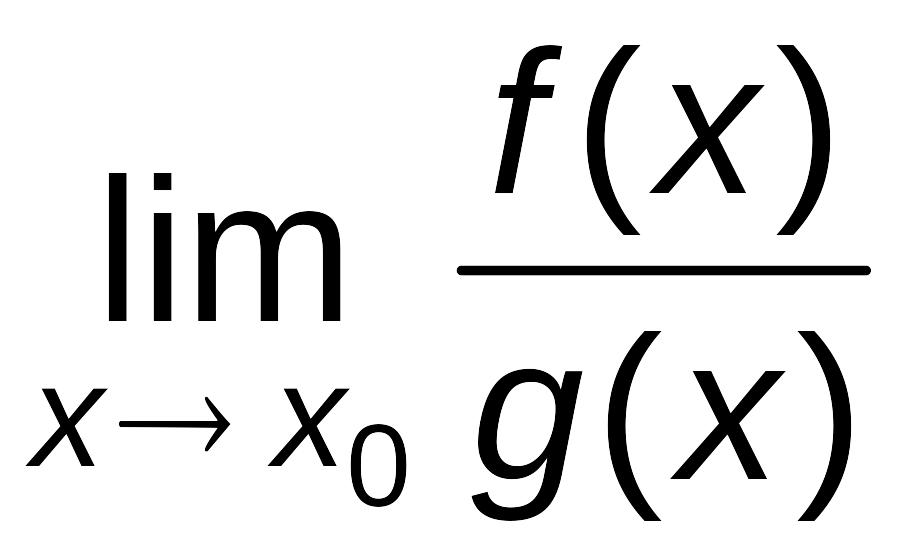и
= . (6.1)
Пример
6.1.
Найти
.
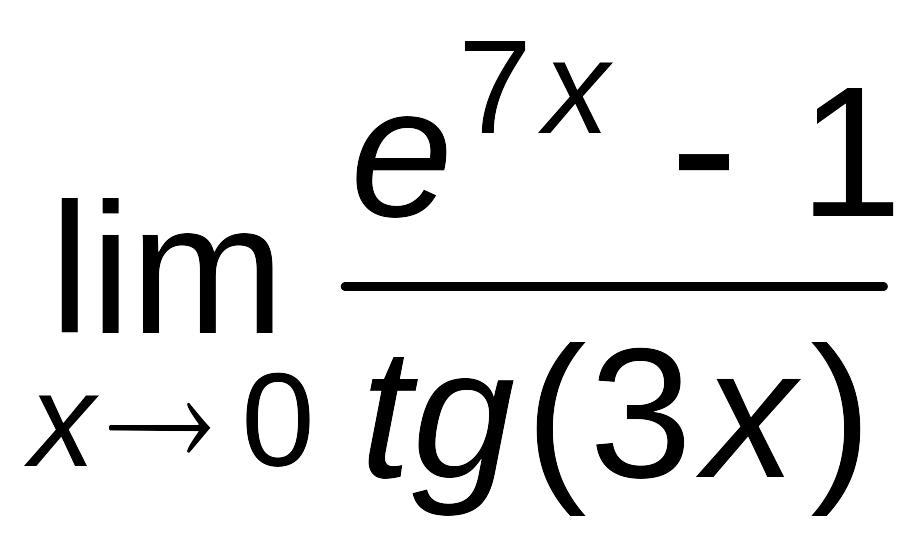Решение.
Так
как при
функции
и
,
то
имеем неопределенность типа
.
Числитель
и знаменатель данной дроби представляют
собой непрерывные дифференцируемые
функции в точке
.
Это означает, что можно применить правило
Лопиталя:
.
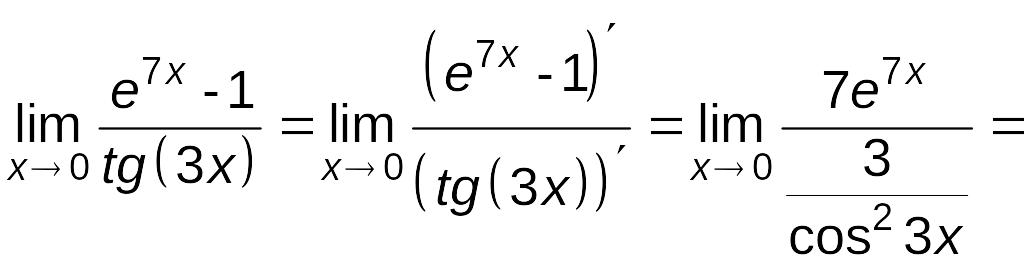
Пример
6.2.
Найти
.
Решение.
Поскольку
функции
и g(x)=2x
удовлетворяют условиям теоремы Лопиталя,
то
=
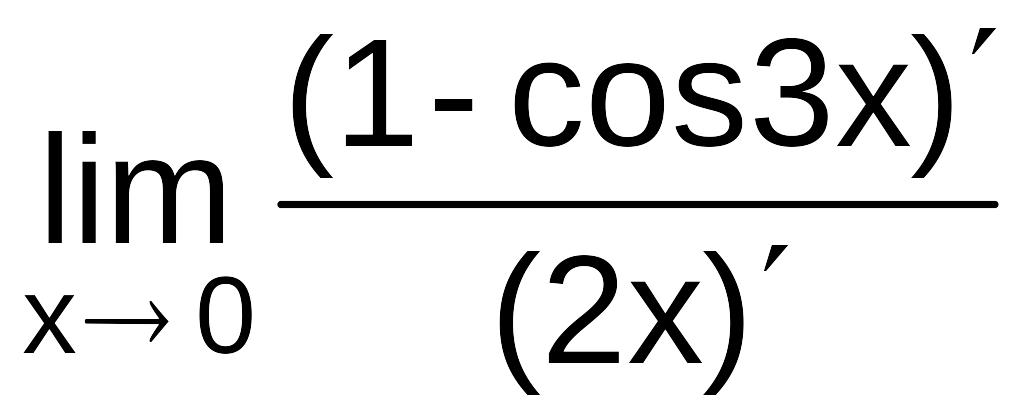
=0.
Замечание
1.
Теорема Лопиталя справедлива и в том
случае, когда функции
,
не определены в точке x0,
но
и
.
В
самом деле, если доопределить
и
,
положив
,
тогда
,
будут непрерывны в точке x0,
а потому теорема Лопиталя будет применима
к ним.
Замечание 2. Правило Лопиталя применимо и в том случае, когда
,
.
Действительно,
введя новую переменную
,
видим, что y→0
при x→.
Тогда
=
=
=
.
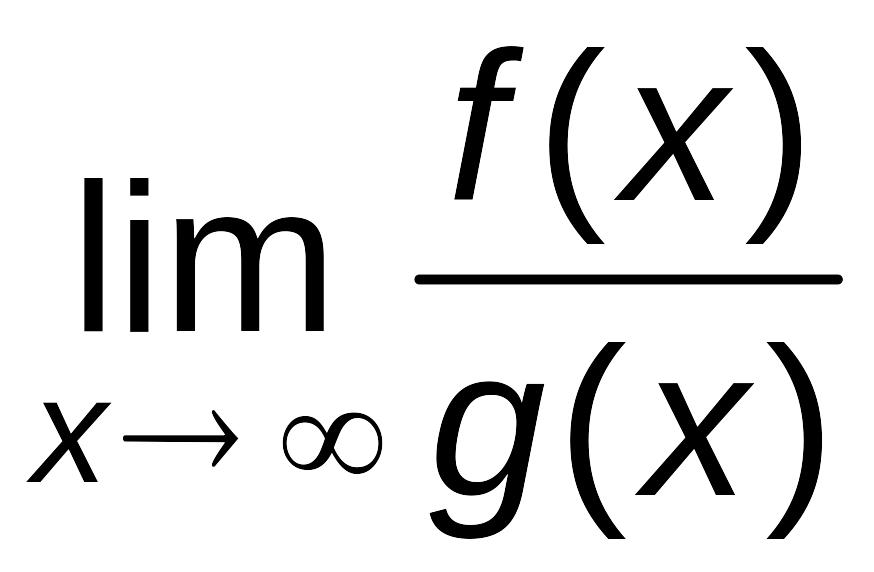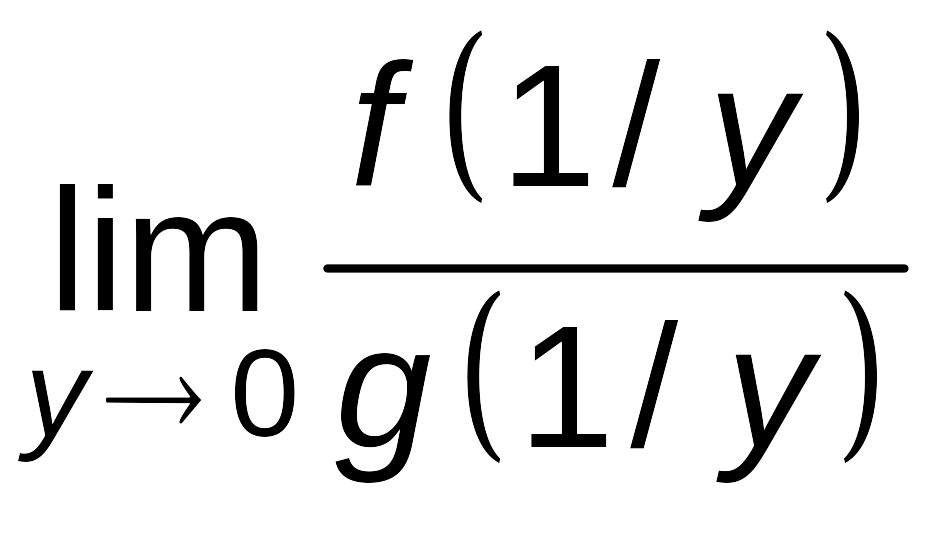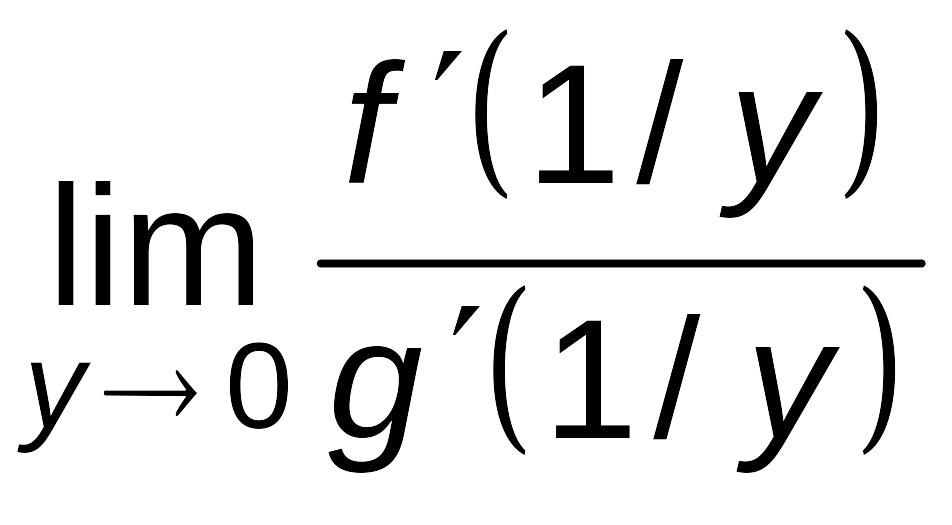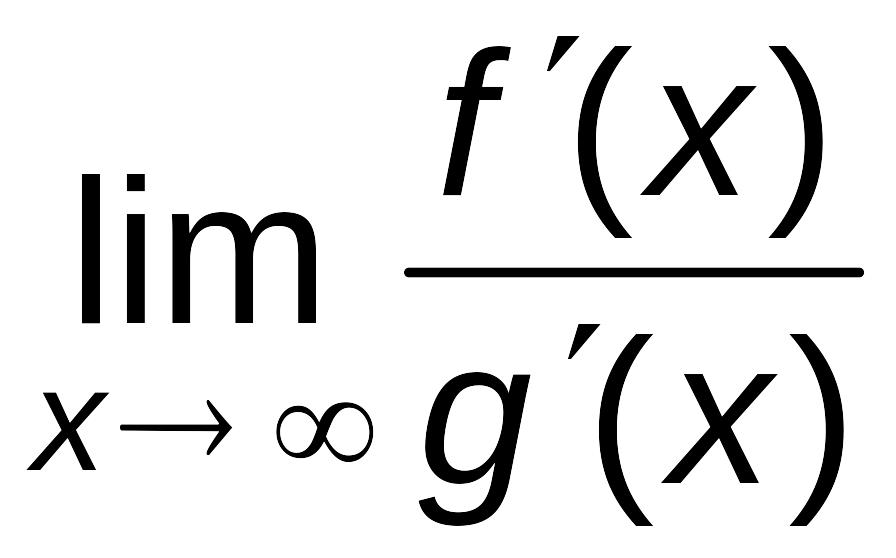Теорема Лопиталя (раскрытие неопределенностей типа .
Пусть
функции
,
дифференцируемы в окрестности точке
x0,
за исключением самой точки x0,
причем
,
и пусть
,
.
Если существует
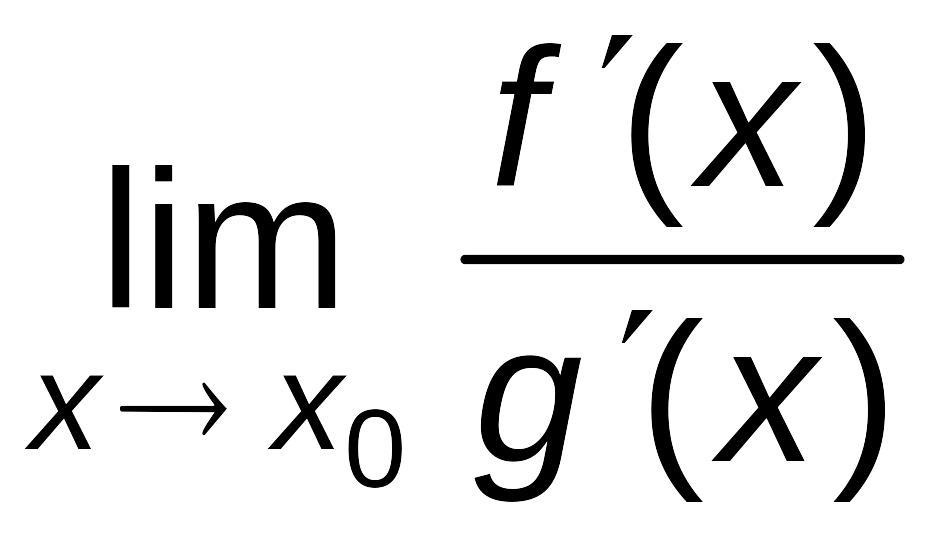то существует и
=
.
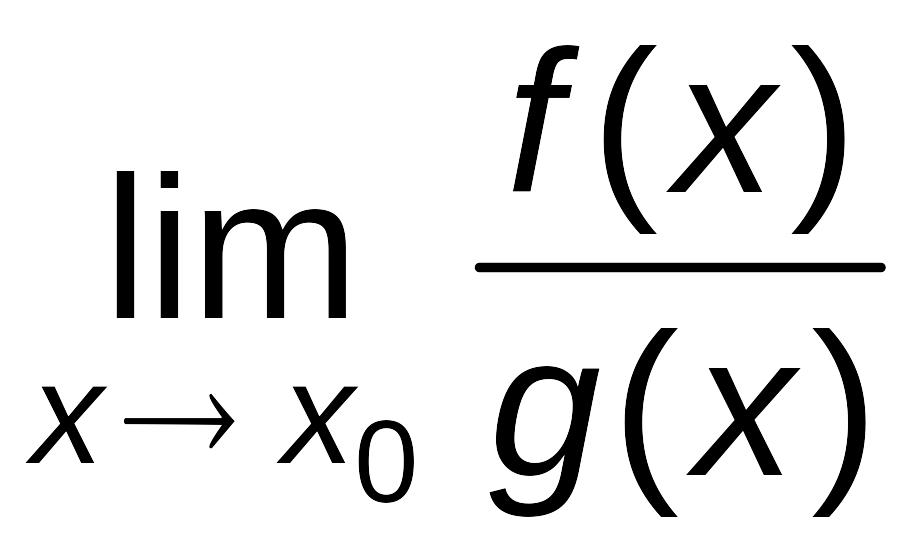
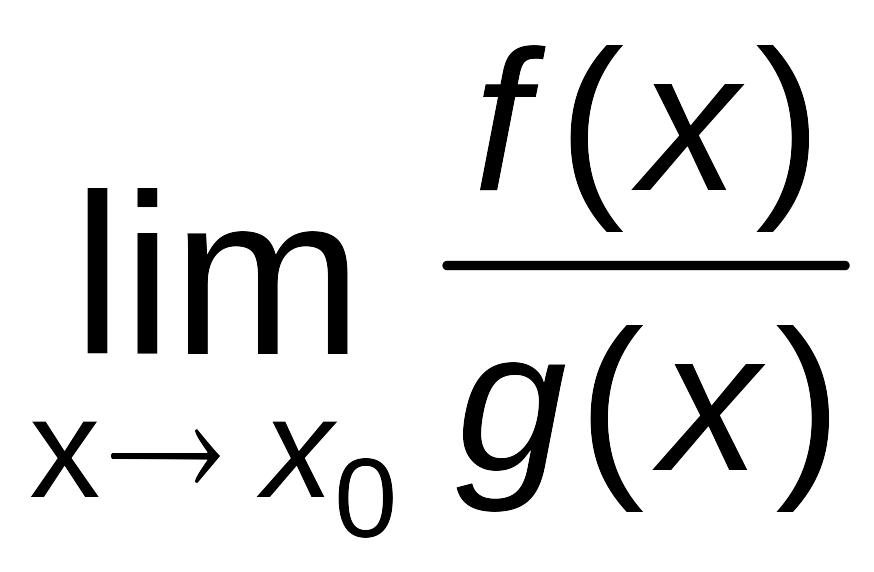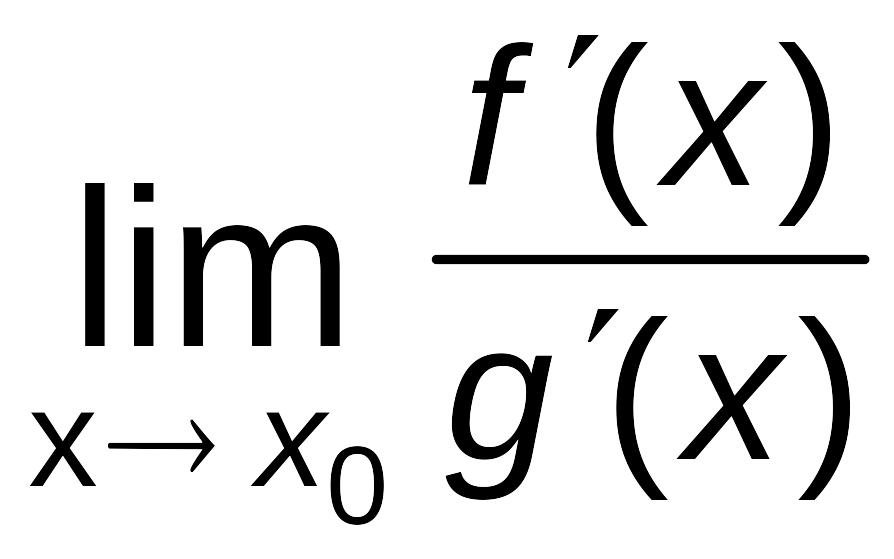Замечание 3. Предел отношения двух функций может существовать, в то время как предел отношения их производных не существует.
Например,
=1,
а
=
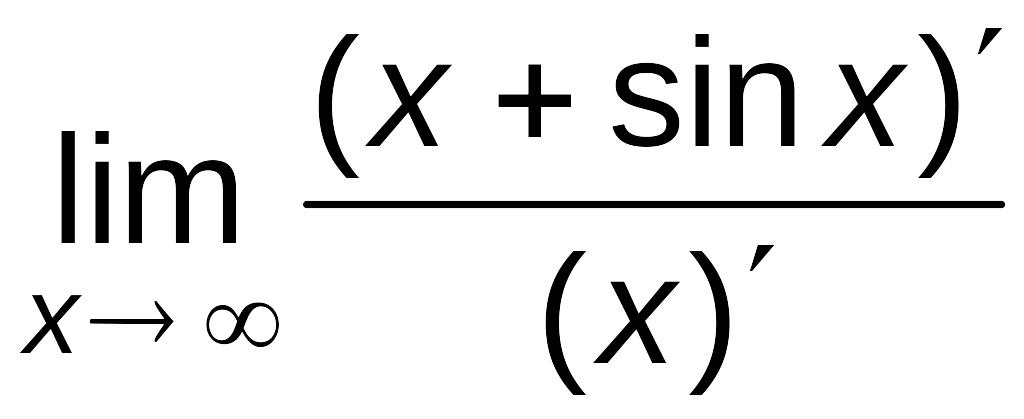– не существует, так как
не существует.
Замечание
4.
Если
при x
→
x0
(
)
является неопределенностью типа
или
,
и
,
g'(x)
удовлетворяют условиям теоремы Лопиталя,
то
=
=
.
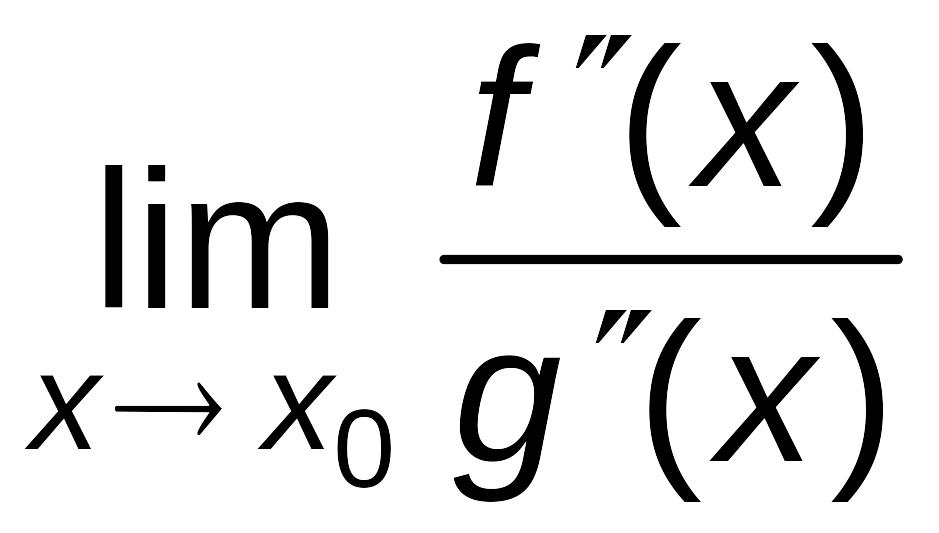Таким образом, для раскрытия неопределенностей типа или иногда приходиться применять правило Лопиталя несколько раз.
Пример
6.3.
Найти
.
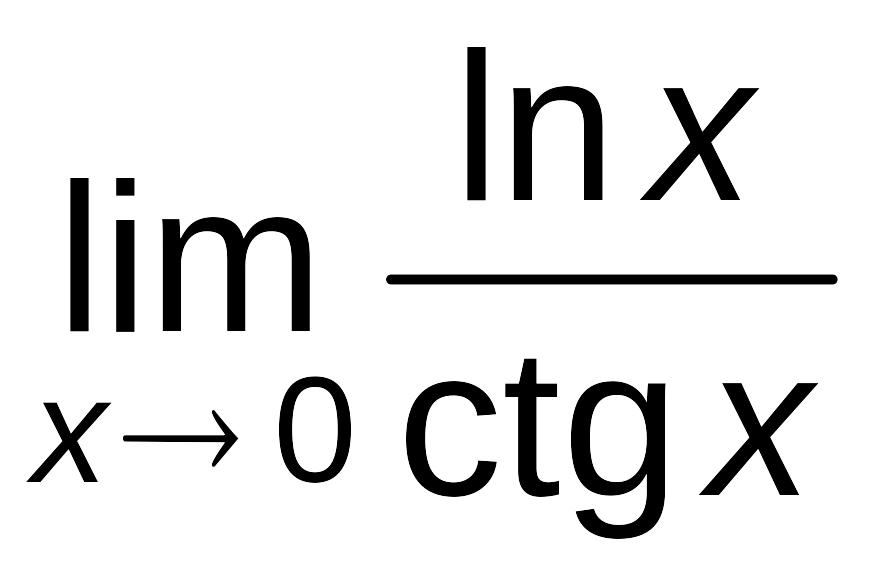Решение.
При
x
→
0 и x
>
0
,
,
следовательно, имеем отношение двух
бесконечно больших при x→0
и неопределенность типа
.
Вычислим:
=
–
=
–
=
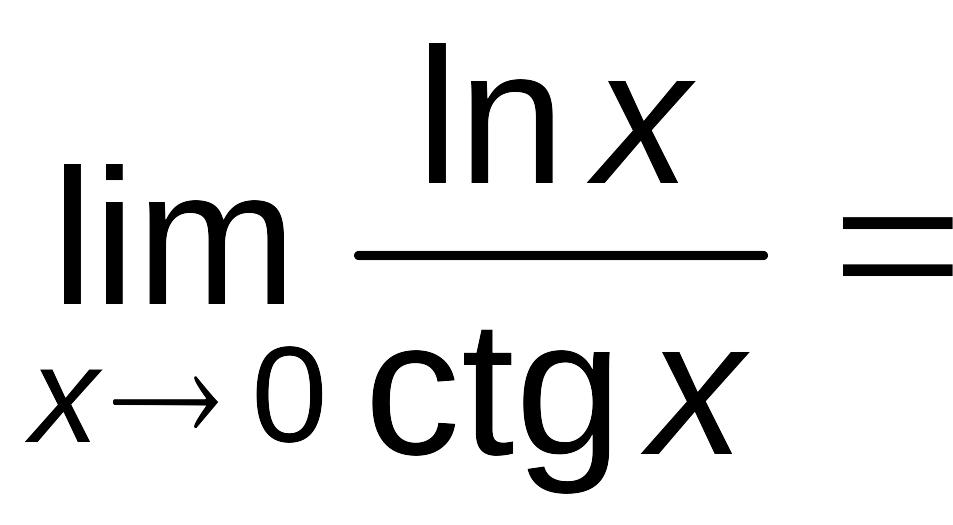
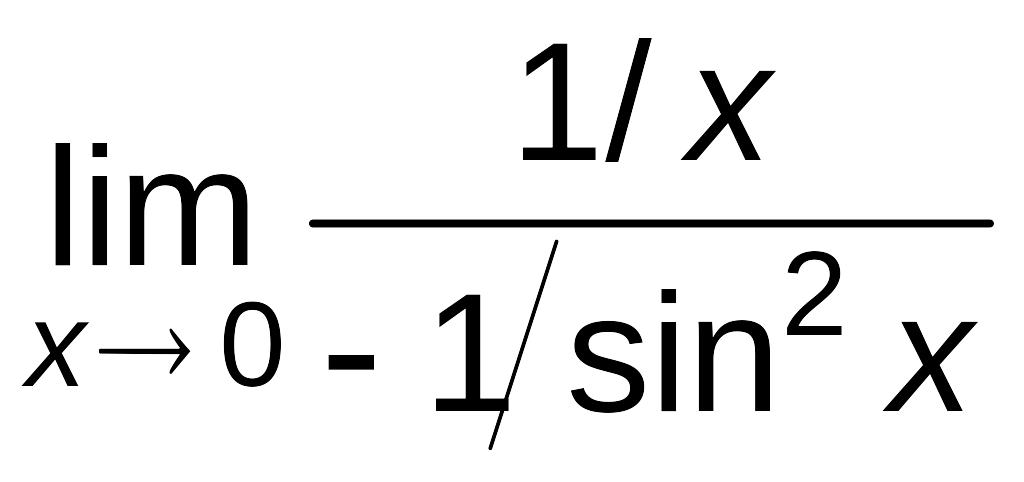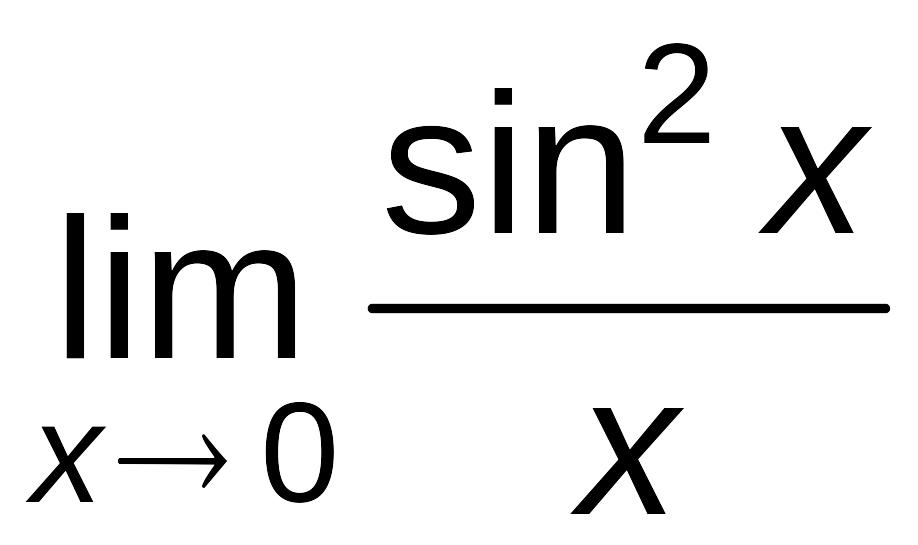0.
Пример
6.4.
Найти
.
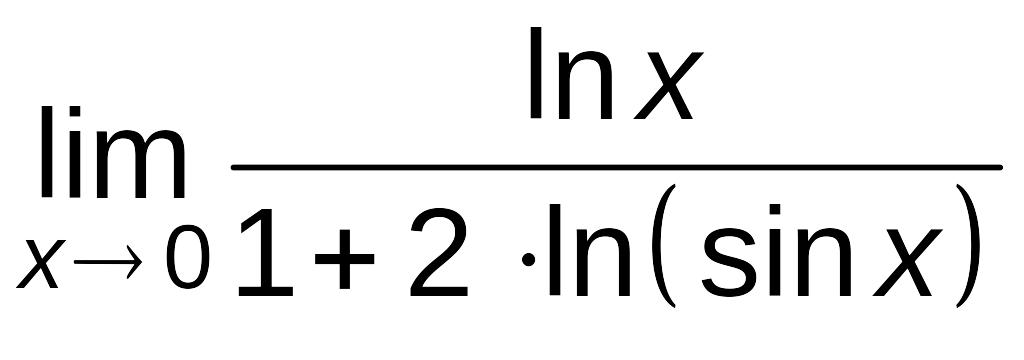Решение.
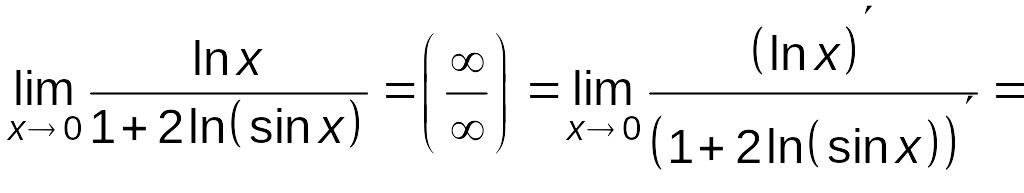
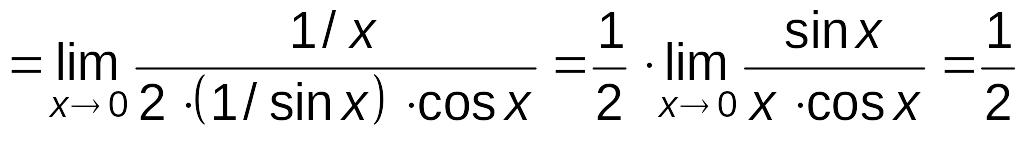
Пример
6.5.
Найти
.
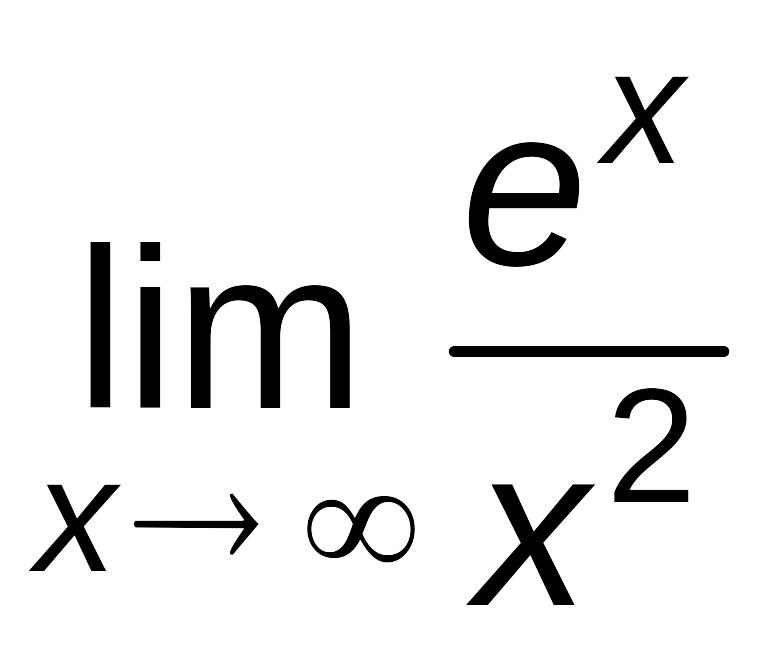Решение.
Имеем
неопределенность типа
.
Применяя теорему Лопиталя два раза,
получим:
=
=
=.
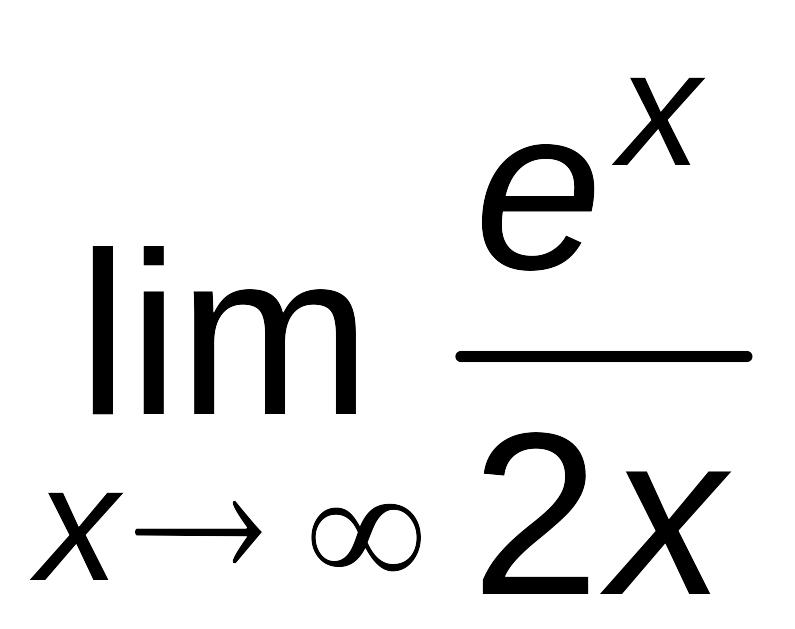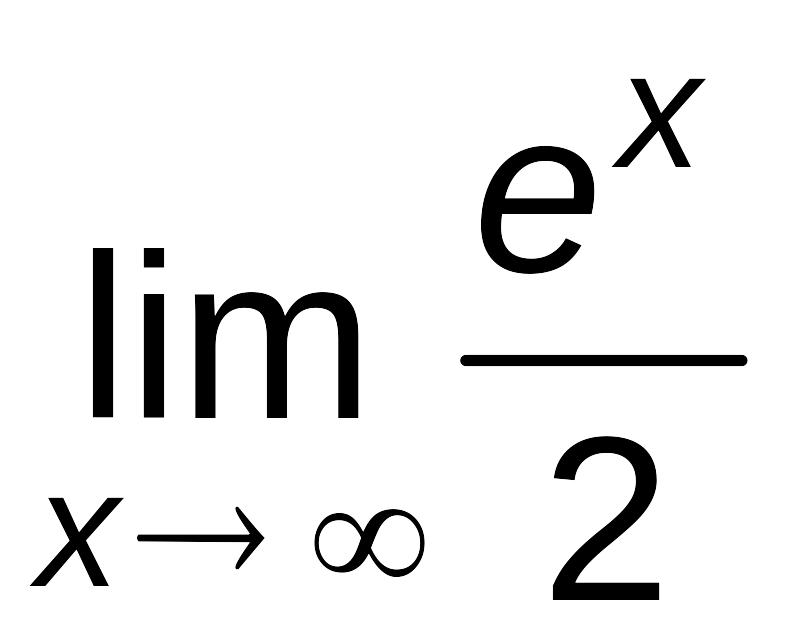Замечание
5.
Правило Лопиталя можно применять и к
неопределенностям другого вида, а именно
),
.
Неопределенности вида
можно свести к неопределенностям
и
.
Покажем это на примерах.
Пример
6.6.
Найти
.
Решение.
Так как , то имеем неопределенность типа (0·). Преобразуем ее к виду :
=
,
затем применим правило Лопиталя:
=
=
=
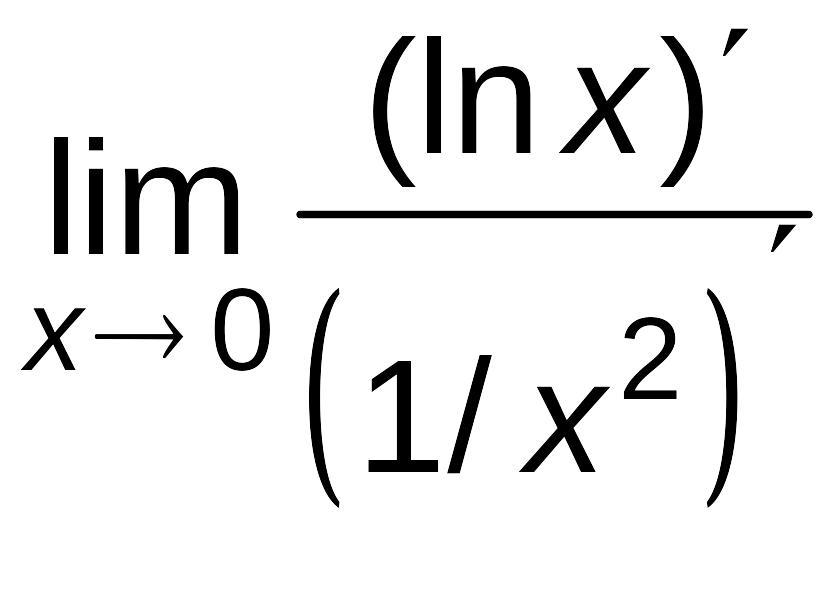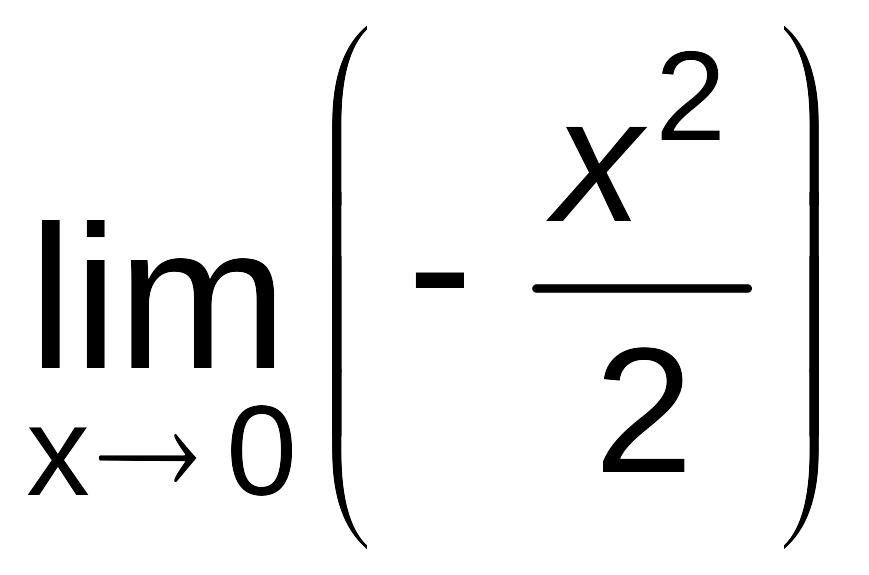=0.
Итак,
.
Пример
6.7.
Найти
Решение.
.
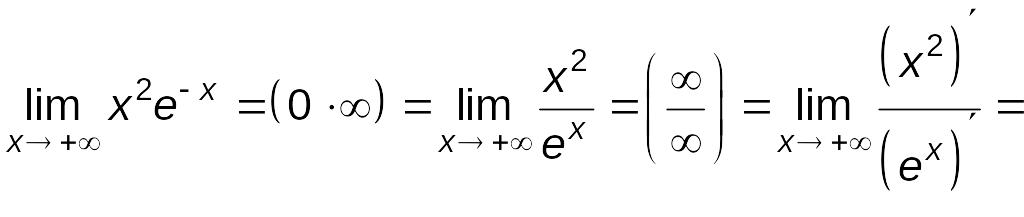
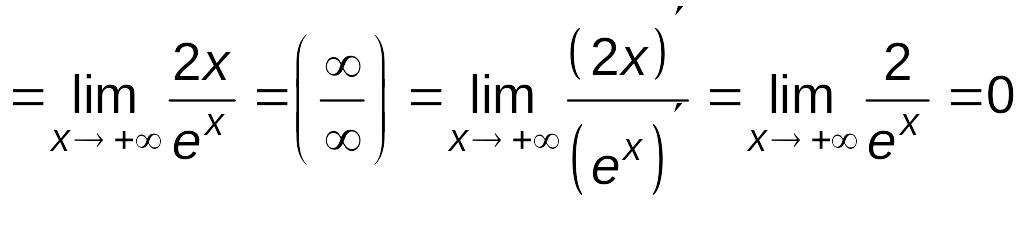Пример
6.8.
Найти
.
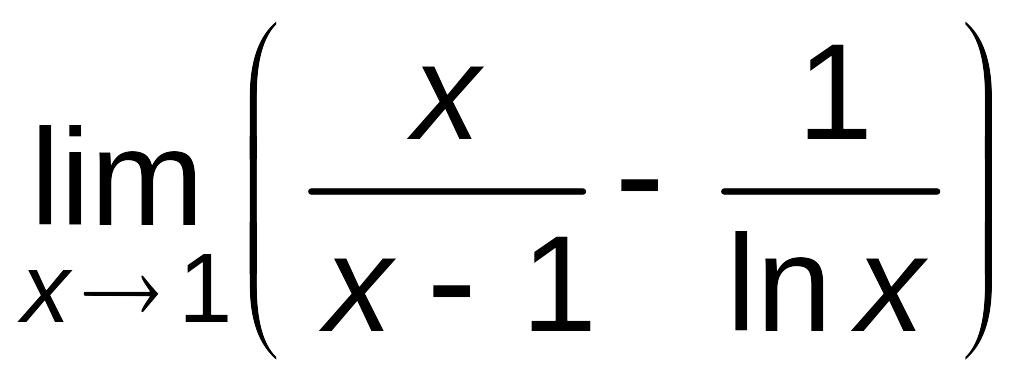Решение.
.
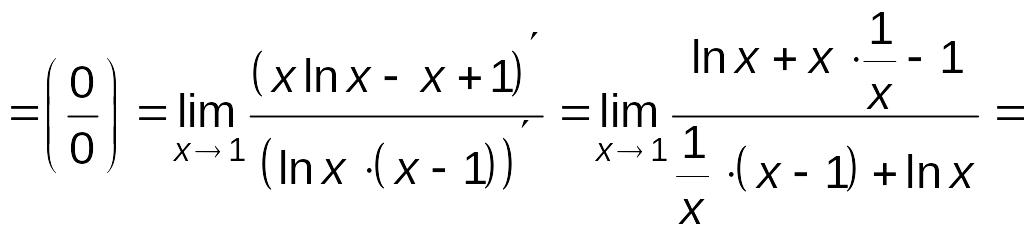
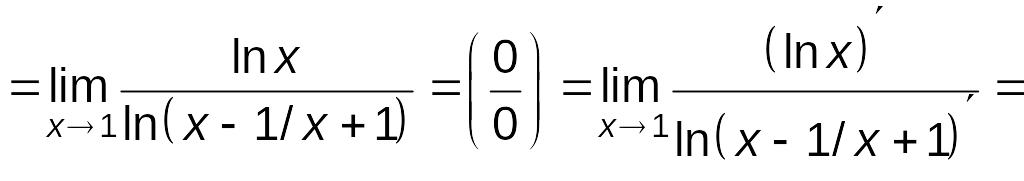
Рассмотрим
неопределенности вида (
),
.
Такие
неопределенности имеют место при
рассмотрении функций
,
если при
функция
стремится соответственно к 0, 1 и
,
– соответственно к 0,
и 0. Для раскрытия этих неопределенностей
функция предварительно логарифмируется
и, значит, сначала отыскивается предел
не заданной функции, а её логарифма, а
затем уже по пределу логарифма находится
предел функции (что допустимо вследствие
непрерывности логарифмической функции).
Рассмотрим это на примере.
Пример
6.9. Найти
.
Решение.
В
данном случае имеем неопределенность
типа
,
поэтому для раскрытия этой неопределенности
применим метод логарифмирования.
Пусть
.
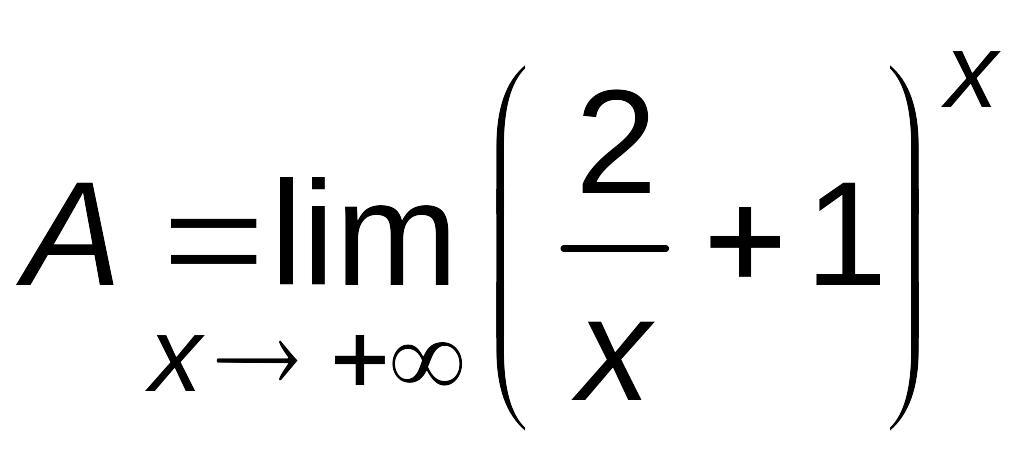Тогда с учетом того, что логарифмическая
функция непрерывна, имеем
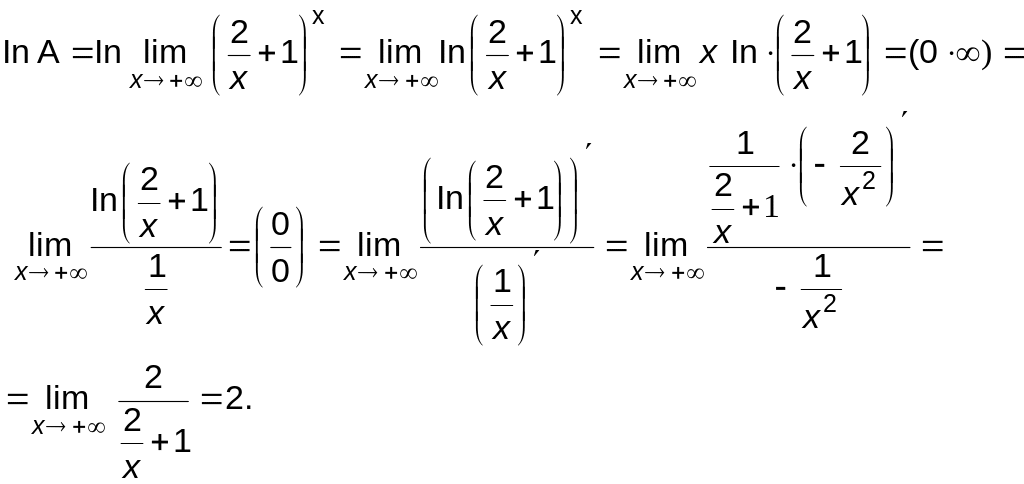
Так
как
,
то
