4.3. Дифференцирование функций, заданных параметрически

Рассмотрим задание линии на плоскости, при котором переменные x, y являются функциями третьей переменной t (называемой параметром):

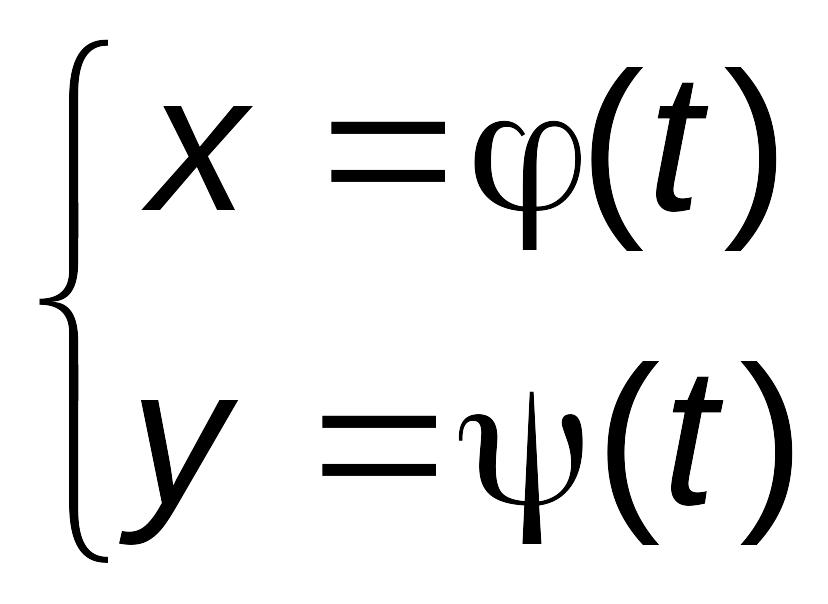. (4.3)

Каждому значению t из некоторого интервала соответствуют определенные значения x и y, а, следовательно, определенная точка M плоскости. Когда t пробегает все значения из заданного интервала, то точка M описывает некоторую линию L. Уравнения (4.3) называются параметрическими уравнениями линии L.

Если функция на некотором интервале изменения t имеет обратную функцию , то подставляя это выражение в уравнение , получим , которое задает y как функцию от x.

Пусть , имеют производные, причем . По правилу дифференцирования сложной функции . На основании правила дифференцирования обратной функции , имеем:

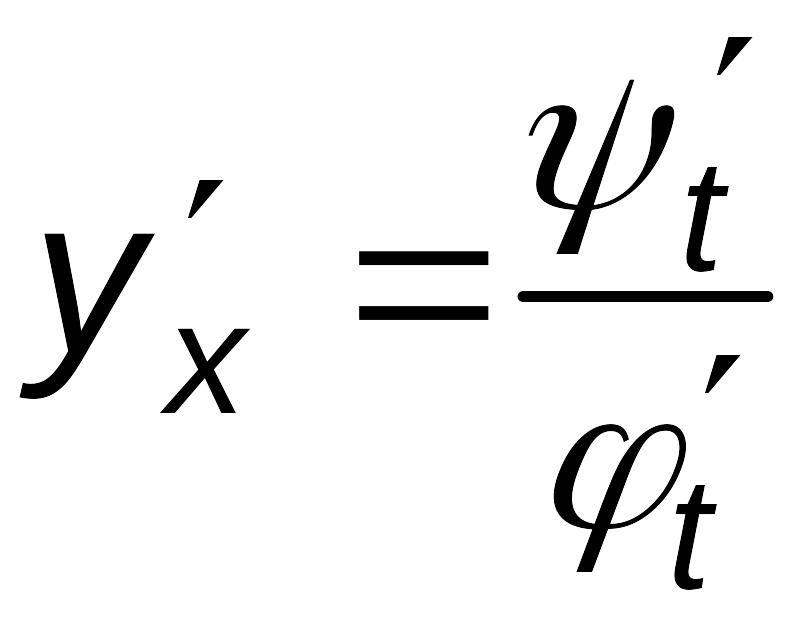. (4.4)

Полученная формула (4.4) позволяет находить производные для функций, заданных параметрически.

Пример 4.4. Пусть функция y, зависящая от x, задана параметрически:

.

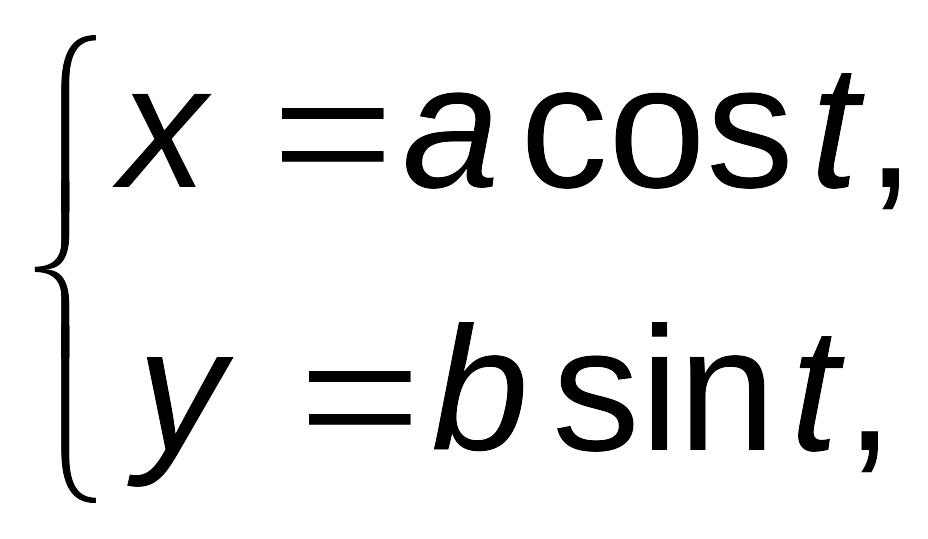
Найти .

Решение.

.

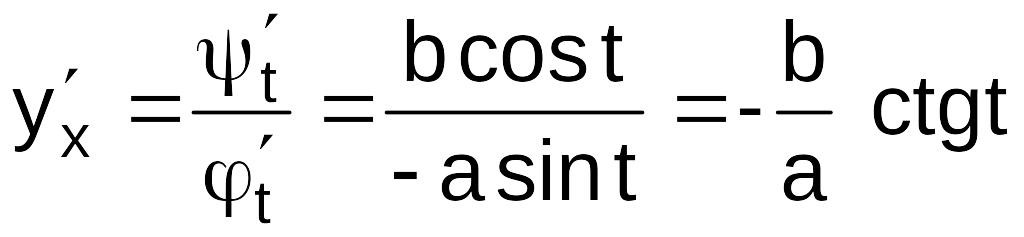Пример 4.5. Найти для функции, заданной параметрически:

.

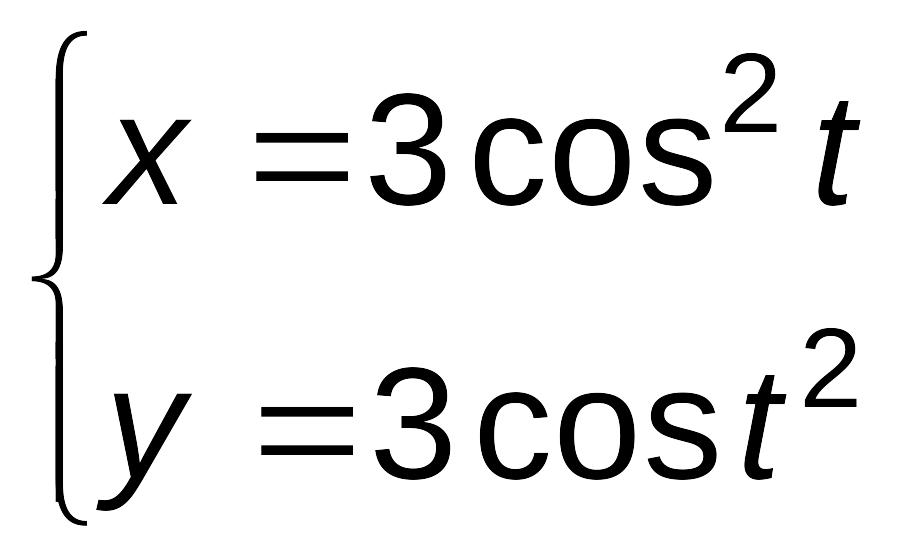Решение

;

;

.

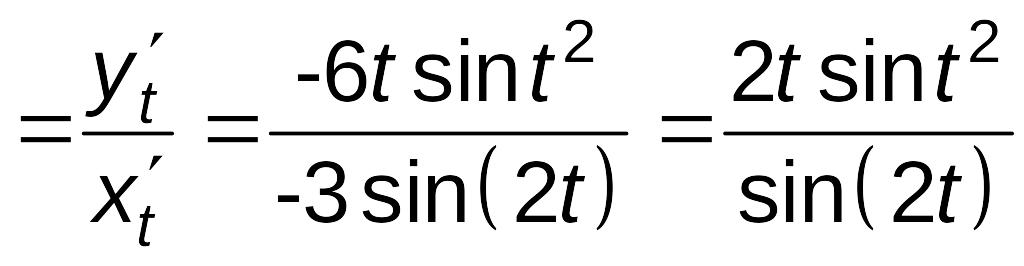4.4. Логарифмическое дифференцирование

Рассмотрим показательно-степенную функцию , где , u(x), v(x) – дифференцируемые функции.

Прологарифмируем равенство , получим: . По свойствам логарифмов для нашего равенства будем иметь . Дифференцируем обе части полученного равенства как неявную функцию. В дальнейших вычислениях для удобства переменную x будем не указывать, но помнить, что y – функция от x:

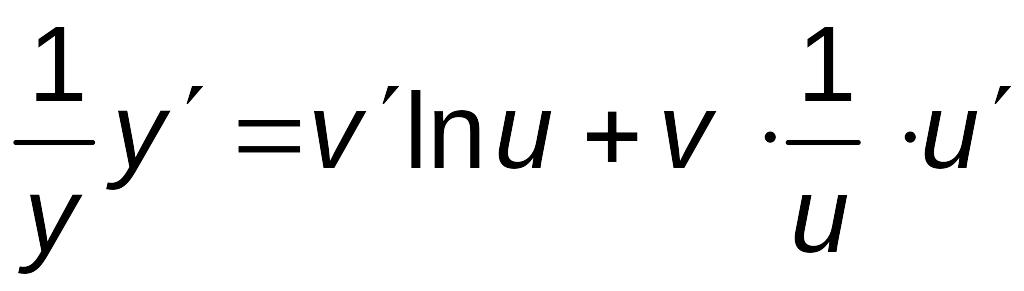, откуда .

Подставляя сюда , имеем:

.

Этот прием нахождения производной называется логарифмическим дифференцированием.

Пример 4.6. Найти производную функции .

Решение.

Прологарифмируем обе части равенства . Тогда

. Используя свойство логарифмов получим . Найдем производные от обеих частей полученного равенства, приравнивая их:

.

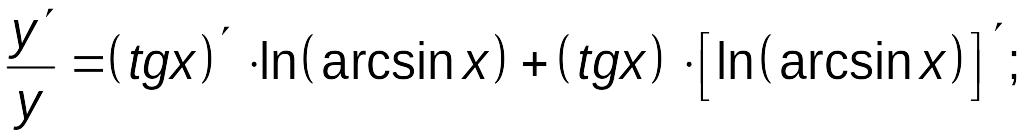
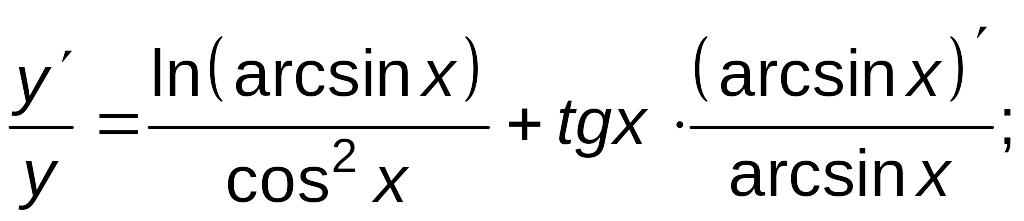
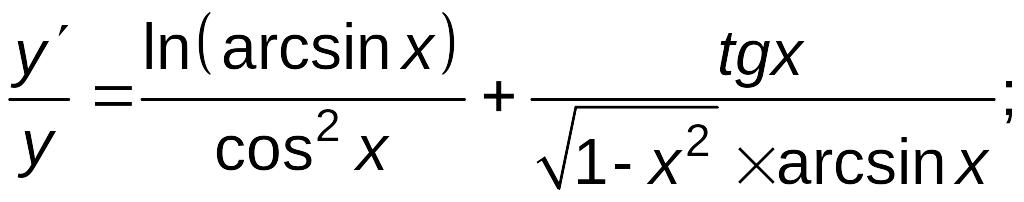Учитывая, что , имеем:

.

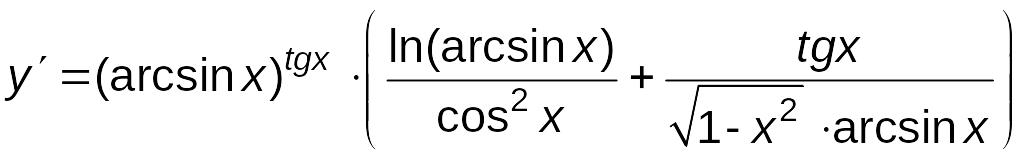Пример 4.7. Найти производную функции , (x > 0).

Решение.

Прологарифмировав обе части заданной функции получим . Воспользуемся свойством логарифмов . Дифференцируя полученное равенство по будем иметь:

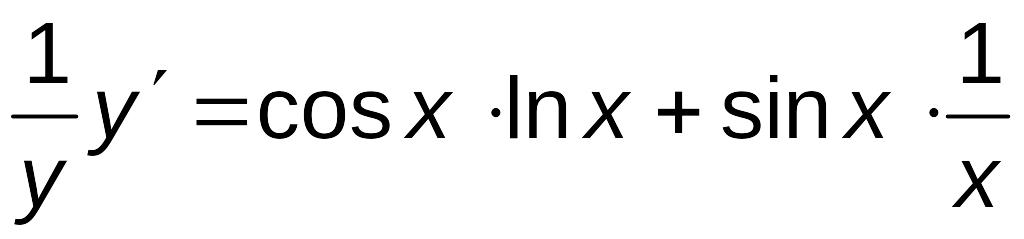, откуда

или .

5. Производные высших порядков

5.1. Понятие производной высшего порядка

Пусть функция определена и дифференцируема на некотором промежутке X, тогда ее производная также является функцией от x на этом промежутке. Если имеет производную на промежутке X, то эта производная называется производной второго порядка функции y = f(x) и обозначается: y'' или .

Итак,

Производная от производной второго порядка называется производной третьего порядка и обозначается: y''' или .

Вообще, производной n-го порядка называется производная от производной -го порядка и обозначается: y⁽ⁿ⁾ или f ⁽ⁿ⁾(x) или . Итак,

f ⁽ⁿ⁾(x) = (f ^(n-1)(x))'.

Производные y'', y''', ... называются производными высших порядков.

Пример 5.1. . Найти и .

Решение.

= = ,

= – ,

= = ,

= = = .

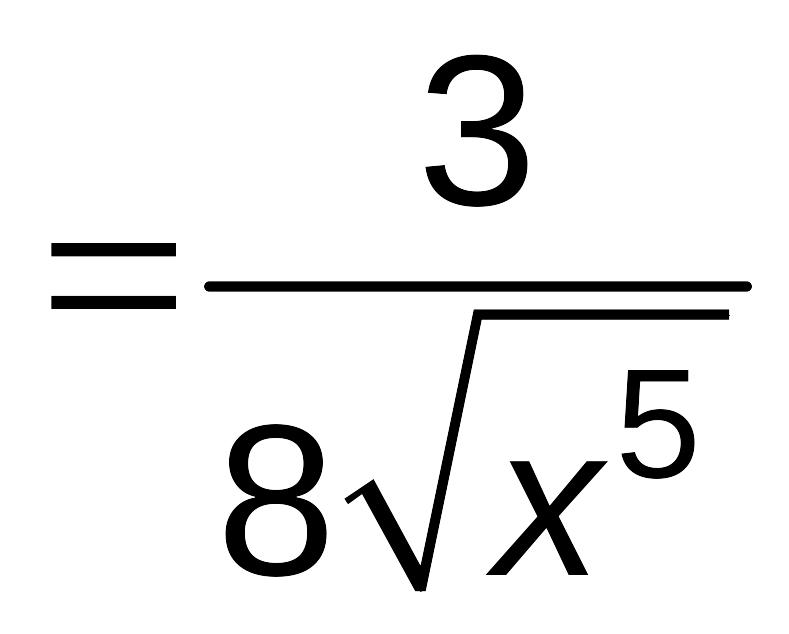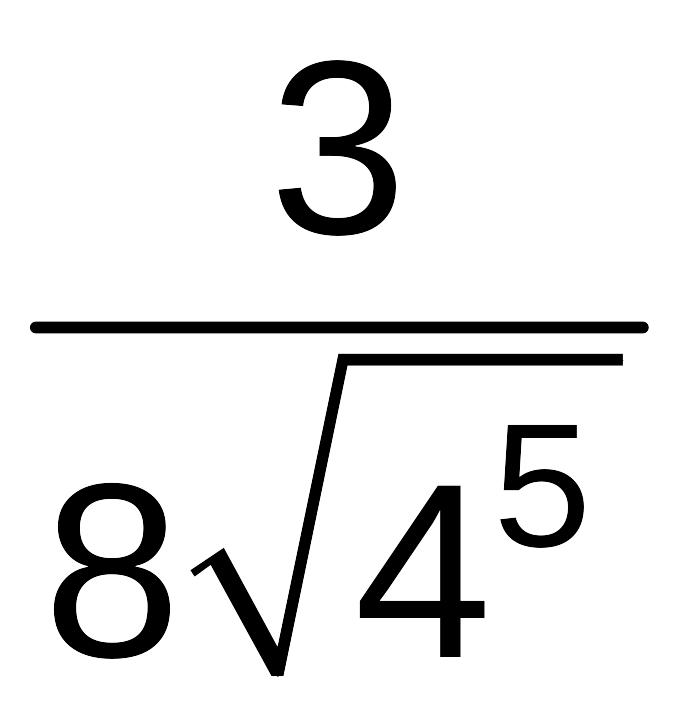Пример 5.2. Найти производную n-го порядка для функции .

Решение.

,

,

.

По аналогии находим: .