3. Дифференциал функции
Пусть
функция в точке x0
имеет производную. По определению
производной (п.1.1)
,
поэтому по свойствам предела можно
записать
,
где
–
бесконечно малая при
.
Отсюда
.
(3.1)
При
второе слагаемое в равенстве (3.1) является
бесконечно малой высшего порядка, по
сравнению с
:
,
поэтому
и
– эквивалентные бесконечно малые (при
(x0)
0).
Таким
образом, приращение функции
состоит из двух слагаемых, первое из
которых
является главной
частью
приращения
,
линейной относительно
(при
).
Дифференциалом
функции
в точке
называется главная часть приращения
функции в точке
и обозначается:
или
.
Следовательно,
.
(3.2)
Отметим, в частности, что
,
т. е. дифференциал независимого переменного равен его приращению.
Это дает возможность представить формулу (3.2) в виде
и с другой стороны, записать производную в виде отношения дифференциалов:
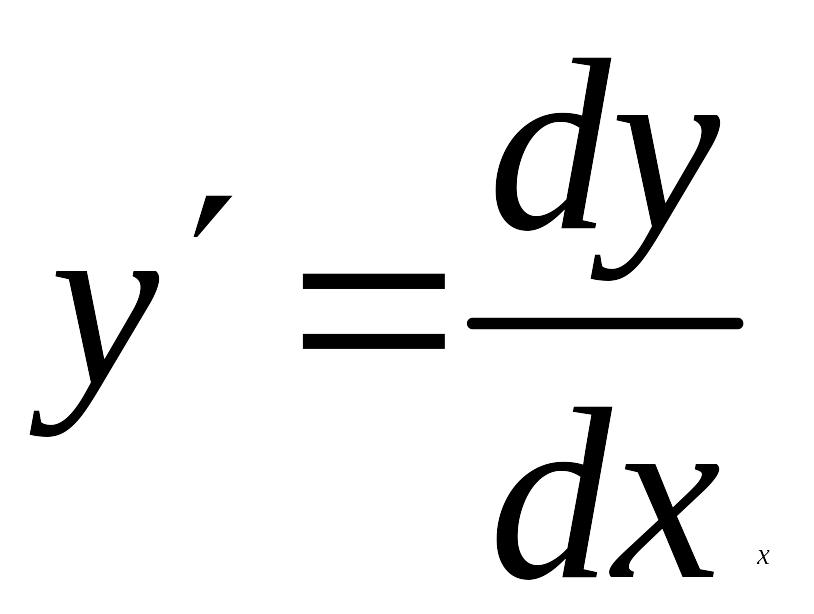или,
что
.
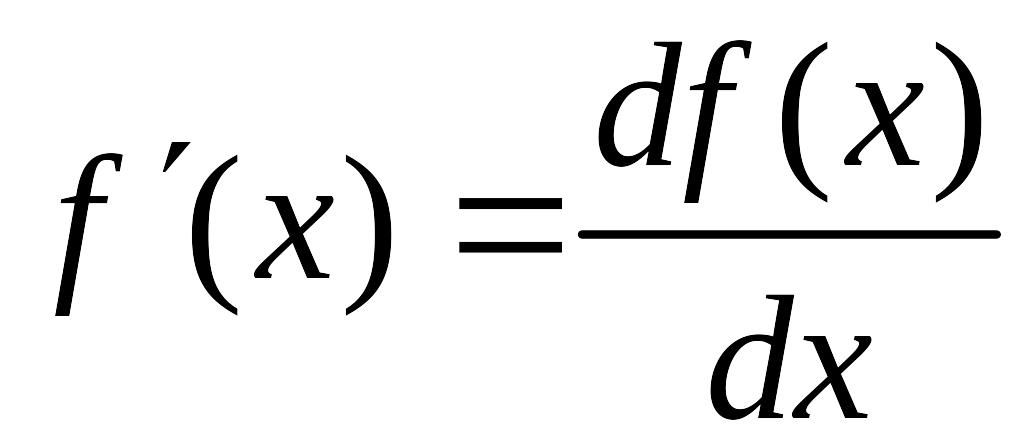Пример
3.1.
Найти дифференциал и приращение функции
при: 1) произвольных
и
;
2)
,
.
Решение.
1)
,
.
2)
Если
,
,
то
;
.
Запишем равенство (3.1) в виде:
.
(3.3)
Приращение
отличается от дифференциала
на бесконечно малую высшего порядка,
по сравнению с
,
поэтому в приближенных вычислениях
пользуются приближенным равенством
,
если
достаточно мало.
Учитывая,
что
,
получаем приближенную формулу:
.
(3.4)
Пример
3.2.
Вычислить приближенно
.
Решение.
Рассмотрим:
,
,
.
Тогда
.
,
.
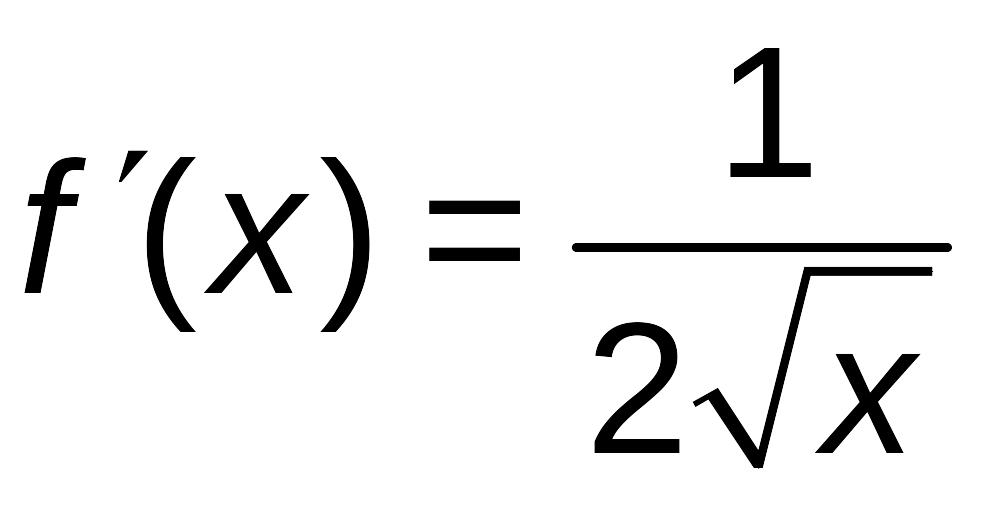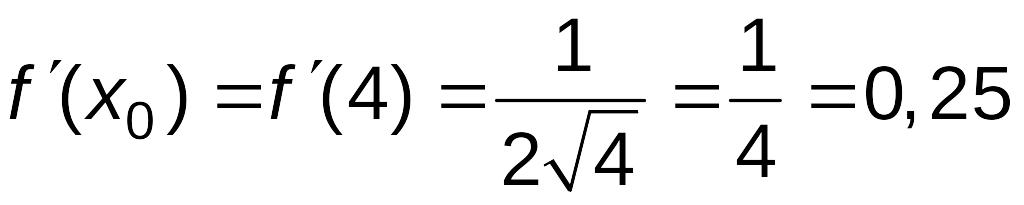
Используя формулу (3.4), получим:
.
4. Дифференцирование обратной функции, функций заданных неявно, параметрически. Логарифмическое дифференцирование
4.1. Дифференцирование обратной функции
Введем правило для нахождения производной обратной функции.
Теорема.
Пусть функция
определена на промежутке Х,
непрерывна, монотонна (возрастает или
убывает) и дифференцируема на Х.
Если ее производная
в точке
не равна нулю, то обратная
функция
имеет производную
в точке
,
причем
.
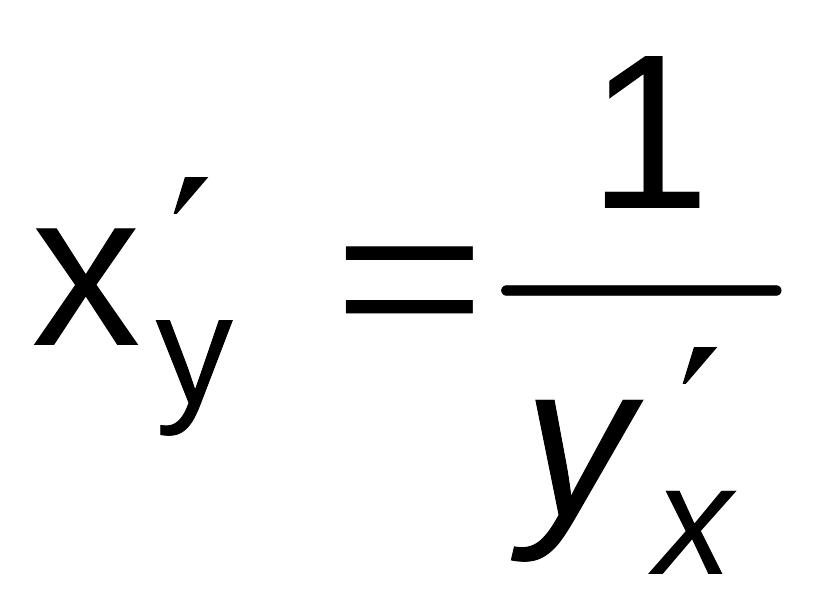(4.1)
Доказательство.
Функция
определена, непрерывна и монотонна на
промежутке Х,
тогда она имеет обратную функцию
,
определенную, непрерывную и монотонную
на промежутке Y.
Если
значение аргумента
получает приращение
,
отличное от нуля, то в силу монотонности
функции
функция
получает приращение
и
.
В силу непрерывности функции
:
.
Следовательно,
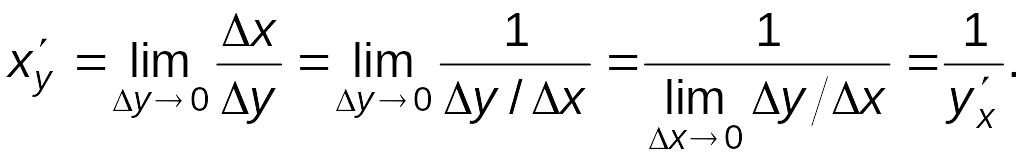
Итак,
Теорема доказана.
Пример
4.1.
Если
,
,
то функции
,
являются взаимно обратными, причем
.
Если
(при этом
),
то
,
поэтому
.
По
формуле (4.1) имеем:
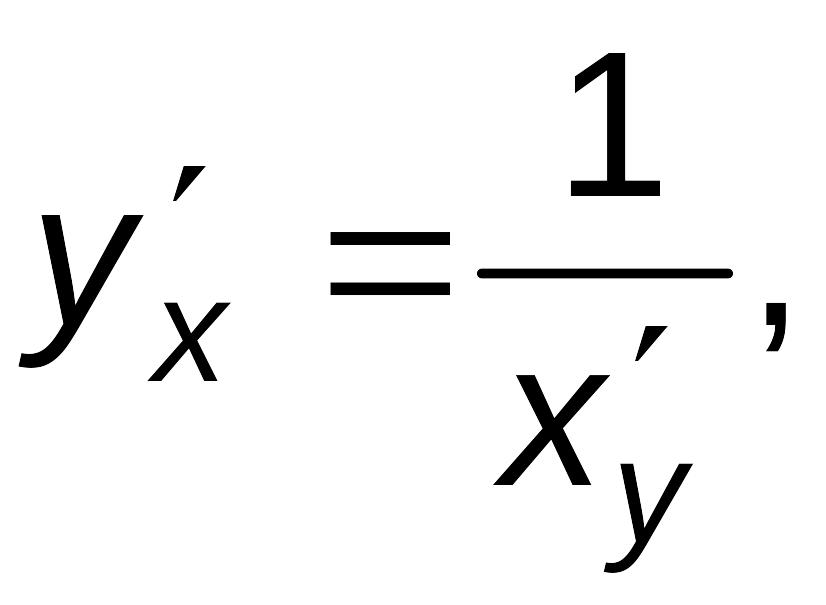тогда
(
).
4.2. Дифференцирование функций, заданных неявно
Не
всегда функция бывает представлена в
виде
.
Например, уравнение
задает функцию y,
которую можно из этого уравнения выразить
через
:
.
Пусть
переменные
связаны между собой некоторым уравнением
,
(4.2)
причем y является функцией от x. Тогда говорят, что функция y задана неявно уравнением (4.2).
Не
всегда функции, заданные неявно могут
быть выражены явно через элементарные
функции. Так, из уравнения
,
которое неявно задает функцию y,
нельзя выразить y
явно через элементарные функции.
Для того чтобы найти производную y' для функции, заданной неявно уравнением (4.2) надо найти производные по x от обеих частей этого уравнения, помня, что y – функция от x и приравнять эти производные. Из полученного уравнения найти y'.
Пример
4.2.
Найти производную функции, заданной
неявно уравнением
.
Решение.
.
.
Отсюда
.
Пример
4.3.
Найти
,
если переменные
и
связаны соотношением
.
Решение.
Явно выразить одну из переменных через другую невозможно, поэтому находим производные левой и правой частей данного равенства и приравниваем их:
.
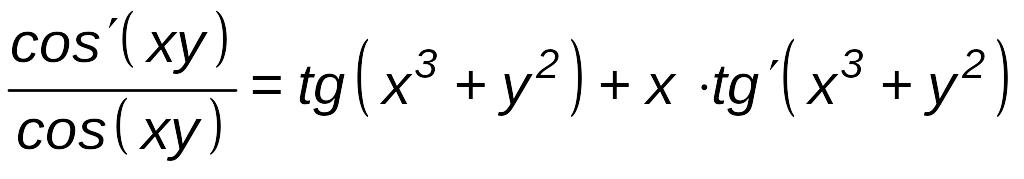Далее имеем:
;
.
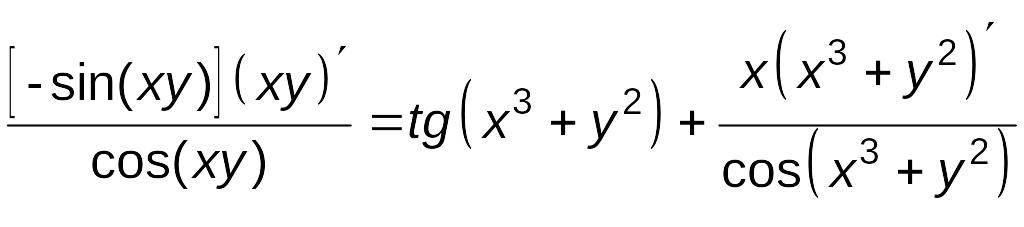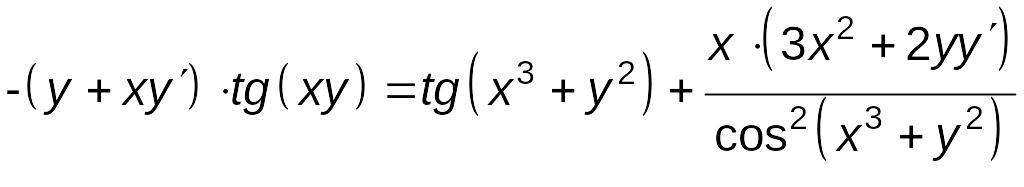Перенося слагаемые, содержащие , в одну часть равенства, вынося за скобку, а остальные слагаемые – в другую, и деля на коэффициент при , получаем:
.
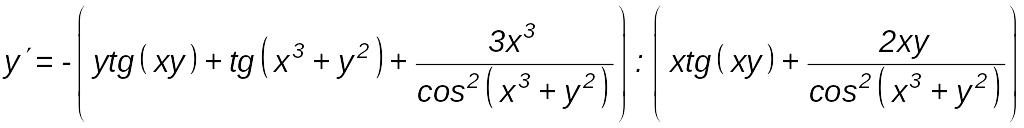