Лабораторна робота №6.

Тема: Наближене обчислення визначених інтегралів.

Мета: Навчитись обчислювати визначені інтеграли за допомогою чисельних методів.

Теоретичні відомості

Якщо для неперервної на проміжку [а; b] фукнкції відома первісна , то визначений інтеграл

(6.1)

можна обчислити за допомогою формули Ньютона-Лейбніца:

.

Проте в багатьох випадках первісна не виражається через елементарні функції або її знаходження вимагає проведення громіздких обчислень. Крім того, на практиці часто доводиться мати справу з функціями, що задані на відрізку [а; b] таблично чи графічно. В таких випадках для обчислення визначеного інтеграла застосовують наближені методи.

Далі розглядаються найбільш уживані формули наближеного обчислення визначених інтегралів.

Формула прямокутників.

Нехай потрібно обчислити інтеграл (6.1). Проміжок інтегрування [а; b] розіб’ємо на n рівних частин точками

де

Тоді за означенням визначеного інтеграла маємо:

де - довжина і-го відрізка [x_i-1; x_i], - деяка точка цього відрізка .

При достатньо великому n за наближене значення визначеного інтеграла (6.1) можна прийняти інтегральну суму

(6.2)

У формулі (6.2) точки можна вибирати довільно. Найчастіше за беруть ліві або праві кінці проміжків , або середини цих проміжків. Якщо , матимемо так звану формулу лівих прямокутників

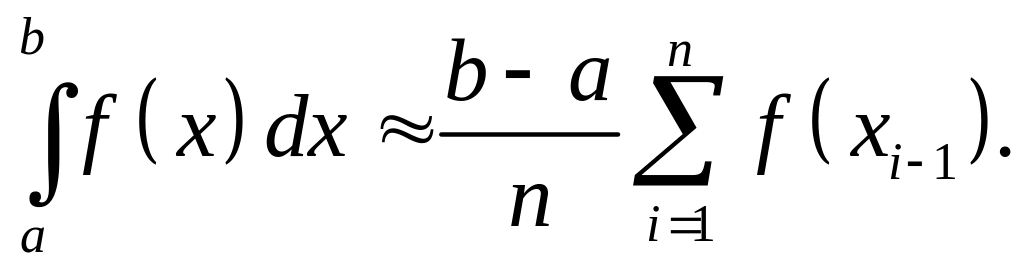(6.3)

Якщо ж , одержимо формулу правих прямокутників

(6.4)

Поклавши , матимемо формулу

(6.5)

яка називається формулою прямокутників. При заданому n формула (6.5) дає більш високу точність, ніж формули (6.3) і (6.4).

З теорії наближених методів обчислень відома оцінка абсолютної похибки формул прямокутників.

Якщо функція має на проміжку [а; b] неперервну похідну другого порядку, то

де - найбільше значення модуля другої похідної на [а; b].

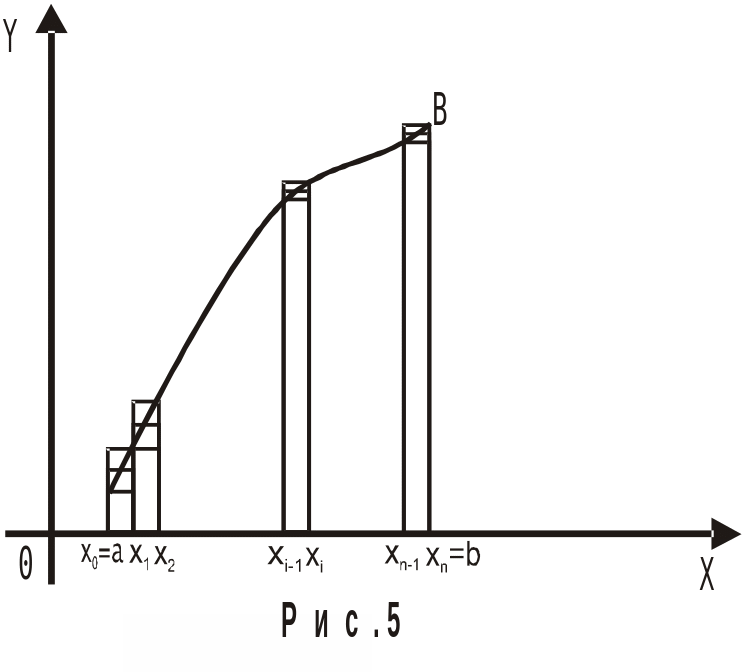
Для випадку невід’ємної функції ( на [а; b]) одержані формули мають просту геометричну інтерпретацію. Як відомо, інтеграл (6.1) дає в цьому випадку площу криволінійної трапеції aABb (рис.5). Праві частини формул (6.3) – (6.5) виражають площі ступінчастих фігур, складених з відповідних прямокутників.

Формула трапецій.

Загальний метод побудови формул чисельного інтегрування (квадратичних формул) полягає в наступному. Нехай потрібно обчислити наближено інтеграл (6.1). Тоді заміняють підінтегральну функцію на всьому відрізку [а; b] чи на його окремих частинах більш простою функцією , яка легко інтегрується точно і приймає в заданих (вибраних) точках ті ж значення, що й : . Зокрема, за функцію можна взяти інтерполяційний алгебраїчний многочлен чи іншу інтерполяційну функцію.

Розіб’ємо, як і в п. 6.1, відрізок [а; b] на n рівних частин і замінимо функцію на кожному проміжку лінійною інтерполяційною функцією, побудованою за двома вузлами та :

Тоді матимемо

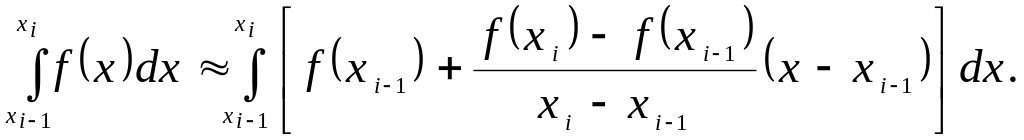
виконавши інтегрування в правій частині цієї рівності, дістанемо

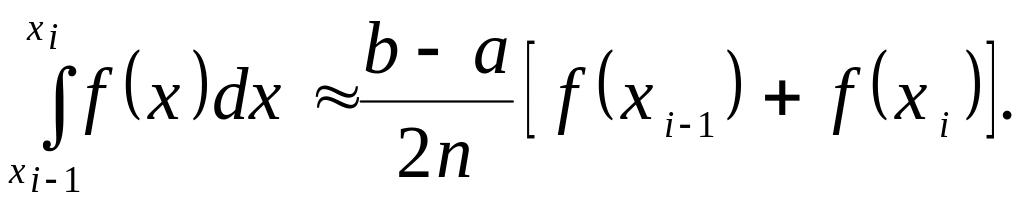
Об’єднуючи інтеграли по всіх відрізках в один, матимемо наближену формулу:

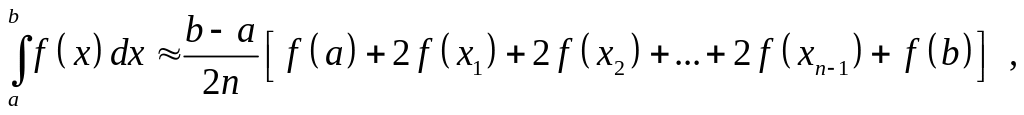(6.6)

яку називають формулою трапецій.

Т ака назва пояснюється тим, що для замість площі криволінійної трапеції (рис.6) ми беремо площу звичайної трапеції.

Оцінка абсолютної похибки формули трапеції (6.6) має вигляд

, де, як і раніше, .

Формула Сімпсона.

Для виводу цієї квадратурної формули розіб’ємо відрізок [а; b] на парне число n = 2m рівних частин точками

де На відрізку замінимо функцію квадратичною інтерполяційною функцією (параболою) , побудованою за трьома точками Коефіцієнти рівняння параболи знаходяться як розв’язки системи рівнянь

Можна показати, що має місце рівність

Тепер для відрізків маємо

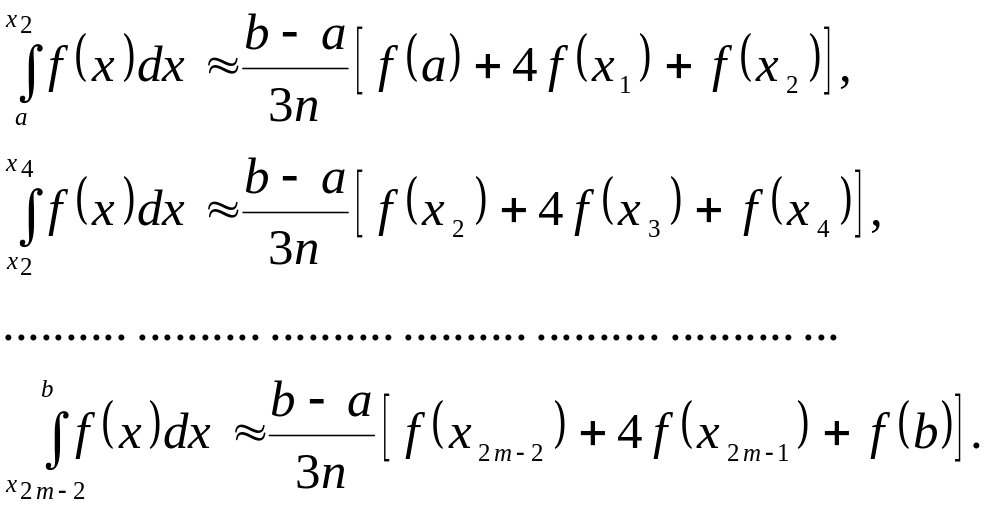
Додавши ліві і праві частини цих рівностей, одержимо наближену формулу

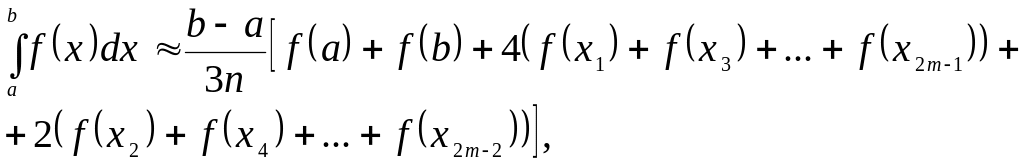
яка називається формулою Сімпсона (або формулою парабол).

Встановлено, що коли функція має на проміжку [а; b] неперервну похідну четвертого порядку, то абсолютна похибка формули Сімпсона оцінюється так:

де

Як бачимо, точність формули Сімпсона значно вища за точність формул прямокутників чи формули трапецій.

Крім розглянутих формул чисельного інтегрування, за тією ж схемою побудовано цілий ряд інших квадратурних формул (формули Гаусса, Ерміта, Чебишева).

Завдання: обчислити визначений інтеграл 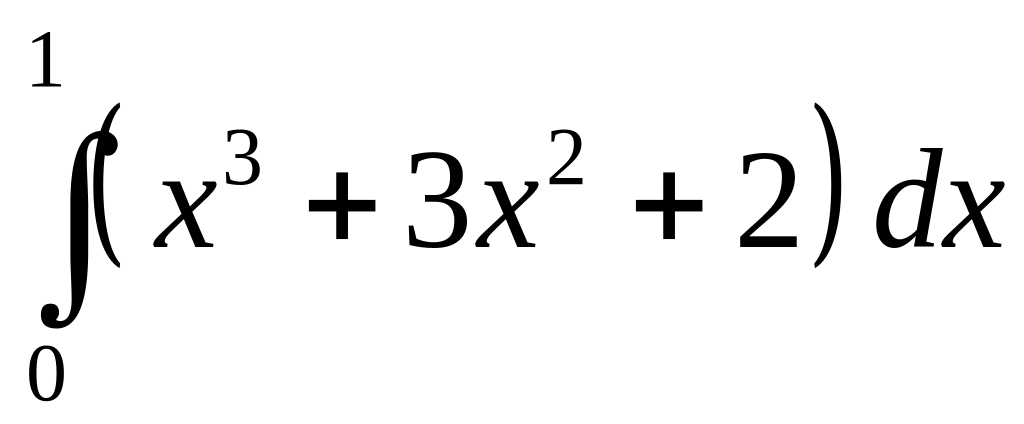, розбивши проміжок інтегрування на 100 частинних відрізків. Визначте абсолютну та відносну похибку кожного з методів. Зробіть висновки.

Метод прямокутників