Лабораторна робота №5.

Тема: Наближене розв’язування систем лінійних алгебраїчних рівнянь (метод простої ітерації).

Мета: Набути вмінь та навичок з отримання наближених розв’язків систем лінійних алгебраїчних рівнянь за допомогою ітеративних методів на прикладі методу Гауса – Зейделя, а також навчитись оцінювати похибку одержаного розв’язку та отримувати розв’язок системи з будь-якою наперед заданою точністю.

Теоретичні відомості

Розв’язання систем лінійних алгебраїчних рівнянь є однією з поширених задач прикладної математики. Розрізняють прямі (точні), ітеративні (наближені) та комбіновані методи розв’язування цієї задачі. Для великих систем доцільно користуватися наближеними (ітеративними) методами, оскільки об’єм обчислень значно зростає і, крім того, розв’язки, знайдені за згаданими прямими методами, можуть виявитися нестійкими (чисельний метод називається стійким, якщо результати неперервно залежать від вхідних даних задачі та похибка округлень, зв’язана з реалізацією методу на ПЕОМ, залишається обмеженою при згаданих межах змінювання параметрів методу). В результаті застосування ітеративних методів приходимо до послідовності наближених розв’язків, збіжної до шуканого (точного) розв’язку вихідної задачі. При цьому початковими даними для кожної наступної процедури наближення слугують результати попередніх процедур.

Нехай маємо систему n лінійних алгебраїчних рівнянь з n невідомими:

(5.1)

або в матричній формі

(5.1*)

Припустимо, що система (5.1) має єдиний розв’язок , тобто її визначник .

Нехай систему (6.1) будь-яким чином зведено до вигляду

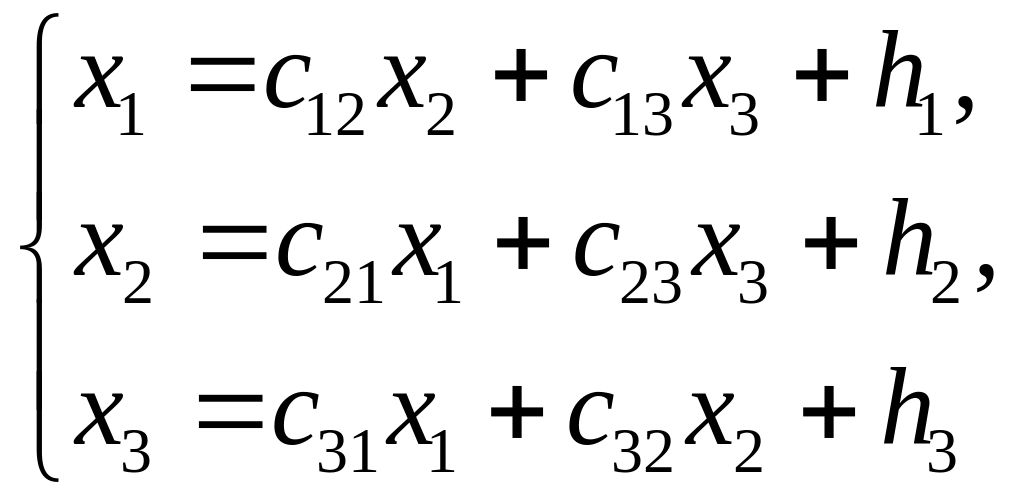(5.2)

де ,

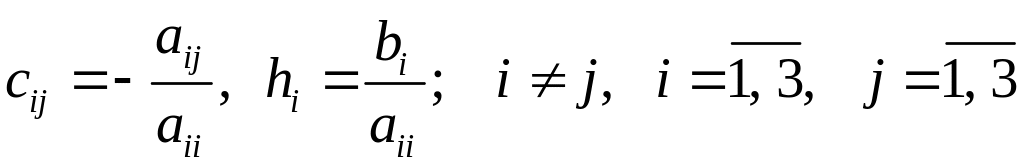що називається зведеною системою. Процес ітерації будується для зведеної системи (6.2) за формулами

(5.3)

де

; – нульове наближення до точного розв’язку .

Якщо послідовність наближень збігається до деякого граничного вектора , то він і буде розв’язком системи (5.1).

Теорема (достатня умова збіжності процесу ітерацій).

Послідовність в методі простої ітерації є збіжною, якщо для елементів матриці виконується одна з наступних нерівностей:

(5.4)

(5.5)

Якщо визначник , то систему (5.1) завжди можна (але це не завжди просто) перетворити до зведеної (5.3) з виконаною достатньою умовою збіжності (5.4) або (5.5).

Цей перехід легко здійснити, якщо елементи матриці вихідної системи (5.1) задовольняють слідуючим умовам:

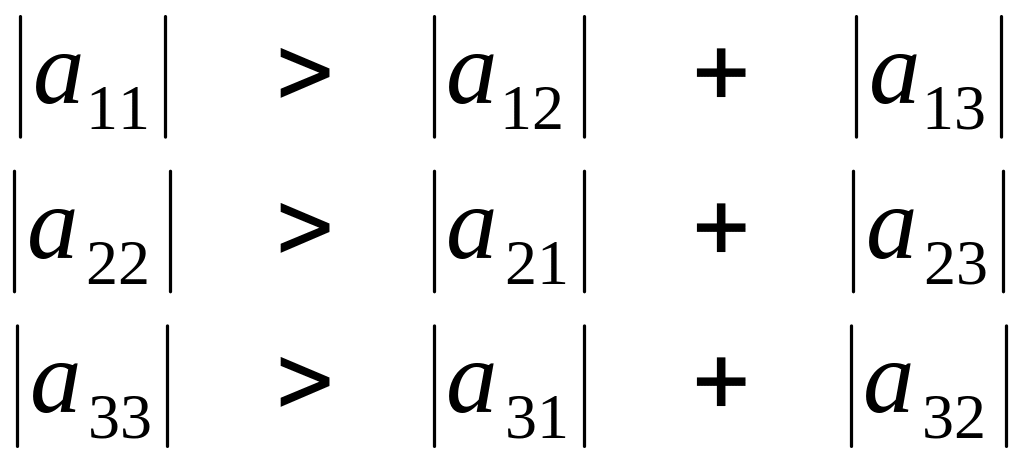(5.6)

Для побудови зведеної системи, при виконанні умови (6.6), необхідно кожне рівняння (5.1) розв’язати відносно змінних при діагональних елементах матриці . При цьому одержимо систему, для якої виконується необхідна умова збіжності (5.4).

Оцінка похибки -го наближення (тобто оцінка різниці ) за методом простої ітерації, визначається за формулою:

(5.7)

Для отримання результату з певною заданою точністю  ( – як завгодно мале додатне число) потрібно після кожної ітерації перевіряти виконання умови

(5.8)

Якщо умова (5.8) виконується для певного , то процес ітерації закінчено. Якщо ж ні, слід шукати наступне наближення за формулою (5.3).

Завдання: знайти розв’язок наведеної нижче системи лінійних алгебраїчних рівнянь з точністю за допомогою методу простої ітерації.

1. У робочому зошиті запишіть наведену вище систему рівнянь. Перевірте, чи виконується для кожного з рівнянь достатня умова збіжності процесу ітерації (модуль одного з коефіцієнтів при невідомих у рівнянні має бути більшим за суму модулів інших коефіцієнтів).

2. Побудуйте еквівалентну їй систему рівнянь (поміняйте рівняння у системі місцями таким чином, щоб рівняння з найбільшим по модулю коефіцієнтом при першій змінній стояло у новій системі на першому місці, з найбільшим по модулю коефіцієнтом при другій змінній – на другому місці тощо).

3. Запишіть відповідну даній зведену систему рівнянь, виразивши для цього з кожного рівняння змінну, яка має найбільший по модулю коефіцієнт. При цьому система набуде вигляду (6.2), де – нульове наближення до точного розв’язку . Для даної системи рівнянь значення нульового наближення таке:

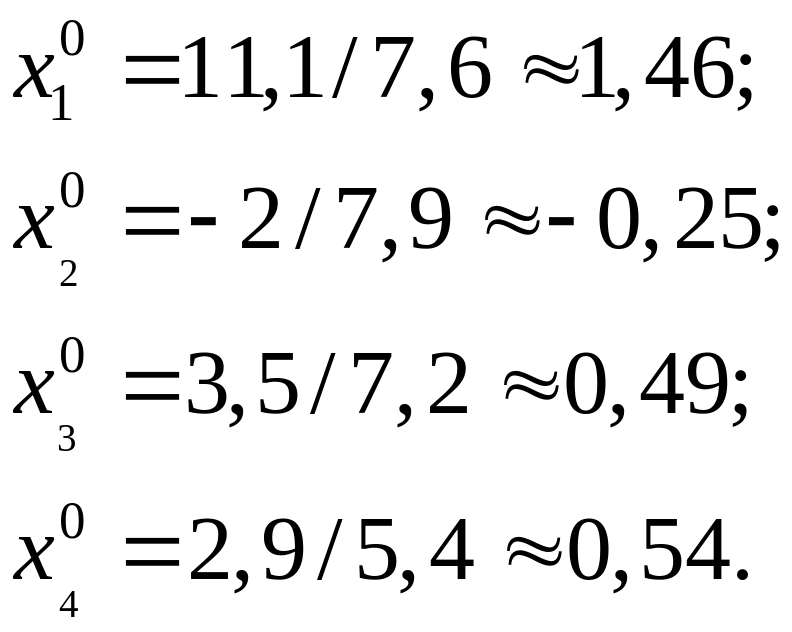
4. Наступні наближення до точного розв’язку шукатимемо за формулами (6.3) за допомогою комп’ютера, використовуючи програму Microsoft Excel.

5. Запустіть програму Microsoft Excel, збережіть файл у робочу папку під назвою Метод простої ітерації.xls

6. Введіть з клавіатури у комірки робочого аркуша коефіцієнти при невідомих у системі рівнянь, яка була отримана в п.2, у вигляді:

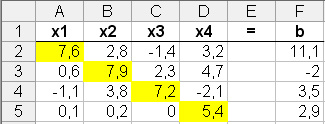
7. Знайдіть нульове наближення до розв’язку системи, для цього:

• у комірку А7 введіть текст Нульове наближення:

• у комірки А8, А9, А10 та А11 введіть текст відповідно х1=, х2=, х3= та х4=

• у комірки В8, В9, В10 та В11 введіть формули відповідно =F2/A2, =F3/A3, =F4/A4, =F5/A5.

Після цього робочий аркуш матиме вигляд:

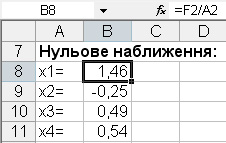
8. Знайдіть перше наближення до розв’язку системи, для цього:

• у комірку А13 введіть текст Перше наближення:

• скопіюйте у діапазон комірок А14:А17 текст з діапазону комірок А8:А11;

• у діапазон комірок В14:В17 введіть формули для обчислення першого наближення до розв’язку системи, відповідно:

=(F$2-B$2*B9-C$2*B10-D$2*B11)/A$2

=(F$3-A$3*B8-C$3*B10-D$3*B11)/B$3

=(F$4-A$4*B8-B$4*B9-D$4*B11)/C$4

=(F$5-A$5*B8-B$5*B9-C$5*B10)/D$5

9. Перевірте виконання умови

, для цього:

• у комірку D13 введіть текст Похибка:

• у комірку D14 введіть формулу =B14-B8 та скопіюйте її за допомогою автозаповнення у інші комірки діапазону D14: D17. Якщо модуль найбільшого значення у діапазоні комірок D14: D17 не менший за задану точність , переходьте до п.9, інакше отримані значення змінних і будуть шуканим розв’язком системи.

10. Знайдіть друге наближення до розв’язку системи, для цього:

• у комірку А19 введіть текст Друге наближення:

• скопіюйте у діапазон комірок А20:А23 текст з діапазону комірок А8:А11;

• у діапазон комірок В20:В23 введіть формули для обчислення другого наближення до розв’язку системи, для цього:

  • виділіть діапазон комірок В14:В17 та за допомогою буферу обміну (звичайна операція копіювання) скопіюйте формули з нього;

  • виділіть комірку В20 та вставте з буферу обміну скопійовані формули.

11. Перевірте виконання умови аналогічно до того, як це робилося у п.8. Якщо умова виконується, шуканий розв’язок отриманий, можна переходити до п.11. Якщо не виконується, продовжуйте виконувати п.9 (отримуючи наступні наближення), доки умова не буде виконана.

12. Запишіть отриманий розв’язок внизу робочого аркуша.

13. Збережіть створений файл.

14. Виконайте завдання для самостійної роботи з лабораторної роботи №1, номер завдання оберіть відповідно Вашому номеру у журналі.

15. Після виконання завдання для самостійної роботи покличте викладача для перевірки результату та захисту лабораторної роботи.