Теоретичні відомості

Задача обчислення коренів рівняння

(4.1)

часто зустрічається як при вивченні загально-технічних дисциплін, так і в інженерній практиці. Точне значення коренів рівняння (4.1) можливе лише в деяких окремих випадках. Тому широко використовуються методи знаходження наближених значень коренів рівняння вигляду (4.1) та оцінки їх точності.

Розглянемо задачу обчислення дійсних коренів рівняння (4.1), вважаючи, що функція визначена і двічі неперервно диференційовна в деякому проміжку.

Розв’язання цієї задачі складається з двох етапів:

1. Відокремлення коренів рівняння (4.1);

2. Обчислення коренів цього рівняння із заданою точністю.

Відокремлення коренів рівняння .

Під відокремленням кореня рівняння (4.1) розуміють знаходження такого проміжку [а; b] області визначення функції , в якому виконані наступні умови:

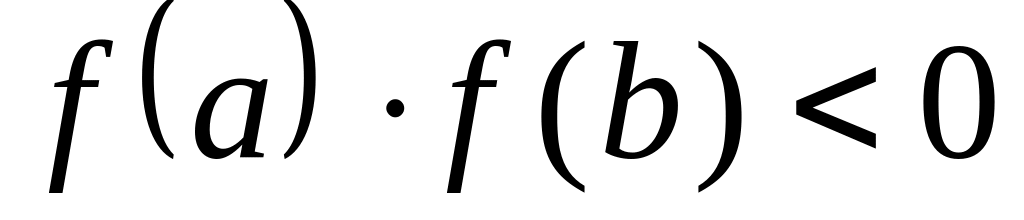1. (функція на кінцях відрізка має значення різних знаків);

2. не змінює знак на відрізку [а; b] (функція строго монотонна на відрізку [а; b]).

Виконання умови 1 гарантує існування на відрізку [а; b] хоч одного кореня рівняння (4.1), виконання умов 1, 2 забезпечує існування тільки одного кореня цього рівняння на [а; b].

Для збіжності ряду наближених методів обчислення кореня рівняння (4.1), відокремленого на відрізку [а; b], вимагається виконання на цьому відрізку ще однієї умови:

3. не змінює знак на [а; b] (крива або опукла, або вгнута на проміжку [а; b]).

В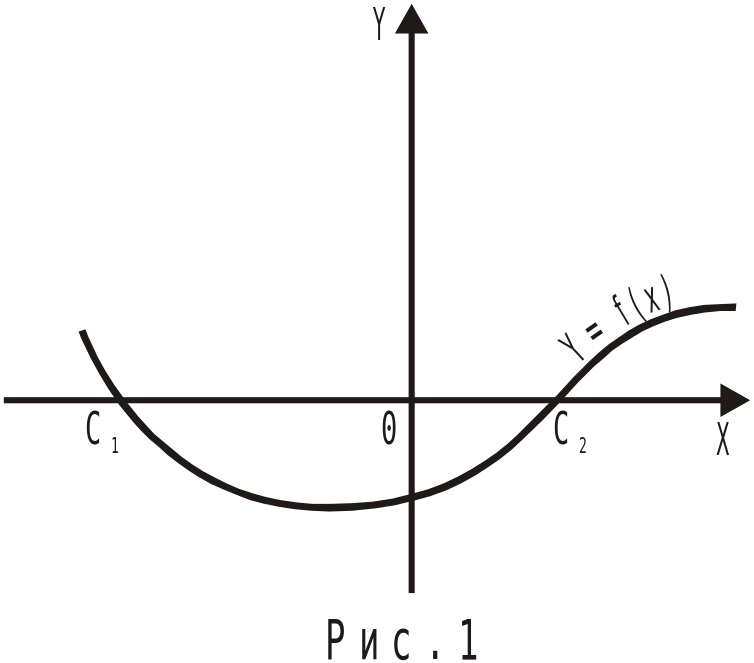 ідокремлення коренів рівняння (4.1) можна проводити як аналітично, так і графічно. Наприклад, вибираємо точку а в області визначення функції і встановлюємо знак . Далі підбираємо точку b так, щоб значення мало знак, протилежний знаку . На відрізку [а; b] встановлюємо знак похідної . Якщо не змінює знак на [а; b], то корінь рівняння (4.1) відокремлено. Інакше, відрізок [а; b] звужуємо, досягаючи виконання умов 1, 2 (а при потребі й умови 3).

Інколи простіше побудувати ескіз графіка функції , грубо встановити відрізки, що містять корені рівняння (4.1) (точки перетину кривої з віссю Ох), а потім перевірити виконання умов 1-3 (рис.1).

П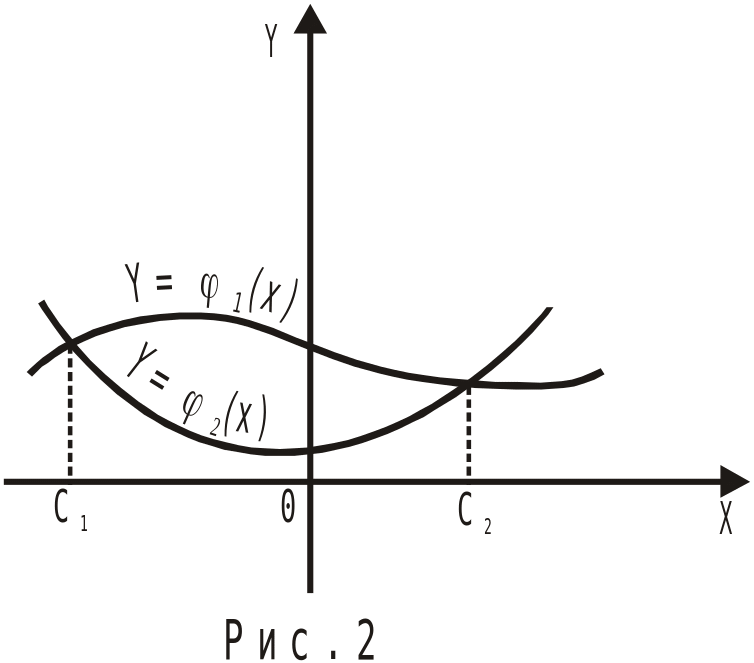 ри графічному відокремленні коренів часто доцільно рівняння (4.1) представити у вигляді і побудувати ескізи графіків функцій та . Абсциси точок перетину цих кривих дають уявлення про наближені значення коренів рівняння (4.1) (рис.2). Далі для кожного з коренів знаходять відповідний відрізок, що відокремлює цей корінь.

Обчислення коренів рівняння .

Якщо корінь рівняння (4.1) відокремлено на відрізку [а; b], наступний етап – обчислення цього кореня із заданою точністю ε, тобто знаходження такого наближеного значення ξ невідомого кореня с, щоб виконувалась нерівність .

Розглянемо кілька методів розв’язання цієї задачі.

Метод половинного поділу відрізка. Проміжок [а; b] ділимо точкою пополам і розглядаємо той з проміжків [а; с₁], [с₁; b], який містить шуканий корінь (для нього має виконуватися умова 1). Позначимо цей проміжок через [а₁; b₁]. Його довжина Для проміжку [а₁; b₁] повторюємо ту ж послідовність дій: знаходимо розглядаємо відрізки [а₁; с₂], [с₂; b₁] і беремо той з них, який містить корінь с. Позначимо його через [а₂; b₂], причому Описаний процес продовжуємо далі.

Т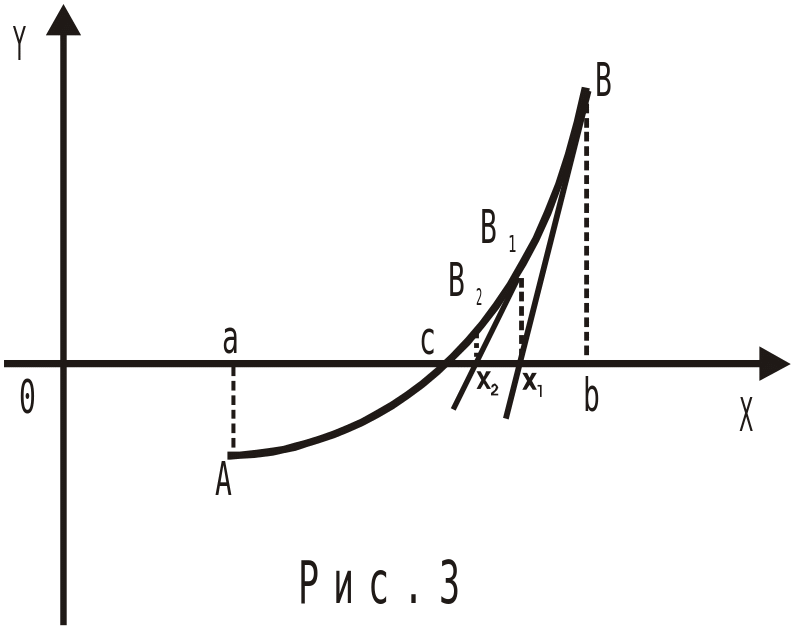 очки с₁, с₂, ..., що знаходяться в процесі обчислень, є послідовними наближеннями шуканого кореня рівняння. Процес продовжується до того часу, поки не дістанемо відрізок [а_n; b_n], що містить корінь с рівняння (4.1) і для якого виконується умова

Точка і приймається за наближене значення кореня с, знайдене з точністю ε.

При розгляді всіх наступних методів вважаємо, що корінь с рівняння (4.1) відокремлено на відрізку [а; b] (a < b), для якого виконані умови 1-3.

Метод дотичних (метод Ньютона). Нехай, для визначеності, на відрізку [а; b] і В цьому випадку , (рис.3).

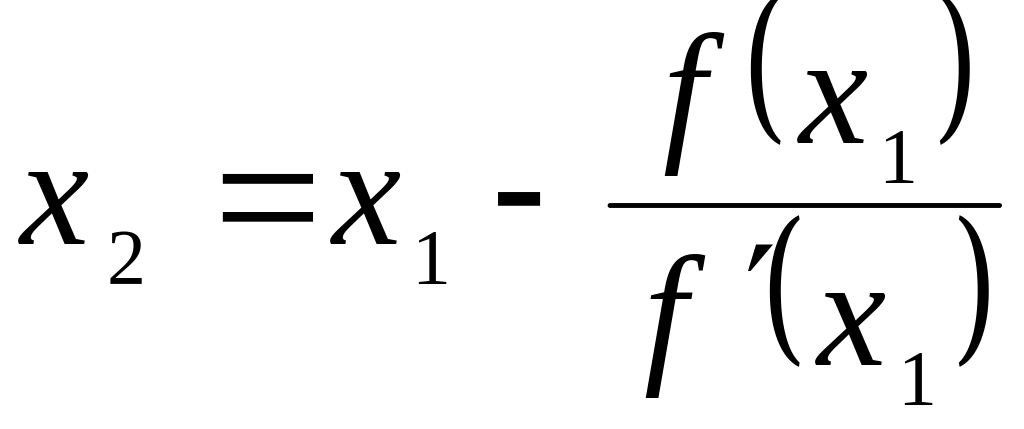Через точку B(b, f(b)) проведемо дотичну до графіка функції . Її рівняння Покладаючи , знаходимо абсцису х₁ точки перетину дотичної з віссю Ох Оскільки то х₁ < b і, враховуючи угнутість графіка функції, х₁ < с, тобто с < х₁ < b. Точку х₁ приймаємо за перше наближення кореня рівняння. Далі, виконуючи ту ж послідовність дій для відрізка [а; х₁], знаходимо друге наближення кореня (причому с < х₂ < х₁), потім третє наближення х₃ і т.д.

Розрахункова формула методу дотичних

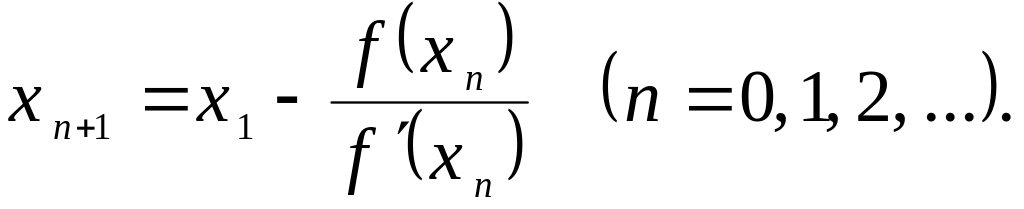(4.2)

Послідовність наближень {x_n} спадна і обмежена знизу точним значенням кореня с, тому вона має границю, яка (це легко довести) дорівнює с:

Якщо наближене значення кореня потрібно знайти з точністю ε, обчислення зупиняють при виконанні умови і покладають

Ми розглянули випадок, коли на відрізку [а; b] і Для інших можливих комбінацій знаків і слід користуватися таким правилом:

• якщо 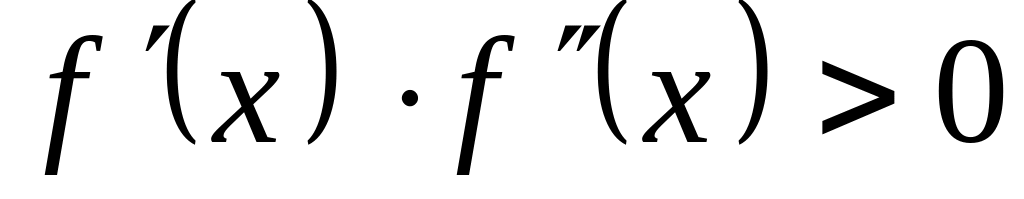на [а; b], дотичні потрібно проводити, починаючи з точки B(b, f(b)) (у формулі (4.2) х₀ = b);

• якщо ж 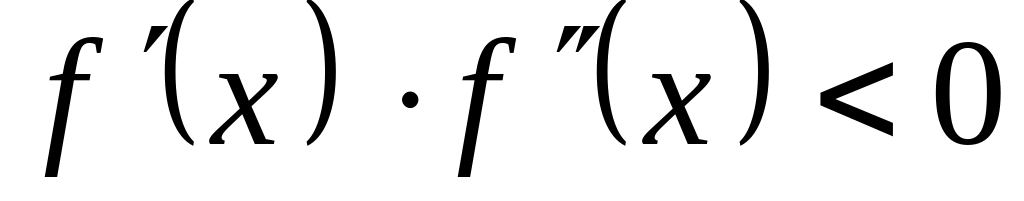на [а; b], дотичні проводять, починаючи з точки А(а, f(а)) (х₀ = а).

При цьому буде забезпечена збіжність обчислювального процесу (4.2).

Метод хорд (метод січних). Нехай знову на відрізку [а; b] і Проведемо хорду між точками А(а, f(а)) і B(b, f(b)) і знайдемо абсцису x₁ точки перетину прямої АВ з віссю Ох (рис.4).

Р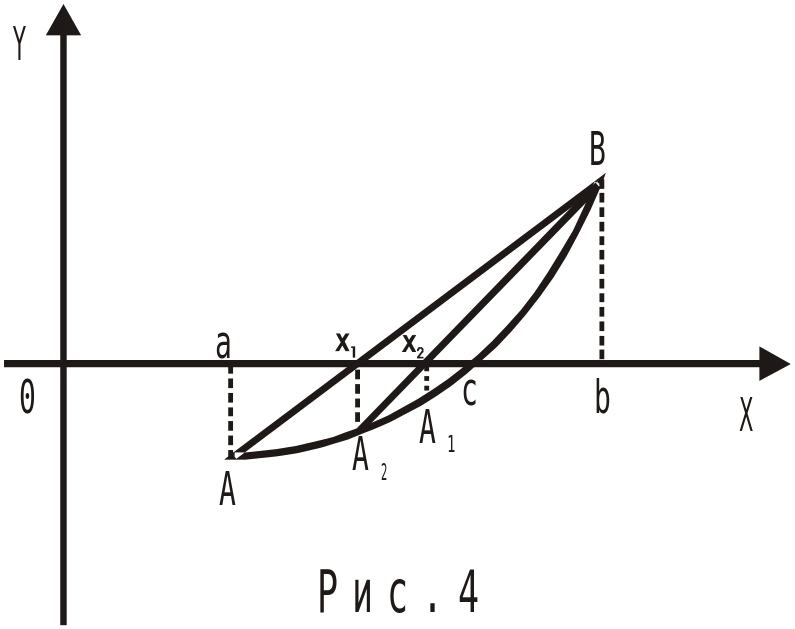 івняння прямої АВ:

При у=0 маємо причому а < х₁ < с. Далі будуємо хорду А₁В, де А₁(х₁, f(х₁)), знаходимо друге наближення кореня і т.д.

Для (n +1)-го наближення матимемо:

(4.3)

Розрахункова формула (2.3) методу хорд зберігається і для випадку, коли і на відрізку [а; b].

Якщо ж на [а; b] , то підрахунки наближень кореня с ведуться за формулою

(всі хорди в цьому випадку проходитимуть через точку А(а, f(а))).

При заданій точності ε процес обчислень зупиняють тоді, коли виконана умова .

Завдання: знайти корені рівняння .

Відокремлення коренів