
- •Міністерство аграрної політики україни
- •Міністерство аграрної політики україни
- •© Флегантов л.О., Панченко п.М., Антонець а.В., 2009 р.
- •Лабораторна робота №1.
- •Тема: Системи лінійних алгебраїчних рівнянь (метод Крамера, матричний метод)
- •Мета: Навчитись отримувати розв’язки систем лінійних алгебраїчних рівнянь методом Крамера та матричним методом
- •Теоретичні відомості
- •Лабораторна робота №2.
- •Тема: Апроксимація функцій. Мнк.
- •Мета: Навчитись знаходити параметри лінійної та квадратичної залежності за допомогою методу найменших квадратів.
- •Теоретичні відомості
- •Суть методу найменших квадратів
- •Відшукання параметрів лінійної функції
- •Відшукання параметрів квадратичної функції
- •Лабораторна робота №3.
- •Тема: Інтерполяція функцій.
- •Мета: Навчитись будувати інтерполяційний поліном та знаходити значення функції Лагранжа в довільній наперед заданій точці.
- •Теоретичні відомості
- •Теоретичні відомості
- •Запустіть програму Microsoft Excel, збережіть файл у робочу папку під назвою Розв’язування рівнянь.Xls
- •Лабораторна робота №5.
- •Тема: Наближене розв’язування систем лінійних алгебраїчних рівнянь (метод простої ітерації).
- •Теоретичні відомості
- •Теорема (достатня умова збіжності процесу ітерацій).
- •Лабораторна робота №6.
- •Тема: Наближене обчислення визначених інтегралів.
- •Мета: Навчитись обчислювати визначені інтеграли за допомогою чисельних методів.
- •Теоретичні відомості
- •Запустіть програму Microsoft Excel, збережіть файл у робочу папку під назвою Визначений інтеграл.Xls
- •Лабораторна робота №7.
- •Тема: Розв’язування звичайних диференціальних рівнянь.
- •Теоретичні відомості
- •Лабораторна робота №8.
- •Тема: Розв’язування систем звичайних диференціальних рівнянь.
- •Теоретичні відомості
- •Лабораторна робота №9.
- •Тема: Розв’язування диференціальних рівнянь у частинних похідних.
- •Мета: Навчитись знаходити розв’язки диференціальних рівнянь у частинних похідних на прикладі розрахунку величини вигину балки та розв’язання рівняння теплопровідності (Лапласа).
- •Теоретичні відомості
- •Лабораторна робота №10 Тема: Проведення кореляційного аналізу у системі statistica Мета: Навчитися процедурі проведення повного кореляційного аналізу у системі statistica.
- •Завдання
- •Побудова діаграми розсіяння
- •Розрахунок коефіцієнтів кореляції
- •Перевірка значущості коефіцієнта кореляції
- •Графічне подання результатів кореляційного аналізу
- •Завдання для самостійної роботи
- •Лабораторна робота №11 Тема: Проведення лінійного та багатофакторного регресійного аналізу у системі statistica
- •Початок роботи
- •Додаток. Основні формули
- •Література
Лабораторна робота №3.
Тема: Інтерполяція функцій.
Мета: Навчитись будувати інтерполяційний поліном та знаходити значення функції Лагранжа в довільній наперед заданій точці.
Теоретичні відомості
Широкий
клас задач в найрізноманітніших областях
природознавства пов’язаний з відновленням
по набору значень функції {yi}
у
вузлових точках {хi}
аналітичної залежності
![]() .
Звичайно функція
шукається як така, що проходить через
всі вузлові точки. Задача відшукання
такої функції називається задачею
інтерполяції,
а функцію називають інтерполяційною.
Для побудови інтерполяційної функції
вибирають набір базисних функцій та
інтерполяційну функцію шукають у вигляді
лінійної комбінації цих базисних
функцій. Інтерполяційну функцію також
часто шукають у вигляді полінома, степінь
якого на одиницю менший за кількість
вузлів.
.
Звичайно функція
шукається як така, що проходить через
всі вузлові точки. Задача відшукання
такої функції називається задачею
інтерполяції,
а функцію називають інтерполяційною.
Для побудови інтерполяційної функції
вибирають набір базисних функцій та
інтерполяційну функцію шукають у вигляді
лінійної комбінації цих базисних
функцій. Інтерполяційну функцію також
часто шукають у вигляді полінома, степінь
якого на одиницю менший за кількість
вузлів.
Можна
показати, що функція
 ,
де базисні функції
,
де базисні функції
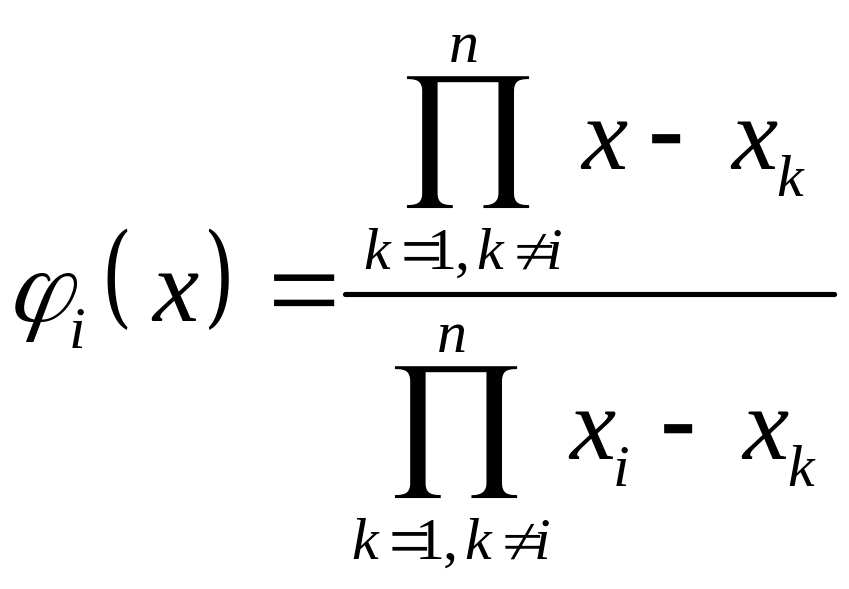 ,
є шуканим інтерполяційним поліномом-
поліномом Лагранжа. З практичної точки
зору головна проблема полягає в обчисленні
значень базисних функцій (в довільній
точці).
,
є шуканим інтерполяційним поліномом-
поліномом Лагранжа. З практичної точки
зору головна проблема полягає в обчисленні
значень базисних функцій (в довільній
точці).
Завдання:
знайти
значення базисних функцій у вузлових
точках та функії Лагранжа у точці
![]() .
.
Запустіть програму Microsoft Excel, збережіть файл у робочу папку під назвою Інтерполяція функцій.xls
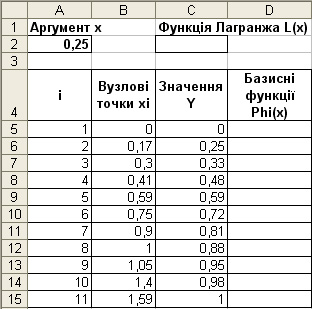
Введіть з клавіатури у комірки робочого аркуша значення Х та У з таблиці, а також значення аргумента х, для якого потрібно знайти значення функції Лагранжа. Дані розташуйте на робочому аркуші так, як показано на малюнку:
Обчисліть значення
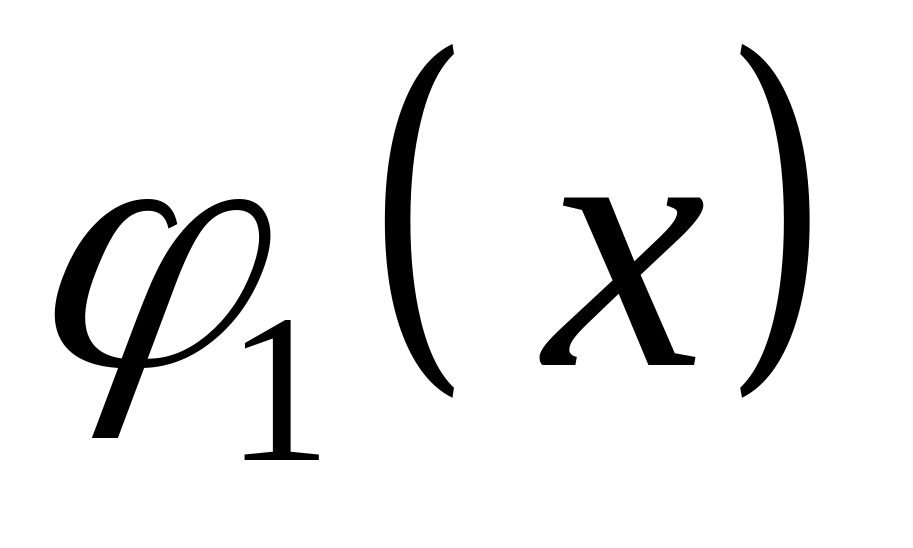 ,
для цього:
,
для цього:
Примітка.
знайдемо спочатку
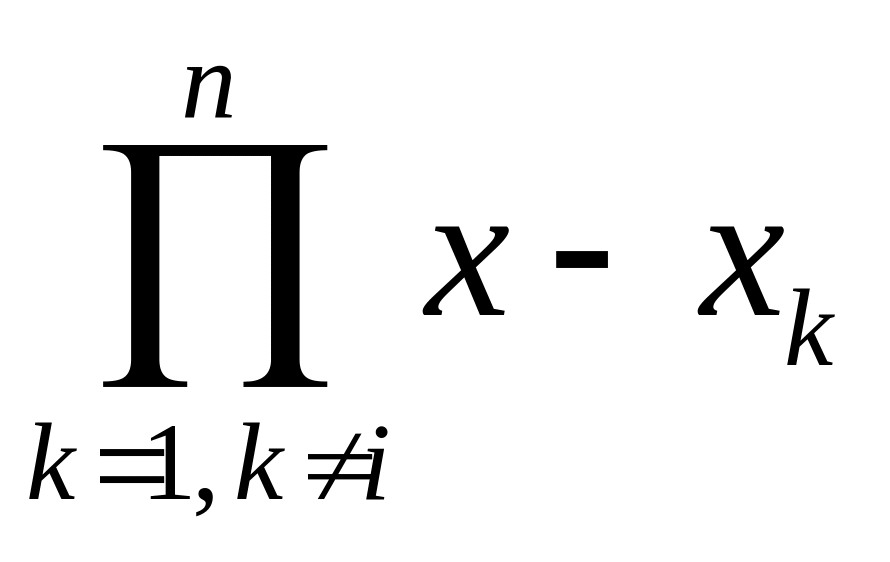 ,
де
,
де
![]() - значення, для якого потрібно обчислити
значення функції Лагранжа,
- значення, для якого потрібно обчислити
значення функції Лагранжа,
![]() - значення вузлових точок з таблиці,
тобто потрібно від
відняти кожне зі значень
з таблиці, крім значення, для якого
- значення вузлових точок з таблиці,
тобто потрібно від
відняти кожне зі значень
з таблиці, крім значення, для якого
![]() ,
а потім знайти добуток отриманих різниць.
Потім аналогічно знайдемо добуток
,
а потім знайти добуток отриманих різниць.
Потім аналогічно знайдемо добуток ,
де
,
де
![]() ,
бо
і
=
1. Після цього знайдемо частку
та
,
це і буде шукане значення
.
,
бо
і
=
1. Після цього знайдемо частку
та
,
це і буде шукане значення
.
у комірку G3 введіть формулу =А$2-B6 та скопіюйте її за допомогою автозаповнення у інші комірки діапазону G3:G12.
у комірку G13 введіть формулу =ПРОИЗВЕД(G3:G12), яка обчислюватиме добуток .
у комірку H3 введіть формулу =B$5-B6 та скопіюйте її за допомогою автозаповнення у інші комірки діапазону H3:К12.
у комірку H13 введіть формулу =ПРОИЗВЕД(H3:К12), яка обчислюватиме добуток . В результаті виконаних дій отримаєте:
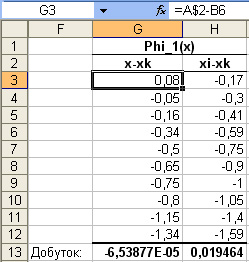
у комірку D5 введіть формулу = G13/H13, яка обчислюватиме значення .
Обчисліть значення
 ,
для цього:
,
для цього:
у комірку J3 введіть формулу =A2-B5;
у комірку K3 введіть формулу =A$2-B7 та скопіюйте її у інші комірки діапазону K3:K11;
у комірку K12 введіть формулу для обчислення добутку отриманих значень =ПРОИЗВЕД(J3:K11);
у комірку L3 введіть формулу =B6-B5;
у комірку M3 введіть формулу =B$6-B7 та скопіюйте її у інші комірки діапазону M3:M11;
у комірку M12 введіть формулу для обчислення добутку отриманих значень =ПРОИЗВЕД(L3:M11). В результаті виконаних дій отримаєте:
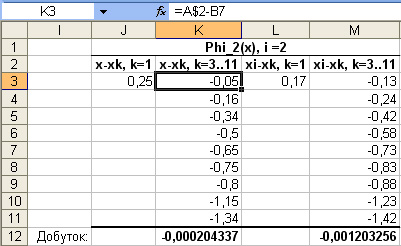
у комірку D6 введіть формулу =K12/M12, яка обчислюватиме значення .
Обчисліть значення
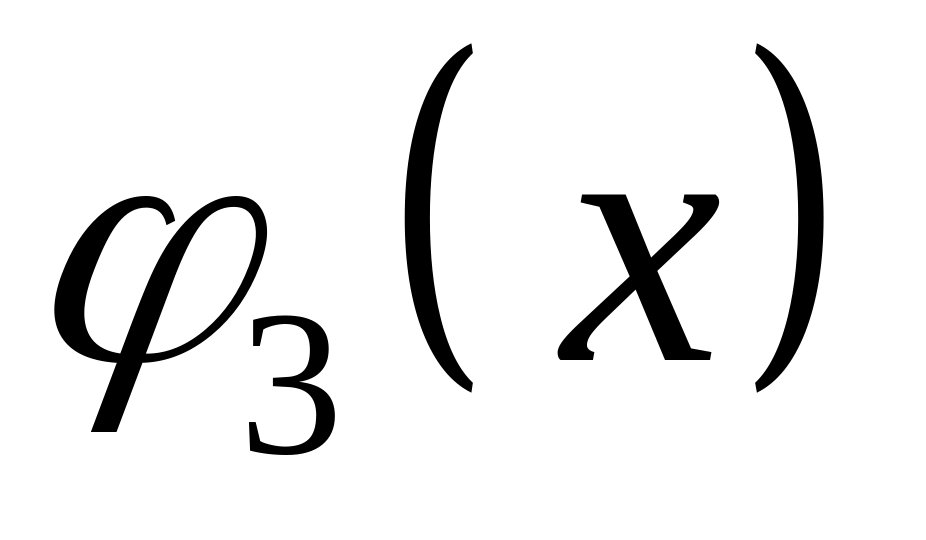 ,
для цього:
,
для цього:
у комірку P3 введіть формулу =A$2-B5 та скопіюйте її за допомогою автозаповнення у комірку P4;
у комірку Q3 введіть формулу =A$2-B8 та скопіюйте її у інші комірки діапазону Q3:Q10;
у комірку Q11 введіть формулу для обчислення добутку отриманих значень =ПРОИЗВЕД(P3:Q10);
у комірку R3 введіть формулу =B$7-B5 та скопіюйте її за допомогою автозаповнення у комірку R4;
у комірку S3 введіть формулу =B$7-B8 та скопіюйте її у інші комірки діапазону S3:S10.
у комірку S11 введіть формулу для обчислення добутку отриманих значень =ПРОИЗВЕД(R3:S10). В результаті виконаних дій отримаєте:

у комірку D7 введіть формулу =Q11/S11, яка обчислюватиме значення .
Аналогічно обчисліть всі інші значення базисних функцій
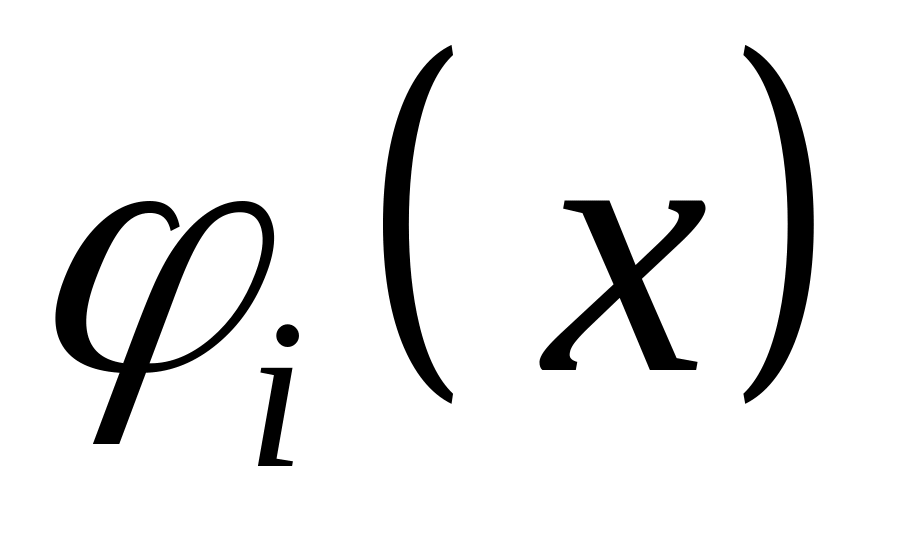 .
.Обчисліть значення функції Лагранжа як суму добутків значень функції {yi} у вузлових точках та базисних функцій .
Примітка.
Простішим
у виконанні, але складнішим для розуміння
є інший шлях отримання значень базисних
функцій
![]() ,
описаний в пп. 3-6. Замість виконання
вказаних пунктів можна було б виконати
такі дії:
,
описаний в пп. 3-6. Замість виконання
вказаних пунктів можна було б виконати
такі дії:
у комірку D5 ввести формулу
=ПРОИЗВЕД(A2-B6:B15)/ПРОИЗВЕД(B5-B6:B15)
та натиснути комбінацію клавіш Ctrl+Shift+Enter.
Перша частина формули, ПРОИЗВЕД(A2-B6:B15), обчислює добуток різниць значень в комірці A2 та в кожній з комірок діапаону B6:B15. Аналогічно друга частина формули, ПРОИЗВЕД(B5-B6:B15), обчислює добуток різниць значень в комірці B5 та в кожній з комірок діапаону B6:B15.
у комірку D6 ввести формулу
=ПРОИЗВЕД(A$2-B$5:B5;A$2-B7:B$15)/ПРОИЗВЕД(B6-B$5:B5;B6-B7:B$15)
та натиснути комбінацію клавіш Ctrl+Shift+Enter.
Перша частина формули, ПРОИЗВЕД(A$2-B$5:B5;A$2-B7:B$15), обчислює добуток різниць значень в комірці A2 та в кожній з комірок діапаону B5:B15, крім комірки B6. Аналогічно друга частина формули, ПРОИЗВЕД(B6-B$5:B5;B6-B7:B$15), обчислює добуток різниць значень в комірці B6 та в кожній з комірок діапаону B5:B15, крім комірки B6.
за допомогою автозаповнення скопіювати формулу з комірки D6 у інші комірки діапазону D6:D14.
у комірку D15 ввести формулу
=ПРОИЗВЕД(A2-B5:B14)/ПРОИЗВЕД(B15-B5:B14)
та натиснути комбінацію клавіш Ctrl+Shift+Enter.
Збережіть створений файл.
Виконайте завдання для самостійної роботи, взявши дані із завдань для самостійної роботи з лабораторної роботи №2, номер завдання оберіть відповідно Вашому номеру у журналі, значення змінної
 виберіть довільно, але так, щоб воно не
співпадало з жодним зі значень вузлових
точок та знаходилось між найменшим та
найбільшим з них.
виберіть довільно, але так, щоб воно не
співпадало з жодним зі значень вузлових
точок та знаходилось між найменшим та
найбільшим з них.Після виконання завдання для самостійної роботи покличте викладача для перевірки результату та захисту лабораторної роботи.
Лабораторна робота №4.
Тема: Наближене розв’язування алгебраїчних та трансцедентних рівнянь.
Мета: Навчитись знаходити корені алгебраїчних та трансцедентних рівнянь.
