Лабораторна робота №2.

Тема: Апроксимація функцій. Мнк.

Мета: Навчитись знаходити параметри лінійної та квадратичної залежності за допомогою методу найменших квадратів.

Теоретичні відомості

Однією з поширених задач в науці та техніці є апроксимація експериментальних даних аналітичними виразами. Для вчених це можливість підібрати параметри рівнянь таким чином, щоб його розв’язок співпадав з результатами експерименту, що часто є доказом певної теорії. Інженерам також часто необхідно описати результати вимірювань аналітично для визнячення тих чи інших фізичних параметрів.

Одним з найпоширеніших способів використання Excel для апроксимації даних є метод найменших квадратів.

Суть методу найменших квадратів

При обраному вигляді згладжувальної функції потрібно підібрати параметри та так, щоб сума квадратів відхилень від була найменшою, тобто

(2.1)

(В цьому розумінні функція за методом найменших квадратів найкращим чином описує відповідний процес).

Задача (2.1) – це задача на безумовний екстремум функції двох змінних . На підставі необхідної умови екстремуму параметри та знаходяться з умови

(2.2)

Якщо в якості згладжувальної функції вибрано (3.5), то за методом найменших квадратів параметри підбираються за критерієм

(2.3)

тобто є розв’язком слідуючої системи рівнянь:

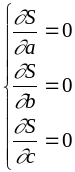(2.4)

Надалі, співвідношення (2.1) – (2.4) конкретизуються для деяких певних типів згладжувальних функцій.

Відшукання параметрів лінійної функції

Для лінійної функції

система (2.2) набуває вигляду

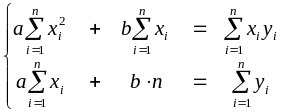(2.5)

Система (2.5) називається нормальною системою методу найменших квадратів для відшукання параметрів лінійної залежності.

Це звичайна система двох лінійних рівнянь з двома невідомими параметрами та .

Відшукання параметрів квадратичної функції

Для знаходження параметрів квадратичної функції необхідно скористатися критерієм

(2.6)

тобто, за (2.4), розв’язати систему трьох лінійних рівнянь з трьома невідомими параметрами :

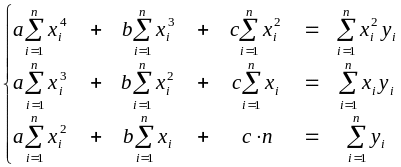
Завдання: дослідні дані зведені в таблицю значень змінних та . Побудувати точки ( ; ) в системі координат XOY. Підібрати формулу емпіричної залежності між та . Знайти за методом найменших квадратів параметри цієї залежності. Побудувати графік емпіричної залежності.

Лінійна залежність

xi	0,5	1	1,5	2	2,5	3	3,5	4
yi	-2,51	-1,03	0,48	2,11	3,36	5,01	6,71	8,02

1. Запустіть програму Microsoft Excel, збережіть файл у робочу папку під назвою МНК.xls.

2. Перейменуйте робочий аркуш Лист1 у Лінійна залежність.

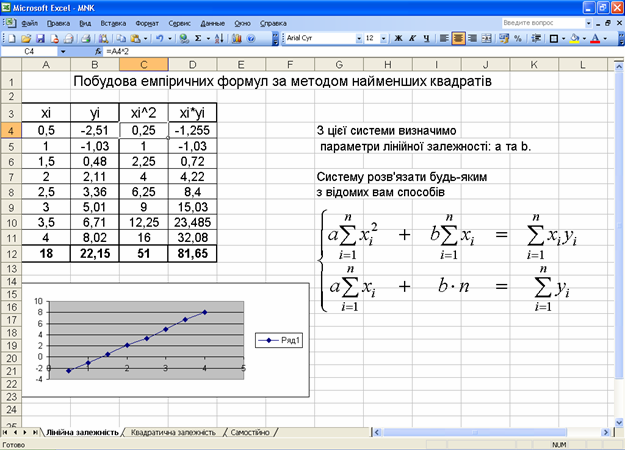
3. У діапазони А4:А11 та В4:В11 введіть відповідні значення xi, yi згідно умови.

4. Побудуйте діаграму для перших двох стовпців, переконайтесь, що дана залежність є лінійною. Побудуйте лінію тренда.

5. У комірці С4 знайдіть квадрат xi=0,5, для цього введіть формулу: =A4^2.

6. Виділіть комірку С4 і тягніть маркер автозаповнення до комірки С11.

7. В четвертому стовпці знайдіть добуток значень xi та yi, для цього в комірці D4 введіть формулу: =A4*B4.

8. Виділіть комірку D4 і тягніть маркер автозаповнення до комірки D11.

9. Знайдіть суму значень у кожному стовпці, для цього в комірці А12 введіть формулу: =СУММ(A4:A11), потім виділіть комірку А12 і тягніть маркер автозаповнення до комірки D12.

10. Підставте значення комірок А12:D12 у систему рівнянь, отримаєте систему:

11. Знайдіть параметри лінійної залежності a та b, для цього розв’яжіть систему рівнянь методом Крамера або матричним методом (лабораторна робота №1).

Квадратична залежність

xi	0,5	1	1,5	2	2,5	3	3,5	4
yi	-2,51	0,9	4	5	5,5	4,1	2,15	-1,55

12. Перейменуйте робочий аркуш Лист2 у Квадратична залежність.

13. Оформіть початок таблиці згідно малюнка.

14. В перший і другий стовпець введіть відповідні значення xi, yi згідно умови.

15. Побудуйте діаграму для перших двох стовпців. Переконайтесь, що дана залежність є квадратичною (графік має нагадувати параболу).

16. Аналогічно попередній задачі заповніть таблицю:

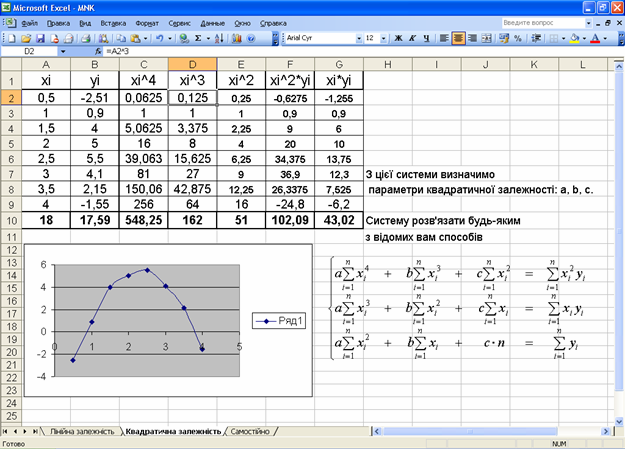
17. Підставте значення комірок діапазону А10:G10 у дану систему рівнянь з трьома невідомими: отримуємо систему:

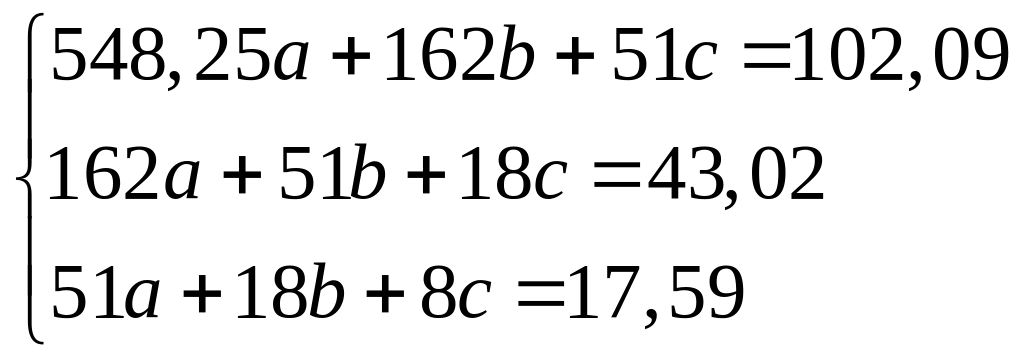
18. Знайдіть параметри лінійної залежності a, b і c, для цього розв’яжіть систему рівнянь методом Крамера або матричним методом (лабораторна робота №1).

Завдання для самостійної роботи.

Дослідні дані зведені в таблицю значень змінних та . Побудувати точки ( ; ) в системі координат OXY. Підібрати формулу емпіричної залежності між та . Знайти за методом найменших квадратів параметри цієї залежності. Оцінити середньоквадратичну похибку. Побудувати графік емпіричної залежності.

№ вар.	Значення
	0,5	1,0	1,5	2,0	2,5	3,0	3,5	4,0
	Значення
1	-2,51	-1,03	0,48	2,11	3,36	5,01	6,71	8,02
2	1,01	0,35	0,18	0,16	0,11	0,09	0,07	0,06
3	21,5	12,4	8,64	6,95	6,02	5,51	5,02	4,48
4	-0,38	1,02	1,84	2,41	2,84	3,18	3,48	3,81
5	3,25	5,45	8,91	14,7	24,4	40,1	66,1	109,1
6	5960	109,8	29,7	14,8	9,91	7,35	6,25	5,21
7	2,44	1,44	0,89	0,55	0,32	0,21	0,11	0,07
8	-0,48	3,02	13,4	31,05	61,4	97,1	170,1	254,9
9	1,26	4,01	8,24	14,2	21,3	29,9	40,3	52,1
10	3,48	5,02	7,52	11,3	15,49	21,1	27,4	35,1
11	0,01	-2,03	-3,98	-6,20	-7,95	-10,1	-12,2	-13,8
12	0,54	0,34	0,24	0,19	0,16	0,14	0,12	0,10
13	14,9	7,01	4,32	3,11	2,18	1,72	1,28	1,05
14	-1,69	-1,1	-0,58	-0,32	-0,09	-0,08	0,21	0,42
15	0,83	1,37	2,25	3,68	6,08	10,01	16,57	27,3
16	22,1	8,11	6,08	4,89	4,50	4,15	3,98	3,84
17	6,12	3,71	2,24	1,38	0,92	0,51	0,31	0,18
18	2,03	2,22	2,84	3,95	5,91	8,76	12,7	17,8
19	0,54	2,02	6,48	10,9	18,4	28,1	39,4	53,1
20	3,71	3,08	2,59	2,28	2,10	1,95	1,78	1,60
21	-7,71	-3,1	-0,43	2,02	4,43	7,12	9,53	11,9
22	0,35	0,22	0,15	0,11	0,08	0,06	0,06	0,04
23	-6,8	-2,95	-1,71	-0,95	-0,61	-0,35	-0,14	0,01
24	2,42	0,98	0,21	-0,37	-0,85	-1,23	-1,52	-1,81
25	0,3	0,74	2,03	5,48	14,9	40,1	109,8	298,5
26	10,9	6,51	5,63	5,02	4,91	4,72	4,54	4,48
27	12,3	7,45	4,51	2,73	1,88	1,09	0,62	0,34
28	-0,07	-0,75	-0,15	0,94	2,89	5,75	9,65	14,8
29	0,05	-0,01	-1,02	-3,01	-6,1	-9,93	-15,05	-21,2
30	2,71	3,02	3,23	3,39	3,63	3,71	3,89	4,05