- •Метод кодування Шеннона-Фано
- •Постановка задачи Тема: Расчет оптимального с использованием метода Шеннона-Фано. Цель работы: Освоить методику построения оптимального кода с использованием метода Шеннона-Фано.
- •Описание метода Шеннона-Фано
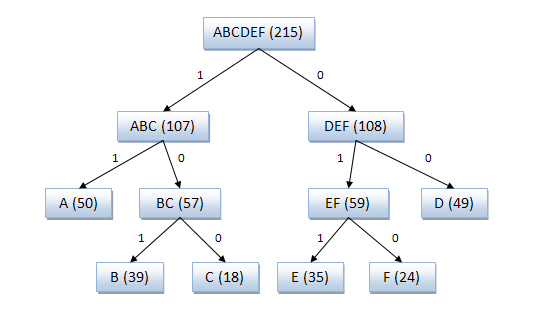
- •Кодовое дерево
- •Исходный код программ
- •Программа для нахождения среднего времени и скорости передачи
- •Программа для нахождения различный характеристик для алфавитов
- •Программа, реализующая метод Шеннона-Фано
- •Блок-схема алгоритма Шеннона-Фано
- •Блок-схема алгоритма Шеннона-Фано
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
Національний аерокосмічний університет ім. М.Є. Жуковського
“Харківський авіаційний інститут”
Кафедра комп’ютерних систем та мереж
Титульный лист заполняется на украинском языке
Остальная часть отчета может быть как на украинском, так и на русском
Розрахунково-графічна робота № 1
з дисципліни “Теорія інформації та кодування”
Метод кодування Шеннона-Фано
ХАІ.503.535.14В.050102, 1105079 ПЗ
Виконав студент гр. 535Б Сабельніков І.В.Фамилия И.О.
25.03.2014
(підпис, дата)
Перевірив канд.т.н., доцент
(науковий ступінь, вчене звання, посада)
Брежнєв Є.В.
(підпис, дата) (П.І.Б.)
Харків 2014
Постановка задачи Тема: Расчет оптимального с использованием метода Шеннона-Фано. Цель работы: Освоить методику построения оптимального кода с использованием метода Шеннона-Фано.
Для проведения расчетов разработать проект
Проeкт должен поддерживать решение следующих задач:
1.1. Число символов алфавита k = 24. Определить количество информации на символ сообщения, составленного из этого алфавита:
а) если символы алфавита встречаются с равными вероятностями;
б) если вероятности появления символов соответствуют подчиняются следующему закону

Определить, насколько недогружены символы во втором случае.
1.2. Число символов алфавита k
= 24. Длительности символов
 Вероятности появления символов алфавита
соответствуют вероятностям СВ,
распределенной по закону Пуассона (см.
выше). Величину параметра закона Пуассона
а принять равной 3,5.
Вероятности появления символов алфавита
соответствуют вероятностям СВ,
распределенной по закону Пуассона (см.
выше). Величину параметра закона Пуассона
а принять равной 3,5.
Определить скорость передачи сообщений, составленных из таких символов?
1.3. Сообщения составляются из алфавита с числом символов = k.
Вероятности появления символов алфавита соответствуют вероятностям СВ, распределенной по закону Пуассона. Величину параметра закона Пуассона а принять равной 3,5.
Найти избыточность сообщений (обусловленную неравновероятным распределением символов в сообщении), составленных из данного алфавита.
1.4 Построить оптимальный код сообщения c использованием метода Шеннона-Фано, описанного выше.
Проект должен позволять выводить на экран решение задач, указанных в 1.1 – 1.4. Для задания 1.4 необходимо обеспечить вывод кода в табличной форме с указанием вероятностей появления символа.
Описание метода Шеннона-Фано
Основные этапы:
Символы первичного алфавита m1 выписывают по убыванию вероятностей.
Символы полученного алфавита делят на две части, суммарные вероятности символов которых максимально близки друг другу.
В префиксном коде для первой части алфавита присваивается двоичная цифра «0», второй части — «1».
Полученные части рекурсивно делятся и их частям назначаются соответствующие двоичные цифры в префиксном коде.
Когда размер подалфавита становится
равен нулю или единице, то дальнейшего
удлинения префиксного кода для
соответствующих ему символов первичного
алфавита не происходит, таким образом,
алгоритм присваивает различным символам
префиксные коды разной длины. На шаге
деления алфавита существует неоднозначность,
так как разность суммарных
вероятностей ![]() может
быть одинакова для двух вариантов
разделения (учитывая, что все символы
первичного алфавита имеют вероятность
больше нуля).
может
быть одинакова для двух вариантов
разделения (учитывая, что все символы
первичного алфавита имеют вероятность
больше нуля).
Алгоритм вычисления кодов Шеннона — Фано
Код Шеннона — Фано строится с помощью дерева. Построение этого дерева начинается от корня. Всё множество кодируемых элементов соответствует корню дерева (вершине первого уровня). Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем. Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0, как в случае кода Хаффмана.
При построении кода Шеннона — Фано разбиение множества элементов может быть произведено, вообще говоря, несколькими способами. Выбор разбиения на уровне n может ухудшить варианты разбиения на следующем уровне (n + 1) и привести к неоптимальности кода в целом. Другими словами, оптимальное поведение на каждом шаге пути ещё не гарантирует оптимальности всей совокупности действий. Поэтому код Шеннона — Фано не является оптимальным в общем смысле, хотя и дает оптимальные результаты при некоторых распределениях вероятностей. Для одного и того же распределения вероятностей можно построить, вообще говоря, несколько кодов Шеннона — Фано, и все они могут дать различные результаты. Если построить все возможные коды Шеннона — Фано для данного распределения вероятностей, то среди них будут находиться и все коды Хаффмана, то есть оптимальные коды.
Пример кодового дерева
Исходные символы:
A (частота встречаемости 50)
B (частота встречаемости 39)
C (частота встречаемости 18)
D (частота встречаемости 49)
E (частота встречаемости 35)
F (частота встречаемости 24)