8.2. Методи прийняття рішень в умовах багатокритеріальності

8.2.1. Основні поняття та постановка багатокритеріальної задачі

На практиці задачі, що не мають невизначеностей, є скоріше винятком, аніж правилом. Поряд із розглянутими вище існує ще один важливий вид невизначеності — невизначеність мети, що виявляється у наявності декількох, в більшості випадків незбіжних аспектів оцінки якості того чи іншого розв'язку з множини припустимих. У формальному вигляді аспекти оцінки якості відображаються за допомогою множини критеріїв.

Таким чином виникає багатокритерійна задача дослідження операцій, загальний вигляд якої наступний:

.

Знайти розв'язок, який одночасно був би найкращим за всіма критеріями, неможливо, тому що в загальному випадку покращення значення одного з критеріїв приводить до погіршення значення іншого.

Проілюструємо геометрично задачу оптимізації за двома критеріями. При цьому вважатимемо (як і всюди надалі, окрім окремих випадків), що критерії якості максимізуються.

Розглянемо загальну задачу оптимізації за двома критеріями з двома змінними:

(2.1)

Зобразимо область припустимих розв'язків у просторі змінних (х₁,х₂) Значення критеріїв Q₁, Q₂ відображатимемо у просторі критеріїв (Q₁, Q₂). Кожній конкретній точці множини припустимих рішень відповідатиме одне і лише одне значення кожного з критеріїв , , хоча обернене твердження не завжди буде відповідати дійсності (декілька розв'язків можуть бути рівноцінними з точки зору значень критеріїв), тобто відповідне відображення буде гомоморфним. Здійснивши таку операцію для всіх точок припустимої області в просторі змінних, отримаємо її образ в просторі критеріїв:

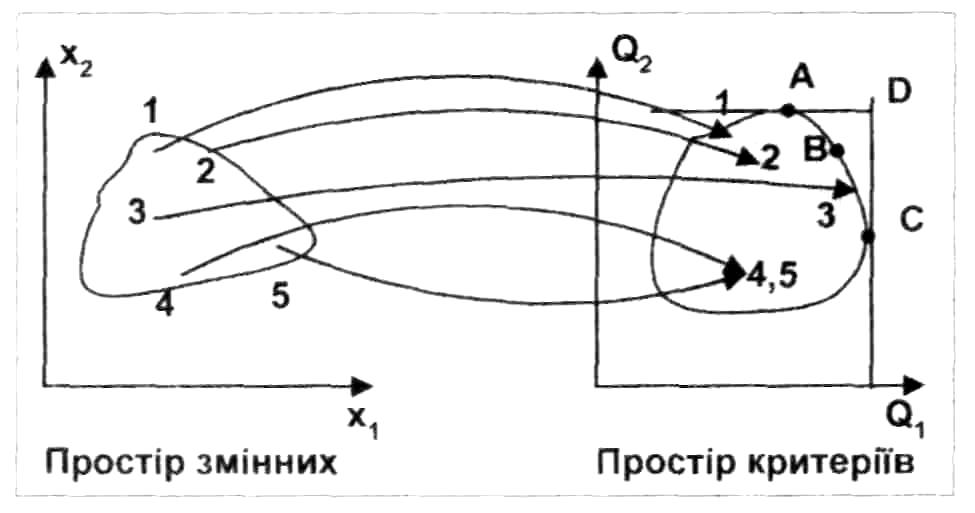
Рис. 2.1. Відображення припустимої області з простору змінних в простір критеріїв

На рис. 2.1 розв'язки 4 та 5 відображаються в одну й ту ж саму точку в просторі критеріїв, тобто є ідентичними з точки зору їх якості. Крім того, вони є гіршими, ніж розв'язки 2 та 3, у яких значення кожного з критеріїв є більші, ніж у 4 та 5. Розв'язки 1, 2, та 3 є непорівняльними, тобто без додаткової інформації неможливо визначити, який із них є кращий - значення за одним з критеріїв для них є більші, а за іншим - менші.

В той же час, аналізуючи розв'язки, що знаходяться на кривій А-В-С, можна зробити висновок, що вони є множиною "найкращих" розв'язків: для будь-якого іншого розв'язку з множини припустимих завжди знайдеться хоча б один із розв'язків, що знаходяться на А-В-С та кращий за нього (тобто такий, що його домінує). Таким чином, розв'язки, що знаходяться на А-В-С, не домінуються ніякими іншими розв'язками, що належать до припустимої області.

Множина недомінованих розв'язків багатокритерійної задачі називається множиною Парето - оптимальних розв'язків (саме Вільфредо Парето одним із перших досліджував задачі такого типу) і є, таким чином, у загальному випадку розв'язком багатокритерійної задачі. В свою чергу розв'язок належить до множини Парето - оптимальних, якщо він не домінується ніяким іншим.

8.2.2. Модель заснована на критерії сумарної ефективності

Вихідна інформація для прийняття рішень у ситуаціях цільової невизначеності, пов'язаної з наявністю декількох суперечливих цілей, представляється у вигляді базової моделі.

Використані такі позначення:

А = {А_i } - множина альтернатив;

D = {D_r} - множина критеріїв оцінки альтернатив;

К_i - підсумкова оцінка i-тої альтернативи, яка враховує її оцінки за кожним з критеріїв;

V_r - оцінка важливості r-того критерію з погляду досягнення загальної мети ;

Fir - оцінка переваги i-тої альтернативи за r-тим критерієм

Найпоширенішою нормативною моделлю прийняття рішень в умовах багатокритеріальності є модель, заснована на критерії сумарної ефективності:

(2.4)

де А_CE. - альтернатива, оптимальна за критерієм сумарної ефективності;

К_i - значення сумарної ефективності для i-тої альтернативи;

F_ir - оцінка переваги i-тої альтернативи за r-тим критерієм;

V_r - оцінка важливості r-того критерію з погляду досягнення загальної мети.

Формула (2.4) означає, що оптимальним рішенням багатокритеріальної задачі обирається та альтернатива, яка характеризується найбільшим значенням критерію сумарної ефективності.