3.3.3. Методи розв’язку скінченої гри без сідлової точки

Серед скінченних ігор, що мають практичне значення, ігри з сідловою точкою трапляються рідко. Більш типовим є випадок, коли . Такі ігри називаються іграми без сідлової точки.

Розглянемо скінченну гру , платіжна матриця якої має вид (3.31), і яка не має сідлової точки. В таких іграх, очевидно , . Якщо кожному гравцю надати можливість вибору однієї чистої стратегії, то цей вибір, зрозуміло, має визначатися принципом мінімаксу. При цьому гравець А гарантує собі виграш рівний , а гравець В - програш β. Для кожного гравця природним є питання збільшення виграшу (зменшення програшу). Пошуки такого розв'язку полягають у тому, що гравці застосовують не одну, а декілька стратегій. Вибір стратегій здійснюється випадковим чином. Тобто гравці вибирають змішані стратегії.

У грі, матриця якої має розмірність , стратегії гравця А задаються наборами ймовірностей з якими гравець застосовує свої початкові чисті стратегії. Ці набори можна розглядати як m - вимірні вектори, для компонент яких виконуються умови

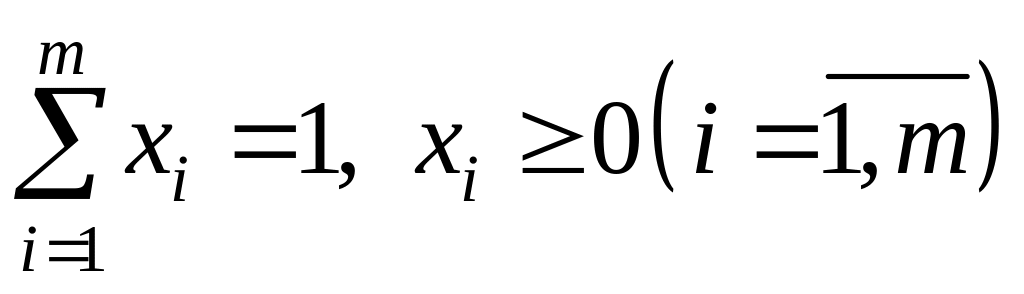(3.35)

Аналогічно стратегії гравця В задаються наборами ймовірностей які відповідають його змішаним стратегіям. Ці набори можна розглядати як n - вимірні вектори, для компонент яких виконуються умови

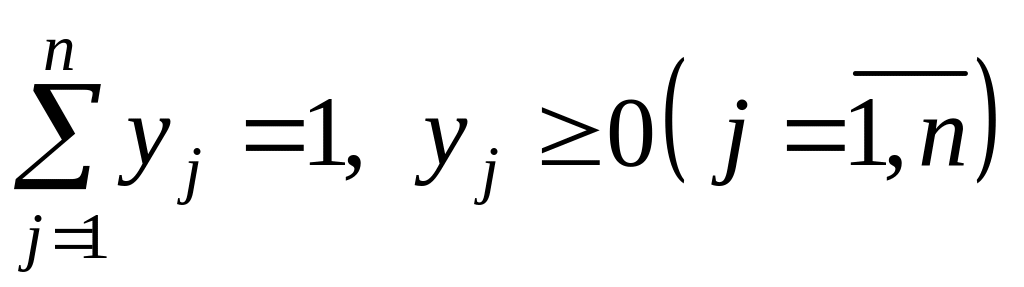(3.36)

Має місце, так звана, основна теорема теорії ігор, яка полягає в тому, що кожна скінчена гра має, принаймні, один розв'язок, можливо, в області змішаних стратегій.

Застосування оптимальної стратегії в розглядуваній задачі допомагає отримати виграш, рівний ціні гри:

Для оптимальних стратегій гравців має місце співвідношення

Спрощення ігор

Взагалі кажучи, задача розв'язування гри, якщо її матриця не містить сідлової точки, тим складніша, чим більші значення m та n. Тому в теорії матричних ігор розглядаються способи, за допомогою яких розв'язування одних ігор зводиться до розв'язування інших, більш простіших (зокрема, з допомогою скорочення розмірності матриці). Скоротити розмірність матриці можна, виключаючи дублюючі і наперед невигідні стратегії.

Дублюючими називаються стратегії, яким відповідають однакові значення елементів у платіжній матриці, тобто, якщо в платіжній матриці містяться однакові рядки чи стовпці.

Якщо ж всі елементи і-того рядка матриці менші, ніж відповідні елементи k-того рядка, то і - та стратегія для гравця А називається наперед невигідною. Або якщо елементи r - го стовпця матриці більші відповідних елементів j-того стовпця, то для гравця В стратегія наперед невигідна.

3.4. Методи експертних оцінок

Під експертними оцінками розуміють комплекс логічних і ма­тематичних процедур, спрямованих на отримання від фахівців інформації, її аналіз й узагальнення з метою підготовки і вироб­лення раціональних рішень.

Методи експертних оцінок можна поділити на дві групи: мето­ди колективної роботи експертної групи і методи отримання інди­відуальної думки членів експертної групи.

Методи колективної роботи експертної групи передбачають отримання загальної думки в ході спільного обговорення пробле­ми. Іноді ці методи називають методами прямого отримання колек­тивної думки. Основна перевага цих методів полягає в можливості різностороннього аналізу проблем.