2.3. Широкополосное согласование линий передачи

Впервые задача широкополосного согласования комплексных нагрузок из сосредоточенных элементов была поставлена и решена американским ученым Р. М. Фано в 1950 г. Фано показал, что даже при бесконечном числе степеней свободы в реактивном согласующем устройстве невозможно достичь режима чисто бегущей волны в непрерывной конечной полосе частот и что не всякую комплексную нагрузку можно согласовать в заданной полосе частот при выбранном допустимом уровне КБВ.

Выводы Фано были основаны на анализе схемы передачи мощности от согласованного генератора через синтезируемый реактивный четырехполюсник РЧП1 в комплексную нагрузку, представляемую, в свою очередь, каскадным соединением произвольного, но фиксированного реактивного четырехполюсника РЧП2 и постоянного активного сопротивления 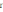(рис. 2.8,а).

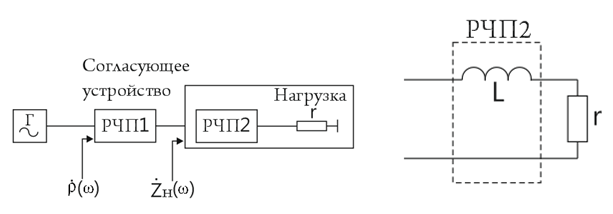
а) б)

Рис 2.8. а - схема широкополосного согласования в обобщенной форме;

б - НЧ-прототип простейшей комплексной нагрузки

Присутствие фиксированного реактивного четырехполюсника РЧП2 в эквивалентном представлении нагрузки как раз и приводит к появлению ограничений на возможности широкополосного согласования.

Как показал Фано для простейшей комплексной нагрузки в виде последовательной 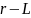- цепи (рис. 2.8,б) ограничения сводятся к неравенству

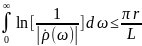(2.8)

Исходя из этого неравенства можно установить вид оптимальной частотной характеристики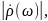 обеспечивающей максимальную полосу согласования при заданном допустимом значении 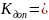. Очевидно, что в для оптимального случая величина 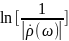должна оставаться постоянной пределах полосы согласования и равной 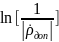, а за пределами этой полосы функция должна быть равна нулю.

Подобные оптимальные характеристики показаны на рис. 2.9 для двух значений полосы согласования. В предположении прямоугольного вида оптимальной частотной характеристики интеграл в (2.8) легко вычисляется и для оценки предельно возможной полосы согласования получаем формулу для определения граничной частоты согласования по заданному уровню минимально допустимой величины КБВ в полосе согласования

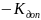
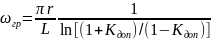(2.9)

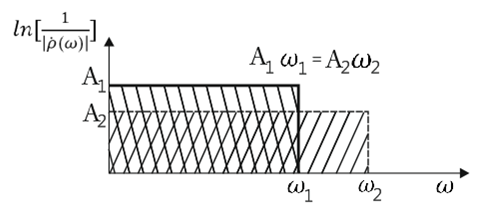
Рис. 2.9. Оптимальные частотные характеристики согласования (ω_гр1= ω_1, ω_гр2= ω₂)

Графики оптимальной и неоптимальной частотных характеристик для одного и того же значения К_доп (ρ_доп) показаны на рис 2.10.

В случае S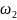₂, характеристика имеет прямоугольную форму, соответствующую постоянному уровню коэффициента отражения в полосе согласования. Во втором случае на частотах ω^'_, ω^" модуль ρ меньшее чем ρ_доп (вплоть до ρ=0). В соответствии с (2.8) в обоих случаях площадь под частотными кривыми имеет одно и то же ограничение, поэтому полоса согласования во втором случае получается меньшей (ω_1<ω₂).

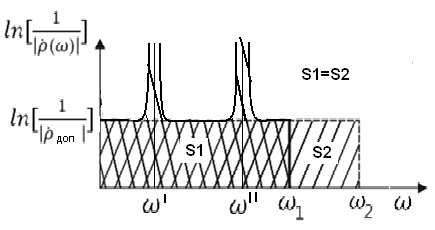
Рис. 2.10. Оптимальный (S2, ω₂) и не оптимальный (S1, ω_1, ω^'_, ω^") случаи согласования.

Приведенный пример показывает, что при расчете широкополосных согласующих цепей не следует стремиться к идеальному согласованию в одной или нескольких точках заданной полосы частот. Чем большее число точек идеального согласования комплексной нагрузки достигнуто в требуемой полосе частот, тем более глубоких провалов КБВ следует ожидать между ними.

Таким образом, для правильного решения задачи широкополосного согласования комплексной нагрузки следует стремиться к равномерному распределению допустимого рассогласования в нужной полосе частот. За пределами этой полосы рассогласование должно быть возможно большим.

Заменой частотной переменной полученный выше результат может быть перенесен на случай согласования резонансной нагрузки в виде последовательного колебательного контура с известной собственной добротностью Q₀= ω₀L/r, где ω₀ - резонансная частота. Предполагая, что частотная характеристика КБВ в окрестности резонансной частоты имеет идеальную прямоугольную форму в пределах полосы согласования 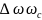находим

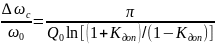(2.10)

Это соотношение показывает, что максимально возможная полоса согласования получается тем меньшей, чем выше добротность нагрузки и допустимое значение КБВ.