2. Расчёт однофазных электрических цепей переменного тока.
Переменный электрический ток – электрический ток, периодически изменяющийся с течением времени. В электрических сетях используется синусоидальный переменный ток, который возникает в цепи под действием синусоидальной ЭДС.
Синусоидальные ЭДС, ток и напряжение характеризуются следующими величинами:
амплитуда – максимальное значение синусоидальной величины (Еm, Im,
Um);
период Т – время одного полного колебания (сек);
частота f =
– число
колебаний в одну секунду (Гц);угловая частота (угловая скорость) – ω =
= 2πf;мгновенное значение – значение синусоидальной величины в любой момент времени: е = Еm sin (ωt + ψ), где ψ – начальный угол;
действующее значение тока I = 0.7*Im – значение переменного тока, эквивалентное постоянному току по тепловому действию.
Сопротивления в цепях переменного тока делятся на две группы: активные и реактивные. В активных сопротивлениях R электрическая энергия преобразуется в тепловую энергию. В реактивных сопротивлениях электрическая энергия, вырабатываемая источником, не расходуется. Реактивным сопротивлением обладают индуктивность L и ёмкость C.
Индуктивность L – элемент электрической цепи, способный запасать энергию магнитного поля. Катушка с индуктивностью L, у которой R = 0 и C = 0, называется идеальной.
Ёмкость C – элемент электрической цепи, способный запасать энергию электрического поля. Конденсатор с ёмкостью C, у которого R = 0 и L = 0, называется идеальным.
В реальных катушке L и конденсаторе C активное сопротивление R ≠ 0.
Для расчёта цепей переменного тока применяют уравнения и векторные диаграммы.
Для наглядности синусоидальные величины изображают векторами, вращающимися против часовой стрелки со скоростью, равной угловой частоте ω этих синусоид. Так как эти векторы изображают синусоиды в начальный момент времени, то они неподвижны. Длина вектора в выбранном масштабе определяется амплитудой синусоиды, а угол поворота равен начальной фазе синусоиды. Таким образом, вектор учитывает все значения, характеризующие синусоидальную величину: амплитуду, угловую частоту и начальную фазу.
При построении векторов положительные углы отсчитывают от положительного направления горизонтальной оси против вращения часовой стрелки, а отрицательные – по её движению.
Сложение и вычитание векторов осуществляется по правилу многоугольника, известного из математики.
Совокупность векторов, изображающих на одном чертеже несколько синусоидальных величин одинаковой частоты в начальный момент времени, называется векторной диаграммой.
Мощность
однофазного тока: полная мощность
·
BA,
где
·
,
·
·
cosφ
– активная мощность, Вт
=
·
·sinφ
- реактивная
мощность:
·
·
- индуктивная
мощность, Вар;
·
·
- ёмкостная
мощность, Вар
В цепи с последовательным соединением активного сопротивления R и ёмкости C протекает синусоидальный ток i = Im*sinωt, который создаёт падение напряжения на активном сопротивлении Ua и на ёмкостном сопротивлении Uc.
Напряжение на активном сопротивлении Ua совпадает по фазе с током, а напряжение на ёмкости Uc отстаёт по фазе от тока на угол φ = 90°.
Общее
напряжение цепи равно:
(вектора напряжений)
Ток
в цепи равен:
,
где
;
Ёмкостное
сопротивление:
Коэффициент
мощности цепи:
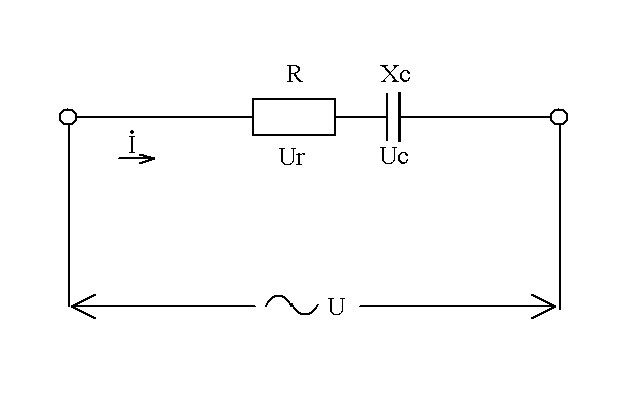Пример
Дано:
напряжение
,
ёмкость
конденсатора
,
активное
сопротивление
.
Найти:
ёмкостное сопротивление
,
ток
,
активное
напряжение
,
полное напряжение .
Построить векторную диаграмму.
Решение
Находим ёмкостное сопротивление:
Находим ток в цепи:
3. Находим активное напряжение:
4. Находим полное напряжение:
5. Строим векторную диаграмму , выбрав масштаб напряжений
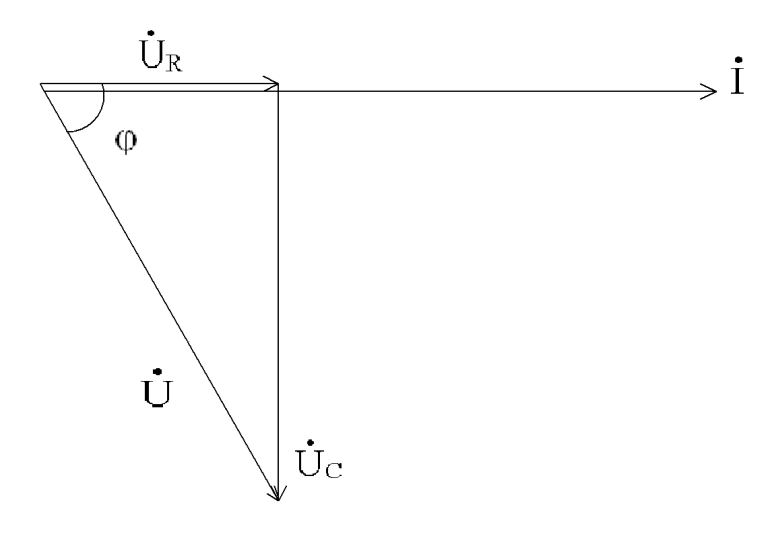
В цепи с последовательным соединением активного сопротивления R и индуктивности L протекает синусоидальный ток i = Im sinωt, который создаёт падение напряжения на активном сопротивлении Ua и на индуктивном сопротивлении UL.
Напряжение на активном сопротивлении Ua совпадает по фазе с током, а напряжение на индуктивности UL опережает по фазе ток на угол φ = 90°.
Общее
напряжение цепи равно:
(вектора напряжений)
Ток
в цепи равен:
,
где
;
Индуктивное
сопротивление:
=2
·
Коэффициент мощности цепи:
Пример
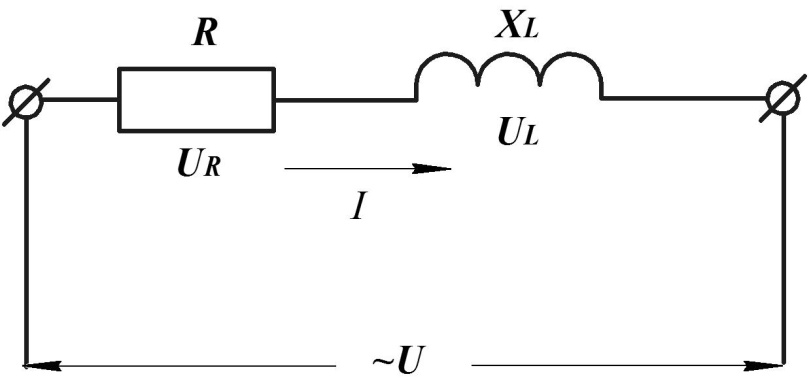
Дано:
напряжение U = 200 В; ток I = 10 А; частота f = 100 Гц;
активная мощность P = 1600 ВТ.
Найти: сопротивления R и XL . Построить векторную диаграмму напряжений.
Решение
Находим активное сопротивление:
;
Ом
Находим полное сопротивление цепи:
Ом
Находим индуктивное сопротивление:
Ом;
Находим напряжения на участках цепи:
;
В
Строим векторную диаграмму, выбрав масштаб ΜU=20 В/см
