1. Тягово-скоростные свойства атс. Оценочные показатели. Методика определения.

Тягово-скоростными называют свойства АТС, определяющие воз­можные по ха­рактеристикам двигателя или сцепления ведущих колес с до­рогой диапазоны измене­ния скоростей движения и предельные интенсив­ности разгона на тяговом режиме в различ­ных дорожных и нагрузочных условиях. Тяговым принято считать режим, при котором от двигателя к ведущим колесам подводится мощность, достаточная для пре­одоления со­противлений движению.

Для сравнительной оценки тягово-скоростных свойств наиболее употребитель­ными и достаточными являются следующие показатели:

- максимальная скорость;

- условная максимальная скорость;

- время разгона на пути 400 и 1000 м;

- время разгона до заданной скорости;

- скоростная характеристика – «разгон-выбег»;

- скоростная характеристика разгона на высшей передаче;

- топливно-скоростная характеристика на дороге с переменным про­дольным про­филем;

- минимальная устойчивая скорость на высшей передаче;

- максимальный преодолеваемый подъем;

- установившаяся скорость на затяжных подъемах;

- ускорения при разгоне;

- сила тяги на крюке;

- длина динамически преодолеваемого подъема.

Приведенные выше оценочные параметры (характеристики) могут быть полу­чены как экспериментально, так и расчетным способом. Методы определения оценочных показателей. Эксперименталь­ный, графический, расчетнвй.

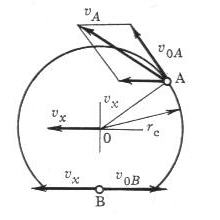
2. Кинематика и динамика автомобильного колеса. Режимы качения колеса; схема действующих сил.

Пневматическая шина представляет собой оболочку, напол­ненную сжатым воздухом. При каче­нии колеса по дороге происходит де­формация этой оболочки и проскальзывание элементов протектора относи­тельно поверхности дороги.

Размер автомобильного колеса в свободном, ненагруженном состоянии характеризуется свободным радиусом r_c. Свободный радиус колеса — поло­вина наружного диаметра D_н;

r_c =0.5 D_н.

Под наружным диаметром колеса понимается   диаметр   наибольшего окружного сечения беговой дорожки колеса при отсутствии контакта с доро­гой. Наружный диаметр колеса зави­сит от давления воздуха в шине и, как правило, возрастает с его увеличением, определяется непосредственно замером. Значение наружного диаметра колеса при номинальном давлении воздуха в шине указывается в ГОСТах или ка­талогах.  Статический радиус при известных конструктивных параметрах шин можно находить из соотношения:

r_ст =0,5d+l_zH,

где d — посадочный диаметр обода ши­ны;

l_z —коэффициент вертикальной деформации, зависящий от типа шин:

для тороидных шин l_z =0,85...0,87;

для шин с регулируемым давлением и ароч­ных l_z =0,8...0,85;

Н — высота профиля.

При качении нагруженного колеса в силу ряда причин (динамическое действие нагрузки, передаваемый колесом крутящий момент, скорость вра­щения и др.) расстояние между осью колеса и опорной поверхностью меня­ется. Это расстояние называют дина­мическим радиусом r_д. При качении ко­леса по твердой опорной поверхности с малой скоростью статический и ди­намический радиусы его практически одинаковы. Поэтому при приближен­ных расчетах динамический радиус ча­сто принимают равным статическому.

Радиус качения колеса можно пред­ставить как радиус условного недеформируемого кольца, которое, катясь без скольжения, совершит число оборотов и пройдет путь, одинаковый с реаль­ным колесом. Радиус качения колеса является условной величиной и непосредственно не связан с его размерами. ОНопределяется как отношение поступательной скорости колеса к угловой скорости его вращения  r_k = v_x /w_k. Если направление передаваемого момента будет противоположным направлению угловой скорости вращения колеса (тормозящее колесо), при увеличении момента радиус качения будет возра­стать.

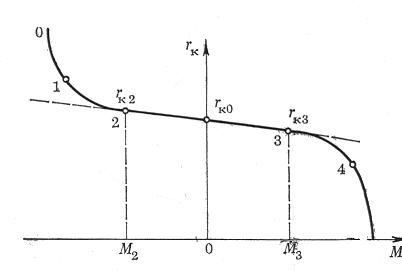Зависимость радиуса качения ко­леса от передаваемого ему крутящего момента показана на рис. 1.6. На уча­стке 2—3 радиус качения линейно за­висит от передаваемого момента, и его изменение определяется упругим проскальзыванием колеса. Акад. Е. А. Чудаковым, впервые установившим эту зависимость, предложена следующая формула для нахождения радиуса качения по передаваемому колесу мо­менту:

r_k=r_k0-l_tM_k               (1.2)

где r_k0 — радиус качения при нулевом крутящем моменте, который соответ­ствует радиусу качения колеса в ведо­мом режиме;

l_t — коэффициент тан­генциальной эластичности шины, зави­сящий от типа и конструкции шины.

На участках 1—2 и 3—4 изменение радиуса качения определяется как упругим проскальзыванием, так и скольжением колеса. Пунктирной ли­нией на графике показано, как изме­нялся бы радиус качения при отсутст­вии скольжения. Очевидно, что на участках 1—2 и 3—4 он может нахо­диться также по формуле (1.2). В по­следующем радиус качения, опреде­ленный при отсутствии скольжения, будем называть радиусом качения без скольжения и обозначать r₀.

На участках 0—1 и 4—5 происхо­дит полное скольжение элементов ши­ны относительно опорной поверхности. Точка 5 соответствует буксующему ко­лесу при неподвижном автомобиле, а точка 0—колесу, движущемуся юзом.