II. Демонстрационный пример выполнения задания

Имеются данные о величинах объема реализации продукции у- некоторой фирмы (i – порядковый номер вида продукции), которые зависят от цены каждого вида продукции и расходов на рекламу (табл. 2.1).

Таблица 2.1

Зависимость объема реализации уi, руб. От цены продукции хi1, руб. И расходов на рекламу хi2, руб.

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
yi	23	18	27	29	43	23	55	47	35	38	14	51	20	39	35
xi1	37	33	15	36	26	24	15	33	44	34	63	8	44	43	31
xi2	39	40	35	48	53	42	54	54	50	53	46	50	43	55	51

Задание

1. Построить выборочное уравнение линейной множественной регрессии (найти вектор коэффициентов b).

2. Рассчитать общую сумму квадратов Q, сумму квадратов, объясненную регрессией Q_r, остаточную сумму квадратов Q_e, несмещенные оценки соответствующих дисперсий , , и средних квадратических отклонений s, s_r, s_e. Найти стандартные отклонения коэффициентов регрессии . С доверительной вероятностью γ = 0,95 оценить значимость коэффициентов регрессии и для значимых коэффициентов определить доверительные интервалы.

3. Рассчитать выборочный множественный коэффициент детерминации , используя общую формулу и выражение через определители соответствующих матриц выборочных парных коэффициентов корреляции, и найти значение скорректированного коэффициента .

4. С доверительной вероятностью γ = 0,95 оценить значимость уравнения регрессии и найти доверительные интервалы для отдельных значений y_i.

5. Проверить полученные результаты с помощью стандартных статистических функций ТЕНДЕНЦИЯ, ЛИНЕЙН и программы РЕГРЕССИЯ из пакета анализа Microsoft Excel.

Решение

1. Для определения параметров выборочного уравнения линейной регрессии строим расчетную таблицу (табл.2.2, столбцы 1-4).

Таблица 2.2

Расчетная таблица

i	yi	xi1	xi2
1	2	3	4	5	6	7	8	9	10	11	12
1	23	37	39	17,8	102,7	234,7	26/9	17,4	4,2	8.7	26,9
2	18	33	40	21,5	229,0	135,8	12,1	16,9	4,1	12,5	30,4
3	27	15	35	23,7	37,6	88,8 '	10,8	20,9	4,6	13,7	33,7
4	29	36	48	31,9	17,1	1,6	8,3	15,5	3,9	23,3	40,5
5	43	26	53	44,8	97,4	136,5	3,3	16,4	4,0	36,0	53,6
6	23	24	42	29,4	102,7	14,2	40,5	16,5	4,1	20,5	38,2
7	55	15	54	52,3	478,2	366,4	7,4	18,2	4,3	43,0	61,6
8	47	33	54	42,5	192,3	88,3	20,0	16,5	4,1	33,7	51,4
9	35	44	50	30,6	3,5	6,6	19,7	16,3	4,0	21,8	39,3
10	38	34	53	40,5	23,7	54,1	6,2	16,2	4,0	31,7	49,2
11	14	63	46	14,3	366,1	356,1	0.1	20,5	4,5	4,4	24.1
12	51	8	50	50,1	319,2	286,2	0,9	18,8	4,3	40,6	59,5
13	20	44	43	20,0	172,5	171,5	0,0	16,7	4,1	31,1	28,9
14	39	43	55	38,6	34,4	30,1	0,1	17,4	4,2	29,5	47,7
15	35	31	51	39,1	3,5	35,6	16,8	15,7	4,0	30,5	47,7
Z					2179,7	2006,6	173,2
ср.	33,1
					155,7	1003,3	14,4
					12.5	31,7	3,8

2. Определяем выборочные коэффициенты уравнения регрессии.

Строим матрицу X объясняющих переменных размером 15×3, в которой первый столбец с единичными элементами соответствует умножению коэффициента b₀ на единицу:

.

Построим транспонированную матрицу X^Т:

• копируем матрицу X в буфер обмена и выделяем все ячейки, в которых будет содержаться матрица X^Т;

• вызываем Мастер функций, в категории Ссылки и массивы используем стандартную функцию ТРАНСП (X) и контролируем результат в ее окне (первый элемент массива X^Т) х₁₁ = 1;

• для получения массива результатов нажимаем комбинацию клавиш Ctrl+Shift+Enter.

Транспонированная матрица имеет вид:

.

Определяем произведения матриц Х^TХ с помощью стандартной функций МУМНОЖ (Х^T; X) из категории Математические, предварительно выделив для вывода результата массив размером 3×3:

Убеждаемся, что полученная матрица является симметричной.

Аналогичным образом находим произведение X^Tу, имея в виду, что результат представляет собой вектор из трех элементов:

.

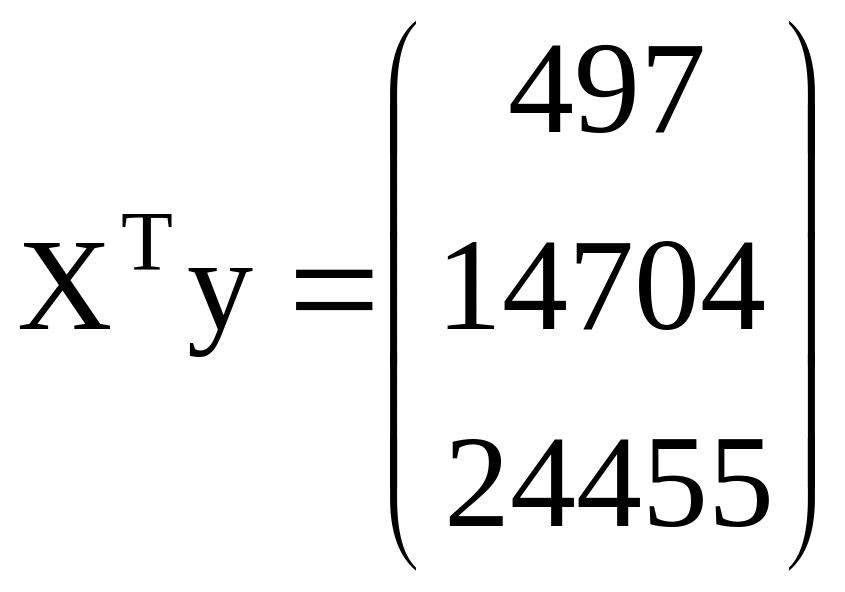Рассчитываем обратную матрицу (Х^TХ)^-1, предварительно выделяя для вывода результата массив размером 3×3 и используя стандартную математическую функцию МОБР (Х^TХ):

.

Видим, что результат представляет собой симметричную матрицу 3-го порядка.

С помощью математической функции МУМНОЖ ((Х^TХ)^-1; Х^Tу) по формуле определяем вектор выборочных оценок коэффициентов, предварительно выделив для вывода результата столбец из трех ячеек:

.

Величина коэффициента b₁ показывает, что с увеличением цены продукции на 1 руб. при фиксированных расходах на рекламу объем реализации продукции уменьшается в среднем на 0,54 руб.

С другой стороны, из полученного значения коэффициента b₂ следует, что с увеличением расходов на рекламу на 1 руб. при неизменной цене продукции, объем реализации в среднем возрастает на 1,5 руб.

Параметр b₀ мы не интерпретируем, поскольку в выборке отсутствуют значения факторных признаков, близкие к нулю.

3. Подставляя рассчитанные значения b₀, b₁ и b₂ в выборочное уравнение регрессии , находим значения (i = 1, 2, ..., n) и сводим их в 5-й столбец табл. 2.2.

Вычисляем значения , , (табл. 2.2, столбцы 6-8) и по формулам из табл. 2.1, 2.2 рассчитываем соответствующие суммы квадратов, дисперсии на степень свободы и средние кхуй суй хуйловадратические отклонения:

; ; s=12,48;

; ; ;

; .

Предварительно сформировав вспомогательный вектор из диагональных элементов [(X^TХ)^-1]_jj матрицы (X^TХ)^-1 по формулам (1.14), (1.15) находим векторы несмещенных оценок дисперсий и стандартных отклонений коэффициентов регрессии:

;

.

Теперь выборочное уравнение регрессии можно записать в общепринятом виде, указывая в скобках под коэффициентами их стандартные отклонения:

.

Из уравнения видно, что стандартные отклонения существенно меньше полученных значений оценок коэффициентов регрессии. Это позволяет предположить, что все коэффициенты регрессии значимы.

Согласно (1.20,) формируем вектор t-статистик критерия значимости коэффициентов регрессии:

.

Для заданной доверительной вероятности γ = 0,95 (уровня значимости α = 0,05) находим значение t_кр с помощью стандартной статистической функции СТЬЮДРАСПОБР(α; n – р – 1):

t_кр = t_кр(α; k = n – р – 1) = 2,179 (n – p – 1 = 15 – 2 – 1 = 12)

Поскольку , с доверительным уровнем значимости 95% делаем вывод о том, что коэффициенты β₀ , β₁ и β₂ значимы.

Вычисляем вектор P-значений для коэффициентов с помощью стандартной функции СТЬЮДРАСП ( ; n – p – 1; 2):

В силу того, что , вывод о значимости коэффициентов регрессии подтверждается.

В соответствии с (1.21) векторы нижних и верхних границ доверительного интервала коэффициентов регрессии β_j (значения нижних и верхних g·100%) найдем по формулам

;

4. Рассчитываем значения выборочных множественных коэффициентов детерминации и корреляции по формуле (1.25):

, .

Величина коэффициента показывает, что 92% вариации зависимой переменной обусловлены влиянием включенных факторов, а остальные 8% – влиянием других неучтенных в модели и случайных факторов.

Для использования эквивалентного выражения (1.26), определяющего коэффициент , сформируем матрицу парной корреляции R^ двумя способами.

Сначала последовательно находим элементы матрицы R_yX с помощью статистической функции КОРРЕЛ (·;) с аргументами у, x_j и х_k соответственно при j, k = 1, 2:

.

Затем проверяем полученные значения, используя инструмент КОРРЕЛЯЦИЯ из пакета анализа. Для этого выполняем следующие операции:

• в окне Анализ данных выбираем инструмент Корреляция;

• в категории Входные данные в поле Входной интервал вводим значения векторов у, х₁ и х₂, ставим переключатель Группирование в положение По столбцам, а поле Метки оставляем пустым;

• в категории Параметры вывода ставим переключатель в положение Выходной интервал и вводим ссылку для левой верхней ячейки интервала, в который выводятся результаты на текущем рабочем листе.

В результате получаем корреляционную матрицу (табл. 2.3).

Таблица 2.3

Корреляционная матрица

	Столбец 1	Столбец 2	Столбец 3
Столбец 1	1
Столбец 2	– 0,579870271	1
Столбец 3	0,749596657	0,025106765	1

Из найденной матрицы R_yX формируем матрицу межфакторной парной корреляции

и, используя математическую функцию МОПРЕД (·) с соответствующими массивами R_yX и R_XX в качестве аргументов, получаем

.

Скорректированный коэффициент детерминации согласно (1.32) определяем по следующим формулам:

5. Рассчитываем значение F-статистики:

.

Критическое значение для доверительного уровня γ = 0,95 (уровня значимости α = 0,05) находим с помощью стандартной статистической функции FPACIIOBP (α; р; n – р – 1):

F_кp = F_кp(α; k_l = p, k₂ = n – р – 1) = 3,89.

В силу того, что F > F_кp, с доверительным уровнем 0,95 делаем вывод о том, что уравнение регрессии значимо.

Вычисляем величину P-значения с помощью стандартной статистической функции FPACII (F; p; n – р – 1):

Р = 2,51·10^-7.

Поскольку Р < α, вывод о значимости уравнения регрессии подтверждается.

Для получения доверительного интервала для отдельных значений зависимой переменной у_i находим несмещенную оценку дисперсии регрессионного прогноза по формуле (1.43), проводя расчеты скалярных величин с помощью комбинации стандартных функций МУМНОЖ (МУМНОЖ ( ). При этом в качестве вектора-строки берем i-ю строку матрицы X, а в качестве вектора х_i – i-й столбец матрицы X^T. Полученные значения , сводим в столбцы 9, 10 табл. 2.2.

Нижние у_imin и верхние y_imax границы доверительного интервала для индивидуальных значений y_i определяем по формулам:

; ; t_кp = t_кp(α; k = n – р – 1)

и сводим их величины в табл. 2.2, столбцы 11, 12.

6. Для определения значений результативного признака по линейному уравнению регрессии с помощью стандартной статистической функции ТЕНДЕНЦИЯ выполняем следующие операции:

• в расчетной табл. 2.2. озаглавливаем 13-й столбец (например, символом y_p или словом «тенденция») и выделяем 15 значащих позиций этого столбца (i = 1, 2, ..., n);

• с помощью Мастера функций выбираем статистическую функцию ТЕНДЕНЦИЯ;

• в поля Изв_знач_у и Изв_знач_х вводим значения массива у и массивов x₁, x₂ соответственно,

• поле Нов_ знач_х оставляем пустым (при этом предполагается, что Нов_знач_х совпадают с Изв_знач_х);

• поле Константа оставляем пустым (если Константа имеет значение ИСТИНА, 1 или опущена, то коэффициент b₀ вычисляется обычным образом, если Константа имеет значение ЛОЖЬ или 0, то коэффициент b₀ полагается равным нулю);

• контролируем результат решения в окне функции (первый элемент массива) ;

• для получения массива результатов (вывода формулы массива) нажимаем комбинацию клавиш Ctrl+Shift+Enter (в выделенном столбце появятся результаты вычислений).

Для определения параметров линейного уравнения регрессии с помощью стандартной статистической функции ЛИНЕЙН выполняем следующие операции:

• с целью лучшего восприятия результатов строим вспомогательную таблицу, которая в наших обозначениях имеет вид (табл.2.4), и выделяем в ней свободные ячейки;

Таблица 2.4