9. Скорректированный коэффициент детерминации

Скорректированный (adjusted) коэффициент детерминации содержит поправки на число степеней свободы и определяется выражением

(1.34)

Коэффициент также называют адаптированным, нормированным и, иногда не совсем правильно, исправленным выборочным коэффициентом детерминации.

Свойства коэффициента :

1.

2. Коэффициент при выполнении 5-го условия КЛММР является состоятельной и, в отличие от , несмещенной оценкой генерального коэффициента детерминации ( ).

3. , но может принимать отрицательные значения.

4. В отличие от , величина может уменьшиться при добавлении в модель новых регрессоров, не оказывающих существенного влияния на зависимую переменную.

10. Оценка значимости уравнения регрессии

Для оценки значимости уравнения регрессии естественно использовать величину

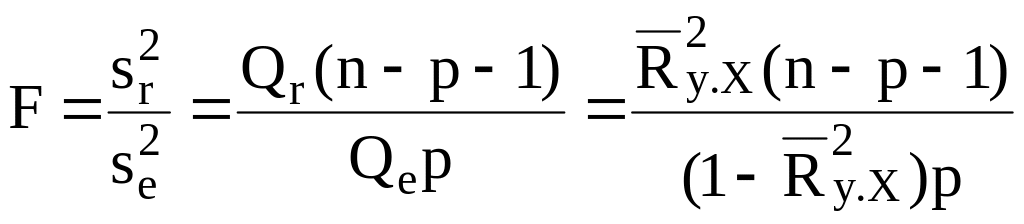, (1.35)

показывающую, во сколько раз дисперсия, объясненная регрессией, превышает остаточную. При отсутствии какой бы то ни было линейной статистической связи между зависимой и совокупностью объясняющих переменных (при β_j = 0, j = 1, 2, ..., р) факторная и остаточная дисперсии будут близкими друг к другу и величина F будет мала. При этом статистика (1.33) будет иметь распределение Фишера – Снедекора (F-распределение) с k₁ = р и k₂ = n – р – 1 степенями свободы (рис. 1.2).

Следовательно, нулевая гипотеза о не значимости уравнения регрессии в целом (об одновременном равенстве нулю всех коэффициентов при факторных переменных) составляет Н₀: β₁ = β₂ = … = β_р.

Рис. 1.2. Плотность распределения вероятностей Фишера – Снедекора

с k₁ = 5, k₂ = 20 степенями свободы

Уровень значимости, как следует из рис. 1.2, определяется выражением

, (1.36)

где – интегральная функция распределения вероятностей. Доверительный уровень находится по формуле

. (1.37)

Критическая точка

(1.38)

находится по таблицам критических точек или с помощью стандартных функций в пакетах компьютерных программ.

Нулевая гипотеза Н₀: β₁ = β₂ = … = β_р принимается в случае, когда F < F_кр и с уровнем значимости α делается вывод о том, что уравнение регрессии незначимо.

В противном случае, когда F > F_кр, с уровнем значимости α делается вывод о том, что уравнение регрессии значимо.

Величина P-значения составляет

(1.39)

Из рис. 1.2 и сопоставления (1.36), (1.39) следует, что из неравенства P>α вытекает F<F_кр. При этом принимается основная гипотеза H₀. Если же Р<α и F>F_кр, принимается конкурирующая гипотеза Н₁, то есть с уровнем значимости ее делается вывод о том, что уравнение регрессии значимо.

11. Доверительный интервал для значений зависимой переменной

Ошибка регрессионного прогноза составляет

(1.40)

где y_i и – соответственно действительное и предсказанное значения зависимой переменной.

Поскольку и согласно (1.10), (1.11) , где – вектор-строка, представляющий собой i-ю строку (i = 1, 2,…, n) матрицы X объясняющих переменных, ошибка (1.40) имеет нулевое математическое ожидание M[e_i] = 0.

Дисперсия ошибки определяется выражением

(1.41)

В силу того, что второе слагаемое в правой части (1.41) с учетом можно представить в виде

,

а первое слагаемое равно

,

их сумма, представляющая собой величину среднеквадратической ошибки интервального прогноза значений результирующего показателя для некоторого набора значений , определяется выражением

. (1.42)

В итоге посредством замены в (1.42) неизвестного значения σ² на ее оценку получается несмещенная оценка дисперсии индивидуальных значений независимой переменной у_i, соответствующих значениям предикторов

(1.43)

Доверительный интервал для y_i находится по формуле

(1.44)

где ; ; t_кp = t_кp(α; k = n – р – 1)– критическая точка распределения Стьюдента с k = n – р – 1 степенями свободы для уровня значимости α.