7. Анализ вариации зависимой переменной

Общая сумма квадратов отклонений разбивается на два слагаемых

Q = Q_r+Q_e (1.24)

где , – соответственно факторная и остаточная суммы квадратов.

По аналогии со случаем парной регрессии эти суммы можно выразить через вектор выборочных коэффициентов b и выборочный коэффициент детерминации (табл. 1.1)

Таблица 1.1

Значения сумм квадратов

Название	Общее выражение	Выражение через b	Выражение через
Общая
Факторная
Остаточная

При делении суммы квадратов на число ее степеней свободы получается несмещенная оценка соответствующей дисперсии (табл. 1.2).

Таблица 1.2

Значения дисперсий

Название	Df	Выражение
Общая	df = n – 1
Факторная	df = p
Остаточная	df = n – p – 1

8. Выборочный коэффициент детерминации

Выборочный множественный коэффициент детерминации показывает качество подгонки регрессионной модели к наблюдаемым значениям у_i и определяется выражением (в отличие от случая модели парной регрессии он обозначается )

(1.25)

Свойства коэффициента (в дополнение к свойствам для частного случая парной регрессии):

1. Коэффициент служит для оценки значимости (качества) уравнения регрессии, является одной из наиболее эффективных оценок адекватности регрессионной модели, характеристикой ее прогностической силы.

2. Коэффициент при выполнении 5-го условия КЛММР является состоятельной, но смещенной оценкой генерального коэффициента детерминации , с математическим ожиданием и дисперсией, приближенно определяемыми выражениями

;

3. Коэффициент – безразмерная величина, лежащая в пределах 0≤ ≤1.

4. При = 0 вариация зависимой переменной полностью обусловлена воздействием неучтенных в модели переменных и линия регрессии не улучшает качество предсказания значений у_i по сравнению с тривиальным предсказанием (Q_r=0, Q = Q_e).

5. При = 1 осуществляется точная подгонка и все эмпирические точки у_i удовлетворяют уравнению регрессии (Q_r =Q, Q_e=0).

6. Коэффициент может быть вычислен из матрицы парных коэффициентов корреляции по формуле:

(1.26)

где – определитель симметричной квадратной матрицы выборочных парных коэффициентов корреляции (p + 1)-го порядка

с элементами (k, j = 1, 2, ..., р)

; (1.28)

(1.29)

;

Δ₀₀ – алгебраическое дополнение 0-го элемента 0-й строки матрицы (1.27), по сути представляющее собой определитель det R_XX матрицы межфакторной парной корреляции p-го порядка

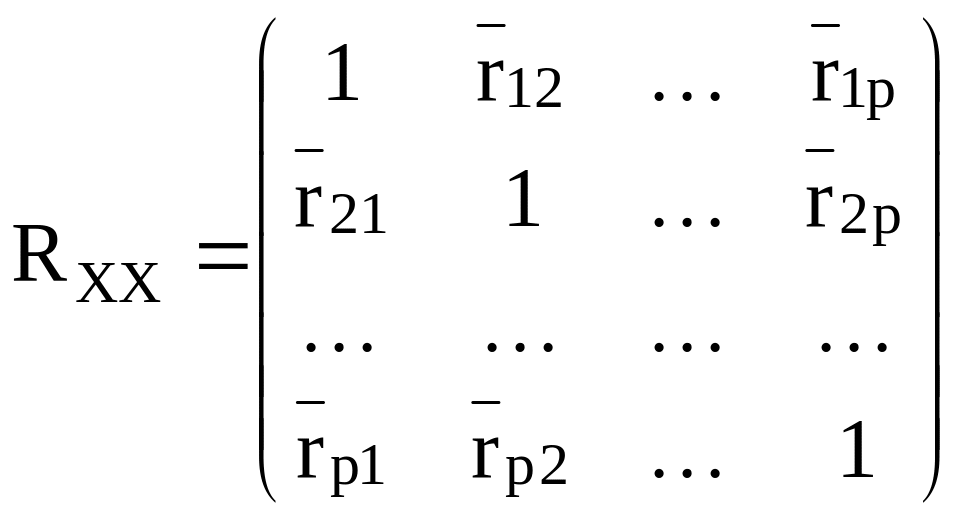. (1.30)

Выражение (1.26) определяет выборочный множественный коэффициент детерминации p-гo порядка (по числу p объясняющих переменных). Множественные коэффициенты детерминации низших порядков определяются аналогичным образом из соответствующих подматриц матрицы R_yX.

Так, выборочный множественный коэффициент детерминации 1-го порядка , равный квадрату парного коэффициента корреляции между результирующей у и j-ой объясняющей переменной x_j, находится по формуле

(1.31)

где – определитель подматрицы , получаемой из матрицы R_yX путем вычеркивания всех строк и столбцов кроме тех, которые соответствуют переменным у и x_j: (первые j-е строка и столбец); Δ₁₁ – алгебраическое дополнение 1-го элемента 1-й строки этой подматрицы. Выборочный множественный коэффициент детерминации 2-го порядка для объясняемой у и факторных переменных x_j, х_k определяется выражением

(1.32)

где – определитель подматрицы _|, которая находится из матрицы R_yX в результате вычеркивания всех строк и столбцов кроме тех, которые отвечают у, x_j и х_k; Δ₁₁ – алгебраическое дополнение 1-го элемента 1-й строки полученной подматрицы.

Выборочные множественные коэффициенты детерминации более высоких порядков находятся аналогичным образом.

7. Величина , вообще говоря, возрастает при добавлении новых регрессоров (поскольку растет Q_r), хотя это не обязательно означает улучшение качества регрессионной модели.

Поскольку присоединение в уравнение регрессии каждой новой предикторной переменной не может уменьшить величины коэффициента детерминации (независимо от порядка присоединения), множественные коэффициенты детерминации различных порядков удовлетворяют цепочке неравенств

(1.33)

Попыткой устранить эффект, связанный с ростом при добавлении новых объясняющих переменных, является коррекция на число регрессоров.