Министерство Образования и Науки Российской Федерации

Новосибирский Государственный Технический Университет

КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ

Курсовой проект по дисциплине

«Численные методы»

Факультет: ПМИ

Группа: ПМ-14

Студент: Полищук С.Ю.

Преподаватель: Персова М.Г.

Вариант: 60

Новосибирск, 2013

Содержание

1. Постановка задачи 2

1.1 Решаемое уравнение 3

1.2 Краевые условия 3

1.3 Расчетная область 3

2. Теоретическая часть 3

2.1 Вариационная постановка 3

2.2 Конечноэлементная дискретизация и переход к локальным матрицам 4

2.3 Схемы численного интегрирования для вычисления локальных матриц 6

3. Описание разработанных программ 6

3.1 Структуры данных 6

3.2 Структура основных модулей программы 7

4. Описание тестирования программ 8

4.1 Тестовые примеры и полученные результаты 8

5. Проведенные исследования и выводы 9

6. Тексты основных модулей программ 10

Листинг программы 10

1. Постановка задачи

МКЭ для двумерной краевой задачи для эллиптического уравнения в полярной системе координат. Базисные функции билинейные на прямоугольниках. Краевые условия всех типов. Коэффициент диффузии разложить по биквадратичным базисным функциям. Матрицу СЛАУ генерировать в разреженном строчном формате. Для решения СЛАУ использовать МСГ или ЛОС с неполной факторизацией.

1.1 Решаемое уравнение

-div( grad )+

задано в некоторой области с границей .

В полярной системе координат:

.

1.2 Краевые условия

, ,

1.3 Расчетная область

Расчётная область разбивается на прямоугольники, содержащие по четыре узла.

Локальная нумерация выглядит следующим образом:

2. Теоретическая часть

2.1 Вариационная постановка

Запишем для исходной краевой задачи эквивалентную вариационную постановку в форме уравнения Галёркина, для этого правую и левую часть исходного уравнения домножим на функцию из пространства пробных функций и проинтегрируем по :

(-div( grad )+ .

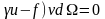
_{Преобразуем полученное уравнение с использованием формулы Грина:}

- .

Воспользовавшись краевыми условиями преобразуем интегралы:

- .

В качестве выберем пространство пробных функций , которые на границе S­₁ удовлетворяют нулевым первым краевым условиям. При этом будем считать, что , где множество функций, имеющих суммируемые с квадратом первые производные и удовлетворяющих только первым краевым условиям на границе S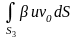₁:

+ + = + + . (1.1)

2.2 Конечноэлементная дискретизация и переход к локальным матрицам

Получим аппроксимацию уравнения (1.1) на конечномерных подпространствах и 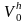, аппроксимирующих исходные пространства и . Для этого заменим функцию аппроксимирующей её функцией , а функцию функцией :

+ + = + + .

Поскольку любая функция может быть представлена в виде линейной комбинации 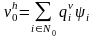, то полученное вариационное уравнение эквивалентно следующей системе уравнений:

+ + = + + .

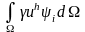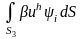Поскольку , оно может быть представлено в виде в итоге получаем СЛАУ для компонент 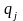вектора весов q с индексами :

= + + .

При решении исходной краевой задачи с использованием базисных функций, принимающих нулевые значения во всех узлах сетки, кроме одного, конечноэлементная СЛАУ для вектора весов q может быть записана в матричном виде: Aq = b, где компоненты матрицы А и вектора b определяются соотношениями

=

= , эти будем интегралы вычислять как сумму интегралов по конечным элементам 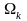, на которые разбита расчётная область:

= = , ,

= = ,

= = , .

В полярных координатах 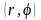примут компоненты локальных матриц вид

= , = .

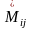Компоненты локального вектора правой части конечного элемента определяются как .

Также формулы эти можно записать в виде .

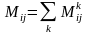Билинейные базисные функции:

На отрезке задаются две одномерные линейные функции

= , = , = .

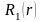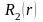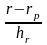Аналогично на интервале задаются линейные функции

= , = , = .

Локальные базисные функции на конечном элементе = представляются в виде произведений:

= , = ,

= , = .

Биквадратичные базисные функции:

= , = , = ,

= , = , = ,

= , = , = .

2.3 Схемы численного интегрирования для вычисления локальных матриц

Для вычисления локальных матриц используется кубатурная формула Гаусса с четырьмя узлами, имеющая четвёртый порядок.

, где

и .

3. Описание разработанных программ

3.1 Структуры данных

На входе программа считывает информацию о сетке и краевых условиях:

Файл g.txt(описывает сетку):

-количество конечных элементов Nr(по r);

-значения всех границ подобластей по r;

-количество конечных элементов Np(по );

-значения всех границ подобластей по ;

-количество подобластей L;

-L наборов по 5 целых чисел, описывающих все подобласти;

-количество узлов N;

-список узлов(номер по r, номер по ).

Файл cond.txt:

-количество рёбер, в которых действуют главные краевые условия n1;

- n1 наборов по 6 целых чисел(тип краевого условия, номер границы, номер элемента по r, с которого рассматриваемый фрагмент границы начинается по оси r, номер элемента по r, которым заканчивается фрагмент по оси r, номер начального элемента по , номер по которым заканчивается фрагмент по оси );

-количество рёбер, в которых действуют вторые краевые условия n2;

-n2 наборов по 6 целых чисел по аналогии с первыми краевыми условиями

-количество рёбер, в которых действуют третьи краевые условия n3;

-n3 наборов по 6 целых чисел.

3.2 Структура основных модулей программы

Программа состоит из четырёх модулей:

-main.cpp(основной модуль, в котором генерируется портрет матрицы, вычисляются локальные матрицы, генерируется глобальная матрица);

-task.h(описывает функцию правой части, коэффициент диффузии , коэффициент , задаются формулы для краевых условий);

-solver.h(решение полученной СЛАУ локально-оптимальной схемой с неполной LU – факторизацией);

-paint.h(визуализация полученного решения и заданной расчётной области).