8.2.2. Относительные величины

Анализируя абсолютные величины, например, статистические данные о торговле, необходимо сопоставлять эти данные во времени и пространстве, исследовать закономерности их изменения и развития, изучать структуру совокупностей. С помощью абсолютных величин эти задачи не выполнимы, в этом случае необходимо использовать относительные величины.

Относительный показатель – это показатель, который представляет собой частное от деления одного абсолютного показателя на другой и дает числовую меру соотношения между ними. В числителе дроби стоит величина, которую сравнивают, а в знаменателе – величина, с которой сравнивают (база сравнения).

Неименованные О.В.

1. Коэффициент получается в том случае, если база сравнения равна 1. Если коэффициент больше 1, то он показывает во сколько раз сравниваемая величина больше, базы сравнения . Если коэффициент меньше 1 , то он показывает какую часть базы сравнения составляет сравниваемая величина .

2. Процент, получатся в том случае, если база сравнения равна 100. Процент получают умножением коэффициента на 100.

3. Промилле (‰) – если база сравнения равна 1000. Получают умножением коэффициента на 1000. Промилле используются для того, чтобы избежать дробных значений показателей. Они широко используются в демографической статистике, где показатели смертности, рождаемости, браков определяются на 1000 человек.

4. Продецимилле (‰0) – если база сравнения равна 10000. Получают умножением коэффициента на 10000. Например, сколько приходится врачей, больничных коек на 10000 человек.

При соотнесении между собой абсолютных величин, данных первичного наблюдения, получившиеся показатели называют относительные показатели первого порядка. Если же необходимо сравнить относительные величины, которые уже являются вторичными (расчетными) показателями, то такие показатели называют относительные показатели второго порядка.

Различают относительные величины динамики, структуры, координации, сравнения и интенсивности, именуемые в дальнейшем индексами.

Относительная величина динамики. Под динамикой в статистике понимается изменения явления во времени. Следовательно, данный вид относительных величин исследует изменения, происходящие в явлении с течением времени. То есть, относительная величина динамики будет представлять собой соотнесение одного и того же показателя по одному и тому же объекту, но в разные периоды времени.

Относительные величины динамики также называют «темпами роста», обозначающимися как «Тр» или индексами. Период, в котором явление принимается за основу для сравнения в статистике принято называть «базисным» и обозначать как « ». Период, в котором происходит сравниваемое явление, называется «отчетным», «текущим» и обозначается как « ». Относительная величина динамики рассчитывается по следующей формуле: 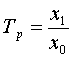или .

Данный показатель показывает изменение явления во времени. Выражается в форме коэффициента – коэффициент роста, и форме процента – темп роста.

Уровень сравниваемого явления может также называться «фактически уровнем», то есть уровнем, фактически достигнутым в отчетном периоде, он имеет обозначение « ». Тогда, относительная величина динамики примет следующий вид:

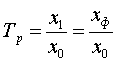
Относительная величина планового задания. В статистике значения признаков исследуемого явления, которые должны быть достигнуты в предстоящем периоде, называются планируемыми значениями.

Относительная величина планового задания (О ) рассчитывается как соотнесение планируемого уровня явления ( ) с уровнем этого же явления, который принимается за основу для сравнения ( ). В качестве базы сравнения принимается фактически достигнутая величина признака исследуемого явления в периоде, который предшествует планируемому, причем не обязательно непосредственное предшествование, за основу для сравнения может приниматься любой предыдущий период. Таким образом, относительная

величина планового задания имеет форму: или

Данный показатель показывает, какое планируется изменение показателя в будущем по сравнению с предшествующем периодом и выражается в процентах.

Относительная величина выполнения плана. Понятие «выполнение плана» подразумевает сравнение планового задания и фактически полученного результата. Следовательно, относительная величина выполнения плана ( ) представляет собой соотнесение фактически достигнутого уровня явления в исследуемом периоде с

планируемым уровнем этого явления: или

.

Данный показатель показывает степень выполнения плана и выражается в форме %.

То есть, данная относительная величина показывает, во сколько раз фактический уровень исследуемого явления в отчетном периоде отличается от запланированного уровня явления на этот период.

Взаимосвязь между относительными величинами динамики, планового задания, выполнения плана.

При наличии планируемого уровня в построении относительных величин, отражающих изменения явления во времени, анализу подвергаются три уровня: базисный, планируемый и фактический. Последовательный расчет изменения сначала планируемой величины относительно базисной, затем фактической величины относительно планируемой позволяет судить об изменении явления за исследуемый период в целом, т.е. изменении фактического уровня относительно базисного или характеризует относительную величину динамики:

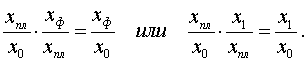
Таким образом, произведение относительных величин планового задания и выполнения плана равно относительной величине динамики взаимосвязь между показателями: .

Данное выражение отображает взаимосвязь относительных величин планового задания, выполнения плана и динамики.

Относительные показатели, характеризующие структуру объекта.

Под структурой в статистике понимаются сведения о делении исследуемой совокупности на отдельные группы, о величине каждой из групп и об их значении для совокупности в целом. Поэтому относительная величина структуры (d) в статистике представляет собой соотнесение части явления (f) и явления в целом (суммы всех частей, f):

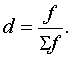или относительный показатель структуры:

.

Данный показатель рассчитывается по группированным данным и показывает долю отдельных частей в общем объеме совокупности. Может выражаться в форме коэффициента (доли) или процента (удельные веса). Пример, 0,4 – доля, 40% - удельный вес. Сумма всех долей равна 1, а удельных весов 100%.

То есть относительная величина структуры показывает, какую долю (или сколько процентов) составляет часть совокупности в общем объеме совокупности. Синонимом понятия «относительная величина структуры» являются также понятия «удельный вес», «доля».

Необходимо отметить особенность данных, для которых может рассчитываться относительная величина структуры: данные должны быть сгруппированы, то есть пройти первичную обработку после наблюдения.

Расчет изменения относительной величины структуры во времени.

Для полноценного анализа недостаточно исследовать только структуру явления, необходимо сопоставить распределение явления по группам в изучаемом периоде с распределением, существовавшим в предыдущих периодах. Построение относительных величин структуры явления для нескольких периодов позволяет выявить изменения в структуре явления, происходящие в течение времени. Такие изменения в статистике называют «структурными сдвигами».

Расчет структурных изменений явления во времени

( )

определяется соотношением изменения части явления во времени ( ) с изменением во времени явления в целом ( ): .

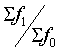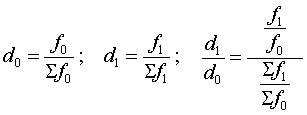Относительная величина координации.

Относительная величина координации характеризует соотношение частей целого между собой. То есть, помимо определения удельного веса различных частей сравнительно со всей совокупностью, применяются также относительные величины, отражающие сравнение различных частей друг с другом.

Относительная величина координации (ОВК) имеет форму, опирающуюся на ее сущность – сравнение одной части исследуемой совокупности ( ) с другой частью этой же

совокупности ( ): 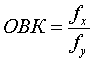или относительный показатель координации:

.

Величина показывает сколько единиц сравниваемой части приходится на 1, 10, 100 или 1000 единиц части, принятой за основу для сравнения. Например, сколько женщин приходится на 1000 мужчин.

Относительная величина сравнения. Относительная величина сравнения отражает соотнесение показателей, имеющих одинаковые содержание, единицы измерения, период или момент времени, но рассчитанные для разных объектов. То есть данную относительную величину выделяют в отдельный вид, т.к. она позволяет сопоставлять различные объекты по изучаемым признакам. Форма относительной величины сравнения (ОВС) обусловлена ее содержанием: соотнесение определенной характеристики объекта А ( ) с такой же характеристикой объекта В за тот же период ( ):

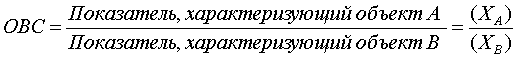
В качестве примера расчета относительных величин сравнения можно привести следующие показатели:

1) соотношение объемов добычи нефти за 1999 год в США с объемами добычи нефти за 1999 год в РФ,

2) сопоставление среднегодового размера внутреннего валового продукта, приходящегося на душу населения в Германии за период с 1995 по 2000 г.г., со среднегодовым размером внутреннего валового продукта, приходящегося на душу населения в Российской Федерации за этот же период; и т.д.

Относительная величина интенсивности. Под интенсивностью понимается частота появления явления. Относительные величины интенсивности (ОВИ) отражают степень распространенности явления:

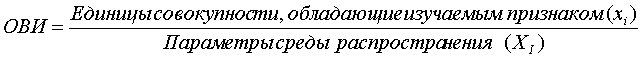
Приведем пример относительных величин интенсивности:

1) соотношение производственных и энергетических мощностей предприятия с численностью рабочих, использующих эти производственные мощности для создания продукции предприятия;

2) соотнесение удвоенного количества перевезенного груза (ввиду двойной обработки, которой подвергается груз сначала при погрузке, затем при выгрузке), к числу судо-суток стоянки судов в портах под грузовыми операциями покажет интенсивность грузовых работ в портах (или скорость обработки транспортных судов в портах); и т.д.

Необходимо подчеркнуть, что относительные величины интенсивности всегда являются результатом соотношения показателей, различных по содержанию, единицам измерения, но одинаковым по временному периоду изучения. В этом и состоит их отличие от других относительных величин, например, относительных величин сравнения. Кроме того, относительные величины интенсивности всегда именованные, то есть выражаются не в процентах, или количестве раз изменения исследуемого явления, принадлежащего различным объектам, а в определенных величинах, зависящих от содержания показателя. В приведенных выше примерах относительных величин интенсивности единицами измерения соответственно будут:

1) объем производственных мощностей на одного рабочего;

2) количество груза за судо-сутки стоянки в портах.