1.6.3 Методика изучение стохастических зависимостей в случае множественной корреляции
Методика проведения корреляционно – регрессионного анализа в случае множественной корреляции состоит из следующих этапов: спецификация, параметризация, верификация и практическое использование модели.
Спецификация модели
При построении регрессионных моделей важное значение имеет выбор независимых (факторных) переменных для предсказания значений результативного показателя. Общего алгоритма такого выбора не существует.
При отборе следует придерживаться определенных правил:
между факторными и результативным показателями должна существовать значимая причинно-следственная связь;
не рекомендуется включать в расчет взаимосвязанные факторные показатели (если коэффициент парной линейной корреляции больше 0,85, то один из факторов надо исключить).
Для оценивания зависимости между показателями рассчитывают различные коэффициенты корреляции. В уравнение регрессии следует включать только те факторные переменные, связь которых с результативным признаком, является статистически значимой (проверяется по критерию Стьюденту).
Для определения вида зависимости между факторными и результативным показателями следует использовать теоретические зависимости той отрасли знаний, к которой относятся исследуемые явления. В качестве вспомогательного инструмента при определении вида зависимости можно использовать попарные диаграммы разброса между результативной и факторной переменными.
Параметризация модели
Для оценивания параметров модели используют метод наименьших квадратов. На практике для определения коэффициентов используют специальные компьютерные программы (например, Пакет анализа MS Excel, EViews и другие).
Верификация модели
Оценка качества построенной модели аналогична случаю парной корреляции.
Если коэффициент
при соответствующей переменной
является статистически незначимым, то
данная переменная, возможно, включена
в модель ошибочно и ее следует исключить
из уравнения. При исключении из уравнения
переменных, следует придерживаться
следующего алгоритма.
1.
Исходную модель, которая включает все
переменные, назовем моделью без
ограничений. Коэффициент детерминации
данной модели обозначим
.
2.
Оценивается модель, в которой исключены
незначимые переменные. Назовем эту
модель моделью с ограничениями. Для нее
определяют коэффициент детерминации
.
Коэффициент детерминации
всегда меньше, чем коэффициент детерминации
в исходной модели.
3. Если коэффициент детерминации существенно не отличается от коэффициента детерминации , то выбор следует сделать в пользу модели с ограничениями.
Для
ответа на вопрос, какое различие между
коэффициентами детерминации считать
существенным, необходимо проверить
гипотезы:
.
Если справедлива гипотеза , то выбор делают в пользу модели с ограничениями. Если справедлива гипотеза , то выбор делают в пользу исходной модели.
Для проверки используют статистику
,
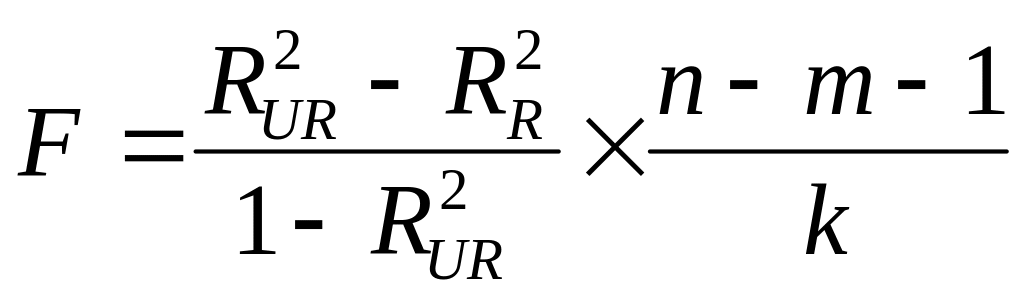которая имеет F-
распределение с числом степеней свободы
и
.
Здесь
- количество исключенных незначимых
переменных.
Интерпретация моделей регрессий осуществляется методами той отрасли знаний, к которой относятся исследуемые явления.
Коэффициент
показывает, на сколько единиц изменится
зависимая переменная Y
при изменении переменной
на единицу собственного измерения.
С целью расширения возможностей анализа
и интерпретации регрессионных моделей
можно рассчитать коэффициенты
эластичности, определяемые по
формуле:
,
где
- среднее значение соответствующей
объясняющей переменной
,
‑ среднее значение зависимой переменной
Y,
‑ коэффициент уравнения регрессии
при соответствующей переменной
.
Чтобы оценить какая из объясняющих
переменных
оказывает большее влияние на изменение
переменной Y, рассчитывают
стандартизованные коэффициенты
регрессии:
, где
-
стандартное отклонение переменной
,
-
стандартное отклонение переменной Y.
Стандартизованный коэффициент регрессии показывает, на сколько стандартных отклонений изменится переменная Y при изменении переменной на одно стандартное отклонение. По величине стандартизованных коэффициентов можно сравнивать степень влияния объясняющих переменных на изменение зависимой переменной.
Практическое применение уравнения регрессии.
Уравнение регрессии можно использовать для следующих целей:
расчета влияния факторов на результативный показатель:
;
подсчета резервов повышения (понижения) уровня исследуемого показателя:
,
где
;
планирования и прогнозирования значений результативного показателя. С этой целью в конечное уравнение связи подставляют возможные значения факторных показателей.