Пример выполнения задания на тему «изгиб с кручением»
Для стального вала постоянного поперечного
сечения с двумя зубчатыми колесами (
рис. 5.1,а ), передающего мощность Р = 15
кВт при угловой скорости
,
определить диаметр вала по двум вариантам:
а) используя третью гипотезу прочности;
б) используя пятую гипотезу прочности.
Принять:
;
;
.
Решение:
1. Составляем расчетную схему вала, приводя действующие на вал нагрузки к оси (рис. 5.1, б). При равномерном вращении вала М1 = М2, где М1 и М2 - скручивающие пары, которые добавляются при переносе сил F1 и F2 на ось вала.
2. Определяем вращающий момент, действующий на вал:
.
3. Вычислим нагрузки, приложенные к валу:
;
;
;
.
4. Определяем реакции опор в вертикальной плоскости (рис. 5.1, б):
;
;
;
;
.
,
следовательно,
,
и
найдены правильно.
Определяем реакции опор в горизонтальной плоскости (рис. 5.1, б):
.
Знак минус указывает, на то, что истинное направление реакции противоположно выбранному:
,
следовательно,
и
найдены верно.
5. Строим эпюру крутящих моментов
(рис. 5.1,в).
6. Определяем в характерных сечениях
значения изгибающих моментов
в вертикальной плоскости и
в горизонтальной плоскости и строим
эпюры (рис. 5.1, г, д):
;
;
;
.
7. Вычисляем наибольшее значение эквивалентного момента по заданным гипотезам прочности. Так как в данном примере значение суммарного изгибающего момента в сечении С больше, чем в сечении D,
;
,
то сечение С и является опасным. Определяем эквивалентный момент в сечении С.
Вариант а:
.
Вариант б:
8. Определяем требуемые размеры вала по вариантам а и б.
По варианту а
.
По варианту б
Принимаем
.
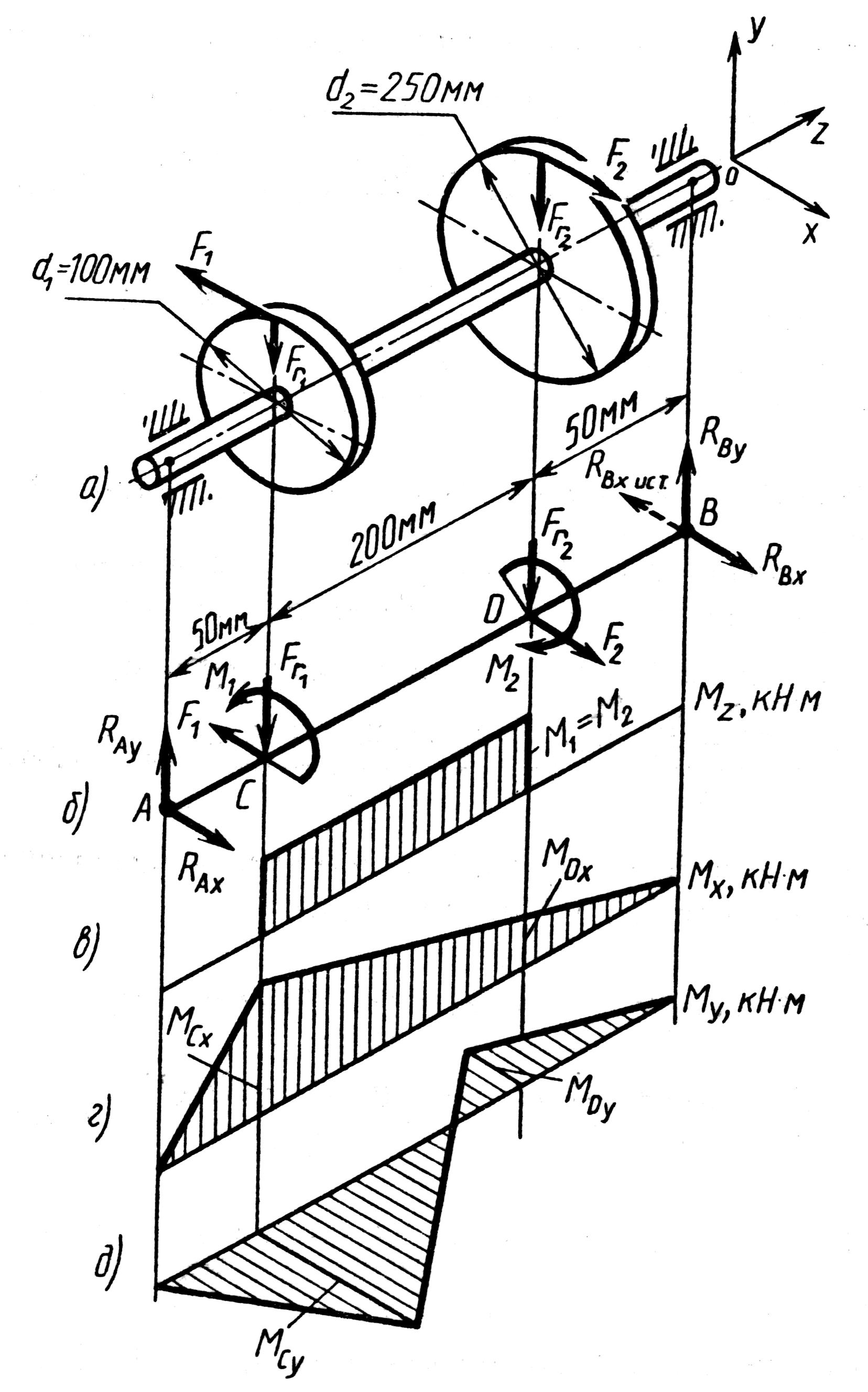
Рисунок 5.1
6. Варианты заданий задача 1. «растяжение – сжатие»
1. Построить по длине бруса, согласно схеме нагружения, эпюры продольных сил N, нормальных напряжений s и перемещений поперечных сечений.
2. Сделать вывод о прочности бруса, сравнив значение нормальных напряжений в опасном сечении с допустимым (материал бруса: сталь 3, Е=2,1×105 МПа, [s] =240 МПа,). Если smax<[s], определить степень загруженности бруса, если smax[s], то необходимо подобрать требуемые площади поперечных сечений S1 или S2 (по известным продольным силам N и допускаемому напряжению [s] ).
3. Найти допустимое значение продольной силы [N] для обеих ступеней бруса с площадями S1 и S2.
Таблица 6.1 Варианты заданий к задаче 1.
-
Вариант задания
(предпоследняя
цифра шифра)
Значение сосредоточенной нагрузки. кН
Площадь сечения, мм2
Длина участка,
м
F1
F2
F3
S1
S2
a
b
0
16
15
10
200
120
0.2
0.4
1
15
14
9
180
110
0.1
0.5
2
14
16
11
220
100
0.3
0.6
3
17
13
8
170
100
0.2
0.4
4
30
10
20
300
200
0.3
0.2
5
28
12
22
320
180
0.6
0.4
6
32
14
21
280
210
0.3
0.3
7
10
12
30
200
300
0.3
0.4
8
12
8
28
190
310
0.3
0.6
9
40
42
20
300
200
0.3
0.2
Схемы нагружения к задаче 1 (последняя цифра шифра).
ЗАДАЧА 2. «ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК ПЛОСКОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ»
Определить положение главных центральных осей и вычислить величины главных центральных моментов инерции сложного составного сечения.
Для решения задачи требуется:
Вычертить в масштабе всё сечение. При вычерчивании элементы сечения располагать вплотную один к другому.
Определить положение центра тяжести всего сечения.
Вычислить осевые и центробежный моменты инерции относительно произвольных центральных осей (осей, проходящих через центр тяжести сечения, параллельно выбранной системе декартовых координат).
Определить теоретически положение главных осей инерции.
Вычислить значения главных моментов инерции.
Показать на чертеже положение главных осей инерции.
Данные к задаче следует взять лишь тех профилей проката, которые входят в заданную схему.
Таблица 6.2 Варианты заданий к задаче 2
-
Предпоследняя цифра шифра
Равнополочный уголок
Вертикальная полоса
Горизонтальная полоса
Двутавр, №
Швеллер, №
1
90×90×9
500×10
400×10
24
16
2
100×100×10
500×12
400×10
24
16
3
100×100×12
500×12
400×12
27
18
4
110×110×8
600×10
400×12
30
18
5
125×125×12
400×10
400×12
22
18
6
140×140×10
500×12
500×10
24
20
7
140×140×12
600×12
500×10
27
20
8
160×160×12
600×16
600×10
30
22
9
180×180×12
600×20
500×12
40
24
0
100×100×8
500×10
400×10
36
22
Схема сечения к задаче 2 (последняя цифра шифра).
