1.3. Выявление тенденции в изменении урожайности подсолнечника.

В ходе обработки динамического ряда важнейшей задачей является выявление основной тенденции развития явления (тренда) и сглаживание случайных колебаний. Для решения этой задачи в статистике существуют особые способы, которые называют методами выравнивания.

Выделяют три основных способа обработки динамического ряда:

а) укрупнение интервалов динамического ряда и расчет средних для каждого укрупненного интервала;

б) метод скользящей средней;

в) аналитическое выравнивание (выравнивание по аналитическим формулам).

Укрупнение интервалов - наиболее простой способ. Он заключается в преобразовании первоначальных рядов динамики в более крупные по продолжительности временных периодов, что позволяет более четко выявить действие основной тенденции (основных факторов) изменения уровней.

По интервальным рядам итоги исчисляются путем простого суммирования уровней первоначальных рядов. Для других случаев расcчитывают средние величины укрупненных рядов (переменная средняя). Переменная средняя рассчитывается по формулам простой средней арифметической.

Скользящая средняя - это такая динамическая средняя, которая последовательно рассчитывается при передвижении на один интервал при заданной продолжительности периода. Если, предположим, продолжительность периода равна 3, то скользящие средние рассчитываются следующим образом:

   

При четных периодах скользящей средней можно центрировать данные, т.е. определять среднюю из найденных средних. К примеру, если скользящая исчисляется с продолжительностью периода, равной 2, то центрированные средние можно определить так:

   

Первую рассчитанную центрированную относят ко второму периоду, вторую - к третьему, третью - к четвертому и т.д. По сравнению с фактическим сглаженный ряд становится короче на (m - 1)/2, где m - число уровней интервала.

Важнейшим способом количественного выражения общей тенденции изменения уровней динамического ряда является аналитическое выравнивание ряда динамики, которое позволяет получить описание плавной линии развития ряда. При этом эмпирические уровни заменяются уровнями, которые рассчитываются на основе определенной кривой, где уравнение рассматривается как функция времени. Вид уравнения зависит от конкретного характера динамики развития. Его можно определить как теоретически, так и практически. Теоретический анализ основывается на рассчитанных показателях динамики. Практический анализ - на исследовании линейной диаграммы.

Задачей аналитического выравнивания является определение не только общей тенденции развития явления, но и некоторых недостающих значений как внутри периода, так и за его пределами. Способ определения неизвестных значений внутри динамического ряда называют интерполяцией. Эти неизвестные значения можно определить:

1) используя полусумму уровней, расположенных рядом с интерполируемыми;

2) по среднему абсолютному приросту;

3) по темпу роста.

Таблица 1.3 - Выравнивание динамического ряда урожайности подсолнечника в Воронежской области, ц

Годы	Урожайность	Укрупнение периодов времени		Скользящая средняя
		сумма по трехлетиям	средняя за трехлетие	сумма по трехлетиям	средняя за трехлетие
2003	11,4
2004	9,8	33,5	11,2	33,5	11,2
2005	12,3			34,0	11,3
2006	11,9			39,2	13,1
2007	15,0	42,9	14,3	42,9	14,3
2008	16,0			46,4	15,5
2009	15,4			38,6	12,9
2010	7,2	43,4	14,5	43,4	14,5
2011	20,8

Выравнивание динамики с помощью метода укрупнения периодов времени показало, что урожайность за 3 трехлетних периода возрастала с 11,2ц/га до 14,5ц/га, то есть наблюдается тенденция роста урожайности. Выравнивание динамики с помощью метода скользящей средней показало, что урожайность за 5 трехлетних периода возрастала с 11, 2 ц/га до 15,5 ц/га, затес с 2008-2010 гг. уменьшилась на 2,6 ц/га и за последний трехлетний период увеличилась на 1,6 ц/га.

Таблица 6 - Аналитическое выравнивание урожайности подсолнечника

Годы	Урожайность, (ц/га) (у)	Условное значение периода времени (t)	t2	y*t	Выравненная урожайность ряда yt=a0+a1t
2003	11,4	-4	16	-45,6	10,5
2004	9,8	-3	9	-29,4	11,2
2005	12,3	-2	4	-24,6	11,9
2006	11,9	-1	1	-11,9	12,6
2007	15,0	0	0	0	13,3
2008	16,0	1	1	16,0	14,0
2009	15,4	2	4	30,8	14,7
2010	7,2	2	9	21,6	15,4
2011	20,8	4	16	83,2	16,1
Итого:	119,8	0	60	40,1	119,7

Подставим итоговые данные таблицы в систему уравнений:

9* a₀+ a₁*0=119,8;

a₀*0+60* a₁=40,1;

9* a₀=119,8;

60* a₁=40,1;

a₀=13,3;

a₁=0,7.

Подставим найденные значения параметров a₀ и a₁ в уравнение прямой и найдём его конкретное выражение:

y_t=13,3+0,7*t

Параметр a₁ – свидетельствует о том, что ежегодно в течение изучаемого периода урожайность подсолнечника повышалась на 0,7 ц/га. Аналитическое выравнивание показало, что с 2003 по 2011 гг. урожайность достигла значения 16,1ц/га. Таким образом, получен выравненный ряд урожайности подсолнечника, который говорит о ее систематическом росте с годовым приращением в 0,7ц/га.

Представим полученные данные по выравненным рядам динамики графически:

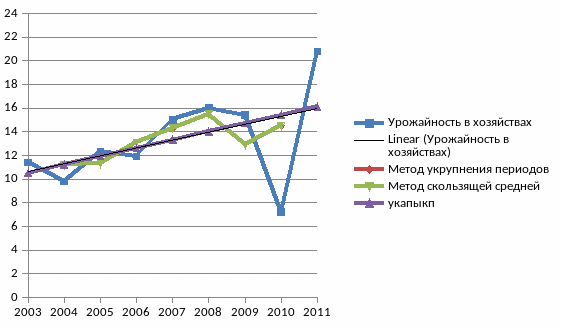
Рис. 2 - Выравнивание динамики урожайности подсолнечника

Ниже рассмотрим расчет показателей вариации подсолнечника в Воронежской области за последние 9 лет.

С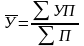 редняя урожайность рассчитывается по формуле средней арифметической взвешенной:

;

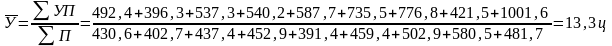
Размах вариации – это разность между максимальным и минимальным значением признака:

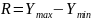
R = 20,8 ц/га – 7,2 ц/га = 13,6 ц/га;

Дисперсия представляет собой средний квадрат отклонений значений признака от его среднего значения:

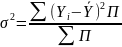
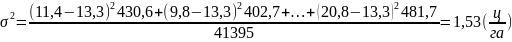
Среднеквадратическое отклонение представляет корень квадратный из дисперсии:

;

;

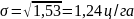Коэффициент вариации определяется как отношение среднеквадратического отклонения к средней величине в процентах:

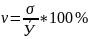
На основе рассчитанных показателей вариации можно сделать вывод:

Размах вариации составляет 13,6 ц/га, то есть (20,8-7,2) свидетельствует о значительных различиях в условиях формирования урожайности.

Отклонения от средней урожайности также большие и достигают -6,1 ц/га и +7,5 ц/га, то есть в 2010 году урожайность ниже среднего уровня на 6,11 ц/га, а в 2011 г. выше на 7,5 ц/га.

Соотношение случайных индивидуальных и общих условий находят отражение в коэффициенте вариации. 𝝂=9,3 %, следовательно, влияние случайных и индивидуальных условий составляет 9,3 % по отношению к влиянию общих условий, формирующих средний уровень, приравненный к 100%. В нормально распределенной совокупности единиц коэффициент вариации может составлять до 33 %. Так как коэффициент вариации урожайности подсолнечника в Воронежской области меньше 33%, то среднюю урожайность равную 13,3 ц/га можно считать типичной, обобщающей характеристикой исследуемой совокупности, которая является однородной.

Фактическая урожайность подсолнечника с 2003 по 2011 гг. отклоняется от средней урожайности =13,3 ц/га на среднеквадратическое отклонение (σ=±1,24 ц/га).