2.Секвенциальные равновесия и равновесия Нэша.

Интуитивно ясно, что понятие секвенциального равновесия является усилением понятия равно­весия по Нэшу. Во всяком случае, мы видели в примере, что не всякое равно­весие Нэша может быть поддержано системой вер до секвенциального.

Скажем точнее. Пусть а - профиль поведенческих стратегий, образующий равновесие Нэша. Тогда правило Байеса однозначно определяет веры f_i(h) в тех информационных множествах, которые достижимы (при стратегиях а) с положительной вероятностью (лежат на пути игры). Тогда стратегии, а секвенциально рациональны в таких информационных множествах и при таких верах. В самом деле, в противном случае игрок, делающий ход в h₇ мог бы получить больший (условный, в ’’подыгре”, начинающейся в К) выигрыш, изменив стратегии в этой подыгре.

Обратно, пусть а - профиль поведенческих стратегий, секвенциально раци­ональных в информационных множествах, лежащих на пути игры. Мы утвер­ждаем, что а - равновесие Нэша. В самом деле, представим, что некоторый игрок / может улучшить результат, применив альтернативную стратегию е'. Но тогда он должен сыграть лучше сг* в некотором своем информационном множестве h. Нужно взять самое первое такое множество; так как до него стратегии не менялись, то не менялись и веры. Но в таком случае стратегия Oi была не секвенциально рациональной в этом h.

Теорема. Профиль поведенческих стратегии, а является равновесием Нэша тогда и только тогда., когда найдется такая система вер f_i, что:

(1) система fi слабо согласована с профилем а;

(2) профиль а секвенциально рационален (при верах n) во всех информа­ционных множествах, лежащих на пути игры.

Отсюда можно сделать два важных вывода. Первый - вдоль пути игры (где веры однозначно определяются правилом Байеса) равновесные страте­гии секвенциально рациональны. Второй - секвенциальная рациональность усиливает равновесность (по Нэшу) тем, что требует секвенциальную рацио­нальность не только вдоль равновесного пути, но и во всех остальных инфор­мационных множествах. Этим она сближается с требованием совершенства относительно подыгр. И действительно, из приведенного выше предложения легко получить, что любое секвенциальное равновесие совершенно к подыграм.

3.Сильное секвенциальное равновесие.

В сильном секвенциальном равновесии мы более строго подходим к формированию вер в информационных множествах, лежащих вне пути игры. Рассмотрим пример, апеллирующий к структурной состоятельности. Пусть игра имеет вил

И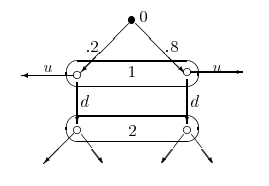 пусть первый играет и. Каковы могут быть веры у 2-го? Так как 1-й не различа­ет эти состояния (правое и левое), он и отклоняться в них должен одинаково. Поэтому естественно считать, что веры 2-го - это .2 и .8.

Дадим теперь общее определение сильной согласованности вер со стратегиями. Пове­денческий профиль о называется вполне смешанным, если любая позиция достигается с положительной вероятностью. В этом случае правило Байеса однозначно определяет согласованную с а систему вер ц(а).

Определение. Система вер ц называется сильно согласованной с профилем стратегий а, если существует последовательность вполне смешанных стратегических профилей а_п, такая что о_п сходится к а, а. соответствующие веры ц,_п = ц,{о_п) сходятся к ц„

Секвенциальное равновесие - это пара (а, ц), что ц сильно согласована с а, а, а секвен­циально рациональна относительно ц„

С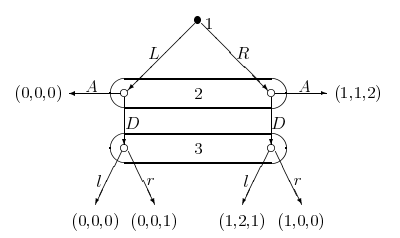 ледующий пример демонстрирует слабое секвенциальное равновесие, которое не силь­ное секвенциальное. Пусть третий игрок верит, что реализуется левая вершина в его информационном мно­жестве. Такая вера вместе со стратегиями (R, А, г) является слабым секвенциальным рав­новесием. Однако оно не является сильным секвенциальным равновесием, потому что вера третьего, сильно согласованная со стратегиями R и А, указывает на правую вершину в информационном множестве 3. Сильным секвенциальным равновесием (единственным?) здесь будет (И. I). /).

Теорема. Любая конечная игра имеет сильное секвенциальное равновесия.

Отметим также, что даже сильные секвенциальное равновесия не всегда исключают слабо доминирующие стратегии.