Вопросы для самоконтроля:

1. Дайте определение равновесия Нэша?

2. Приведите примеры таких равновесий?

3. Сформулируйте теорему Нэша?

Список литературы

Основная:

1. Оуэн Г. Теория игр. Учебное пособие. Санкт-Петербург: ЛКИ, 2008 – 229 с.

2. Губко М.В., Новиков Д.А Теория игр в управлении организационными процессами [Электронный ресурс]: Учебное пособие. М.: Наука, 2005 – 138 с.

3. Даниловцева Е.Р., Теория игр: основные понятия: текст лекций [Электронный ресурс]. Санкт-Петербург: СПбГУАП, 2003 – 36 с.

4. Коковин С.Г., Лекции по теории игр [Электронный ресурс]. Новосибирск: Типография НГУ, 2010 г. – 91 с.

Дополнительная:

1. Самаров К.Л. Элементы теории игр [Электронный ресурс]. Учебное пособие. Новосибирск: Типография НГУ, 2010 г. – 91 с.

2. Саакян Г.Р. Лекции. Теория игр [Текст] : электронный учебник/ Г.Р. Саакян .- Шахты, 2006.

Лекция № 18. Секвенциальные равновесия

Цель: изучить понятие секвенциальные равновесия, рассмотреть основные особенности игр с таким равновесием.

Ключевые слова: секвенциальное равновесие, равновесие Нэша.

Вопросы:

1. Слабое секвенциальное равновесие.

2. Слабое секвенциальное равновесие и равновесие Нэша.

3. Сильное секвенциальное равновесие.

1.Слабое секвенциальное равновесие.

Понятие совершенства равновесия по отноше­нию к подыграм дает мощный принцип отсеивания ’’плохих” равновесий. Од­нако он плохо работает, если в игре мало подыгр. Это можно продемонстри­ровать на следующей модификации предыдущего примера.

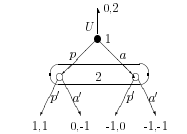Рассмотрим один пример: В ней имеется равновесие (D, a, L). Это равновесие совершенно, но только потому, что здесь нет собственных подыгр. Однако выбор вторым игроком стратегии, а странен. Ведь если он уверен, что 3-й будет использовать L. то ему надо было бы выбрать d. Пусть даже шанс сделать ход для 2-го ничтожен, но d лучше а! И если он выберет d₇ то 1-й переключится па Л, а тогда 3-й переключится на R. Но тогда 2-й вернется к а, 1-й останется на А, и это дает второе равновесие (A, a, R).

Здесь нет подыгр, и буква определения молчит, но дух совершенства тре­бует определенно и ясно: игрок в любой позиции должен действовать оптимально, даже если маловероятно, что удастся попасть в эту позицию. Как же придать этому смысл?

Как уже было сказано, секвен­циальное равновесие состоит из данных двух типов - стратегий и вер. Бо­лее формально, профиль (поведенческих) стратегий образует семейство а = , h Н₇ где h пробегает множество Н информационных множеств на­шей развернутой игры, a ah £ A(M(h)) (напомним, что M(h) - множество ходов или акций, доступных в информационном множестве К). Системой вер называется семейство ц = (//(/г), h £ Н), где ц(К) £ А {К).

Ч тобы быть секвенциальным равновесием, пара (т,) должна удовлетво­рять двум условиям вроде а) и б). Первое условие требует рациональность поведения каждого игрока в каждом ’’своем” информационном множестве. Предположим, что дано информационное множество /го, контролируемое иг­роком io? ^и некоторая вера £ Д(/го). Пусть также задан некоторый про­филь поведенческих стратегий а = (сг).

Скажем, что игрок го секвенциально рационален в информационном множестве /го при вере //о, если, при фиксированных стратеги­ях остальных игроков, ожидаемый при вере цо выигрыш игрока го в подыгpe G(ho), начинающейся в /го, достигает максимума именно на стратегии (a_h, h £ Щ).

Фактически, при фиксации стратегий остальных, наша игра превращается в игру одного лица. Требуется, чтобы в подыгре G(ho) игрок го вел себя оптимально. Отметим, что реальное ограничение здесь накладывают только f_i(h₀) и смешанные ходы нашего игрока в информационных множествах /г, расположенных после ho.

Например, в игре ’’ослик Селтена” стратегический профиль (D, a, L) усло­вию рациональности в вершине 2 не удовлетворяет: если 2-й игрок считает, что 3-й играет L, то он выберет d₇ а не а.

Профиль стратегий, а называется секвенциально рацио­нальным относительно системы вер х, если каждый игрок секвенциально рационален во всех своих информационных множествах h.

Второе условие (уже на веры) требует, чтобы веры ц были не произвольны, но оправдывались ’’более ранним” поведением а хотя бы в следующем "слабом” смысле. Если информационное множество h достигается (при профиле стратегий а) с положительной вероятностью, то вера f_i(h) должна вычис­ляться по правилу Байеса. Если же информационное множество h лежит вне пути игры, вера f_i(h) может быть произвольной. Будем говорить в этом случае, что веры слабо согласованы со стратегиями. Грубо говоря, вера не должна противоречить наблюдениям за ходом игры.

Такой набор (т, fi) называется слабым секвенциальным равновесием. По существу это понятие (в сильном варианте) было введено Крепсом и Уилсо­ном в 1982 г. Отметим, что условие на веру f_i(h) в информационном множе­стве h накладывают только смешанные ходы в множествах h', располо­женных ранее h.